2023数字中国创新大赛网络数据安全赛道决赛WP(1)
比赛感想
不多说了,还是菜,各种不会,还得学
数据安全题目
Crypto-ddddmm
import os
from Crypto.Util.number import *
from secret import flag
def genkey(bits):
p = getPrime(bits)
q = getPrime(bits)
while (p-1) % 7 == 0 or (q-1) % 7 == 0:
p = getPrime(bits)
q = getPrime(bits)
n = p * q
e = 0x10001
d = inverse(e, (p-1)*(q-1))
return (e, n), (p, q, d)
def flip_bit(num, idx):
return num ^ (1 << idx)
def signature(m, sk):
p, q, d = sk
sig = pow(m, d, p*q)
return sig
def fault_signature(m, sk, flip_idx):
p, q, d = sk
dd = flip_bit(d, flip_idx)
sig = pow(m, dd, p*q)
return sig
def pad(msg, length):
pad_length = length - len(msg) - 1
pad_data = os.urandom(pad_length)
return msg + b'\x00' + pad_data
def unpad(msg):
return msg.split(b"\x00")[0]
bits = 512
pk1, sk1 = genkey(bits)
e1, n = pk1
p, q, d1 = sk1
e2 = 7
d2 = inverse(e2, (p-1)*(q-1))
pk2 = (e2, n)
sk2 = (p, q, d2)
m = bytes_to_long(pad(flag, bits//4-1))
msg = bytes_to_long(b'ddddhm')
c = pow(m, e1, n)
msg_sig = signature(msg, sk2)
msg_fault_sigs = []
for idx in range(0, d2.bit_length()*2//3):
fault_sig = fault_signature(msg, sk2, idx)
msg_fault_sigs.append(fault_sig)
print(f'n = {n}')
print(f'd2_nbits = {d2.bit_length()}')
print(f'c = {c}')
print(f'msg_sig = {msg_sig}')
print(f'msg_fault_sigs = {msg_fault_sigs}')
本题的关键在于fault_signature函数。注意到在该函数中,每次进行加密使用的d是由d2变化得来的,且每次仅变化1位。由于d2肯定是奇数,所以第一次变换时,使用的结果肯定是d2-1,即
msg_fault_sigs[0] = pow(msg, d2-1, n)
接下来看下一位。下一位我们不知道是0还是1,但是如果这一位是0,参与计算的就是d2+2;如果这一位是1,参与计算的就是d2-2。由于我们知道pow(msg, d2-1, n),所以可以通过这个值来验证这一位的结果是否为pow(msg, d2-2, n),即这一位是否为1。同理,对于其他位置,都可以如此处理,最终可以得到d2的尾部内容。代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Crypto.Util.number import *
n = 129796898134024157099156452709058687368221438176030502692200747714575571701027659861801365516981802018997712595009646737912670988500232545577601552315965176230630625733276337162755295073834150653688782811860047196091202071789102378530279205691266477048001888471022116120453815115157747843722970514365474705361
msg_sig = 45588026639453540614209700278011089411155941366441867967608269376572773649222458505929678835171063978513562524842704550251413928579096289510261727050687647392547776693337400122310176000901151825994980601875289096262412881003000600445821033469228193081998689326645879888998639588132546327028023877114420047558
msg_fault_sigs = [...]
msg = bytes_to_long('ddddhm')
pows = 2
part_d = "1"
for i in range(1, len(msg_fault_sigs)):
if((msg_fault_sigs[i] * pow(msg, pows-1, n) - msg_fault_sigs[0]) % n)==0:
part_d = "1" + part_d
else:
part_d = "0" + part_d
pows *= 2
part_d = int(part_d, 2)
print part_d.bit_length()
print part_d
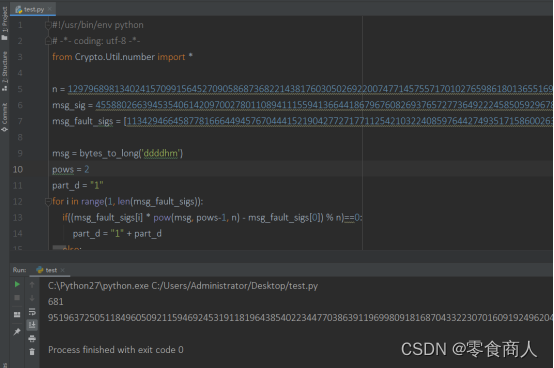
这样得到了d2的后681位。而d2本身只有1024位,所以可以使用coppersmith求解p。
from sage.all import *
def partial_p(p0, kbits, n):
PR.<x> = PolynomialRing(Zmod(n))
nbits = n.nbits()
f = 2^kbits*x + p0
f = f.monic()
roots = f.small_roots(X=2^(nbits//2-kbits), beta=0.3) # find root < 2^(nbits//2-kbits) with factor >= n^0.3
if roots:
x0 = roots[0]
p = gcd(2^kbits*x0 + p0, n)
return ZZ(p)
def find_p(d0, kbits, e, n):
X = var('X')
for k in range(1, e+1):
results = solve_mod([e*d0*X - k*X*(n-X+1) + k*n == X], 2^kbits)
for x in results:
p0 = ZZ(x[0])
p = partial_p(p0, kbits, n)
if p:
return p
if __name__ == '__main__':
n = 129796898134024157099156452709058687368221438176030502692200747714575571701027659861801365516981802018997712595009646737912670988500232545577601552315965176230630625733276337162755295073834150653688782811860047196091202071789102378530279205691266477048001888471022116120453815115157747843722970514365474705361
e = 7
d0 = 9519637250511849605092115946924531911819643854022344770386391196998091816870433223070160919249620469852108874736739746738237759468821919367674447147826813269165414967606625427817526475380034928092527497223
kbits = 343
p = find_p(d0, kbits, e, n)
print ("found p: %d" % p)
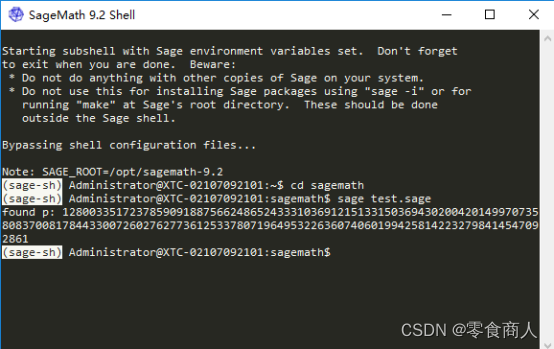
这样就成功分解了n,后续略。
Crypto-easybag
本题是标准的背包问题,由于结果模了一个p,所以先将pubkey的所有数模p处理。处理完成后将0-1背包转换为格结构,然后使用LLL算法求最短向量。由于我们不知道模p后的真实和是多少,所以通过爆破sum = c+i*p的i来确定。相应sage代码如下:
c = [...] # pubkey
sum = 300528310281431128814608316680537971945579270793936168485054801251195415271 # sum
def decrypt(enc,publickey):
# 维数
n = len(publickey)
# 构造格
d = 2*identity_matrix(ZZ,n,n)
col = publickey+[enc]
col = matrix(col).transpose()
last = matrix(ZZ,[[1]*n])
tmp = block_matrix(ZZ,[[d],[last]])
grid = block_matrix(ZZ,[[tmp,col]])
# 格基规约,使用LLL算法找到最短向量
M = grid.LLL()
# 利用最短向量还原信息
m = ''
for i in M[0]:
if i== -1:
m += '1'
elif i == 1:
m += '0'
return m
p = 94154607166206368507849450076562888867777996786776585204541315115554265673239
for i in range(33):
print(i)
m = decrypt(sum+i*p, c)
print(m)
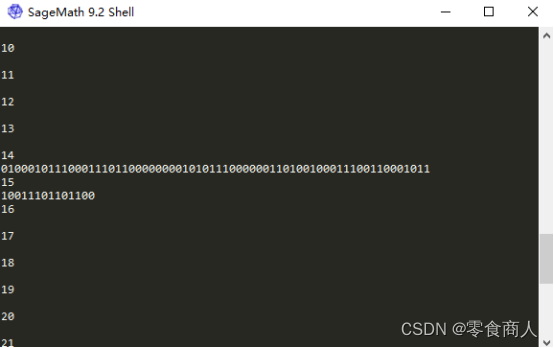
可以发现解出了m,转为字符串即为key,复写2遍即为秘钥,后续略
Misc-失窃的秘密
过滤MySQL流量,发现TCP流中有许多hex格式的文件:
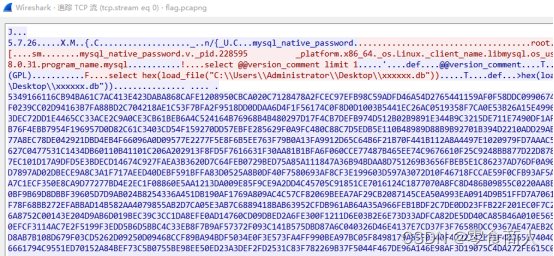
逐个取出后,总共获得4个文件:xxxxxx.db、key.txt、Login Data和Cryptography。其中Login Data是一个sqlite3数据库,查看信息如下:
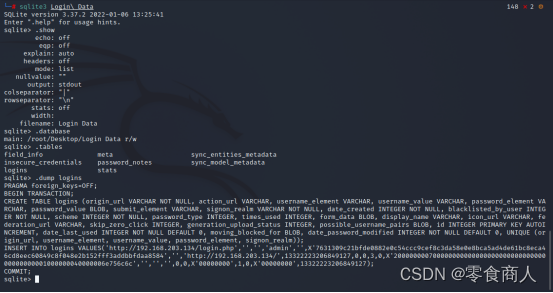
dump logins表后,得到admin用户密码的密文。根据文件名提示,Login Data是chrome浏览器保存password的文件名,所以此处大概率是chrome保存的密码内容,key.txt则为密钥。Chrome浏览器的密码加密方式为CryptProtectData,与标准AES-GCM略有不同,写代码解密如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Cryptodome.Cipher import AES
decrypted_key = "25ee84dbcdb3ed8882b6787771896f285edc1fbe49afe0a6934f8cecfe865139".decode('hex')
data = "7631309c21bfde0882e0c54ccc9cef8c3da58e0e8bca5ad4de61bc8eca46cd8eec60849c8f048e2b152fff3addbbfdaa8584".decode('hex')
nonce = data[3:3 + 12]
ciphertext = data[3 + 12:-16]
tag = data[-16:]
cipher = AES.new(decrypted_key, AES.MODE_GCM, nonce=nonce)
plaintext = cipher.decrypt_and_verify(ciphertext, tag)
print plaintext
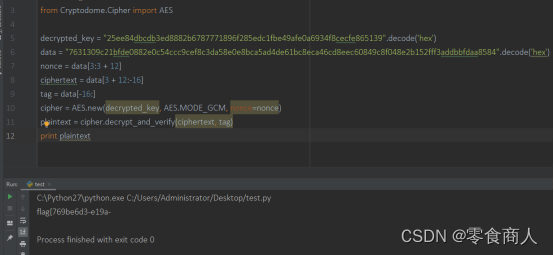
得到flag的前半部分。flag的另一半则需要剩下的两个文件。Cryptography可以用文本打开,里边内容类似注册表

根据表项内容,该文件来自HKEY_LOCAL_MACHINE\SOFTWARE\ Microsoft\Cryptography。跟这个表项相关的有很多游戏修改方式,将此处的MachineGuid复制到外部应用数据库中用以进行解密与信息提取。此处考察的是360浏览器的密码提取,提取对象就在最后一个文件xxxxxx.db中。使用专用提取工具带上MachineGuid进行提取,工具下载地址如下:
https://github.com/hayasec/360SafeBrowsergetpass
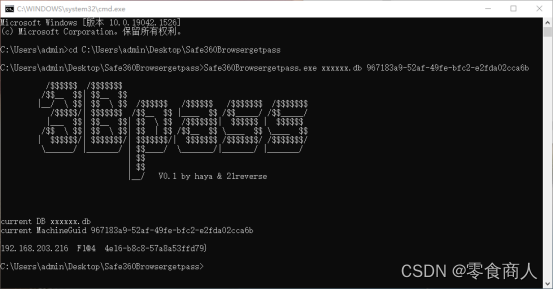
Misc-ezusb
本题打开后发现为键盘流量
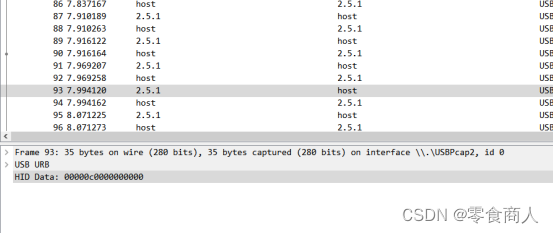
提出长度为35的数据包,数据的首位代表shift,第三位代表键盘代码,根据键盘流量对照表即可获得flag
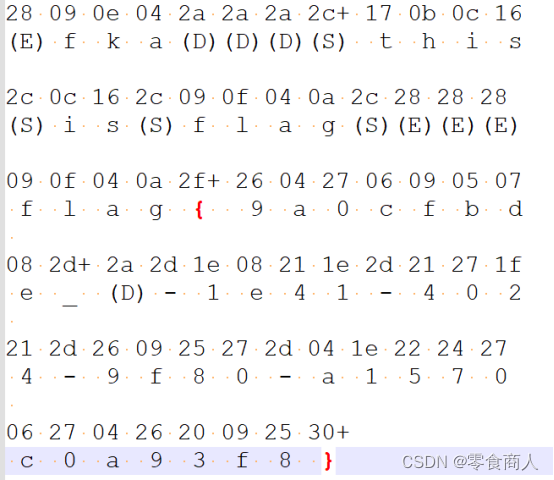
(D)=Delete,(E)=Enter,(S)=Space
Misc-AreYouOK Pro
题目给出的文件为pcap流量,改文件后缀后打开
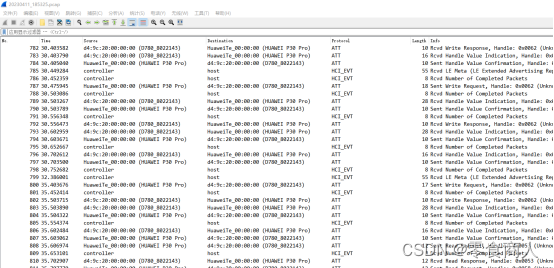
可以发现是一个设备与一台华为P30Pro手机通信的流量。在RFCOMM协议中发现文件传输信息。
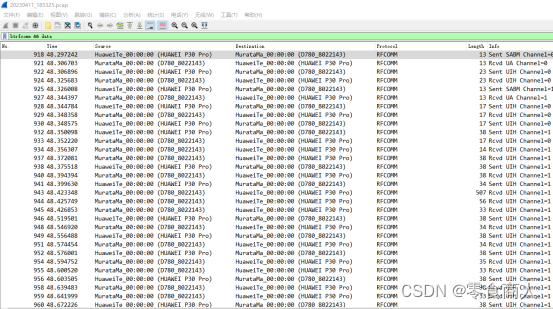
其中设备向手机传输内容较多,过滤目的地,可以发现从数据包968开始,设备向手机传输了一个巨大的文件。
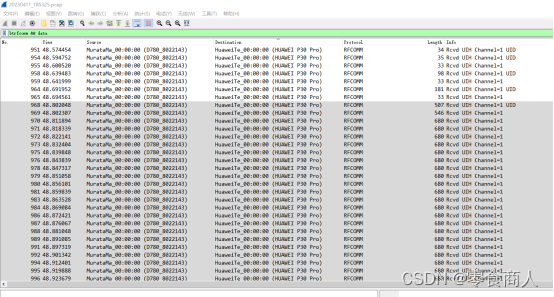
将这些数据包导出为json,提取其中data段信息并扔掉报文头后,发现内容为一张图片,保存出来。
#!/usr/bin/env python
# -*- coding: utf-8 -*-
import json
packets = json.loads(open("1.json", "r").read())
data = ""
for packet in packets:
data += packet["_source"]["layers"]["data"]["data.data"].replace(":", "")
data = data.split("a5a50100")
newdata = ""
for x in data:
newdata += x[8:]
open("111.png", "wb").write(newdata[24:].decode('hex'))
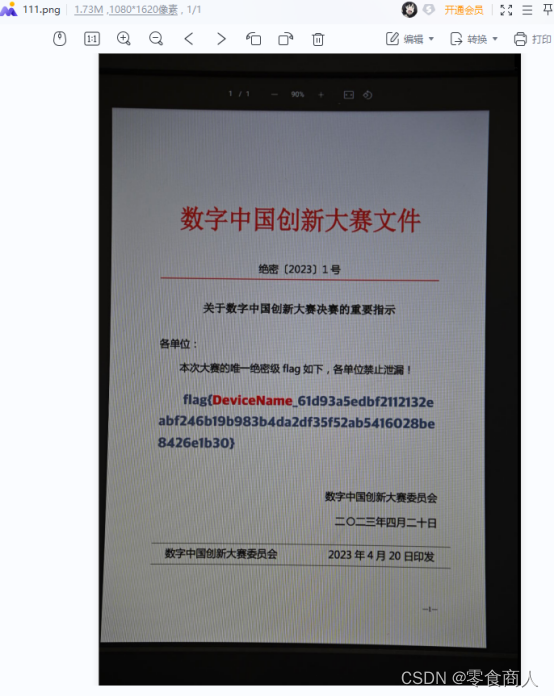
其中DeviceName在数据包中直接可以读出,为D780_8022143
Reverse-crackme
这题其实可以不用看题目中的加密算法,我们可以化简题目的加密过程如下:
假设加密函数是f(x),注册用户名是user_id,注册机器码是machine_id,注册号是key。
题目判断条件是f(key) == f(f(f(machine_id)[:16]+f(user_id)[:16]))
可得当key = f(f(machine_id)[:16]+f(user_id)[:16])
通过patch程序可以将程序内写死的机器码改为题目给的1653643685031597,然后在下图位置下断点。
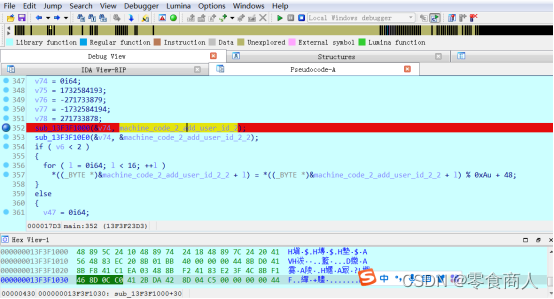
运行程序,输入user_id=xiaoming,即可获得f(f(machine_id)[:16]+f(user_id)[:16])。
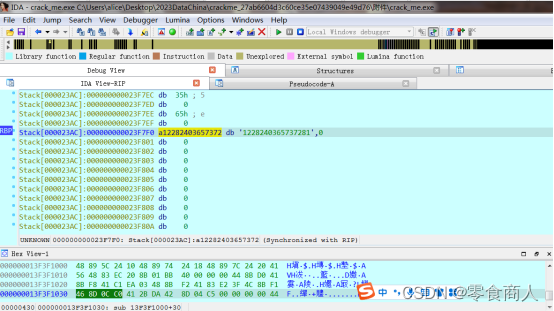
Misc-Encryptedfile
打开程序,发现是个加密用的程序,密码为4为数字
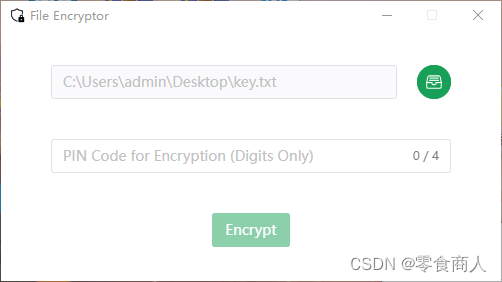
随便选择一个文件加密,提示File encrypted
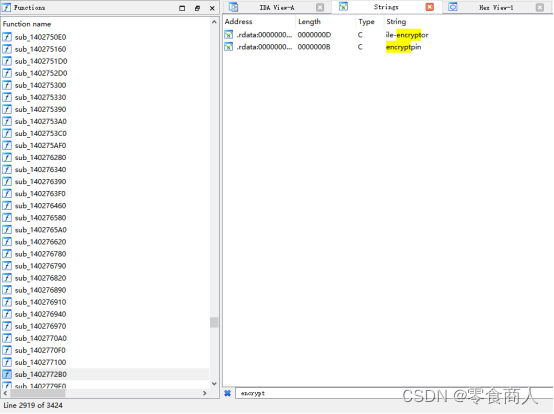
扔进IDA搜索关键字,发现两个字符串和encrypt相关。其中第一个字符串没有引用,第二个有
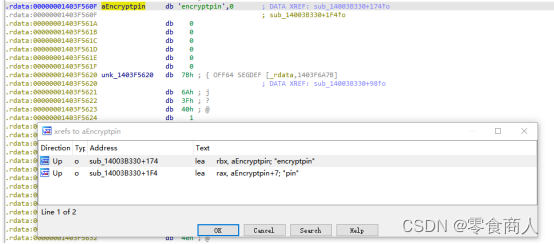
跳转后发现堆栈不平衡,需要修复。将所有内容部分纳入编译(C键),可以看到正确工作流程的函数。

从此处向下看,sub_140073A70疑似为读取数据;sub_140039890函数同样堆栈不平衡,需要修复,修复后内容非常多,应该是加密的核心函数。
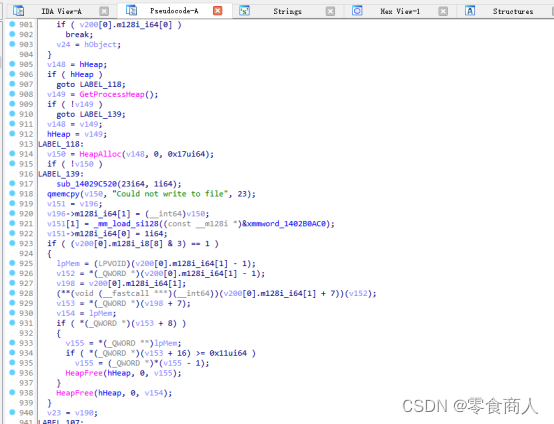
在该函数中,找到大量对7、9、13位进行操作的循环代码

此类加密变换类似Salsa20的加密变换,但Salsa20加密依然需要两个元素:一是32为字符构成的key,二是随机生成的8为nonce。算法使用key和nonce生成一个2^70长度的序列,并与明文进行异或加密。在上方可以看到如下内容:
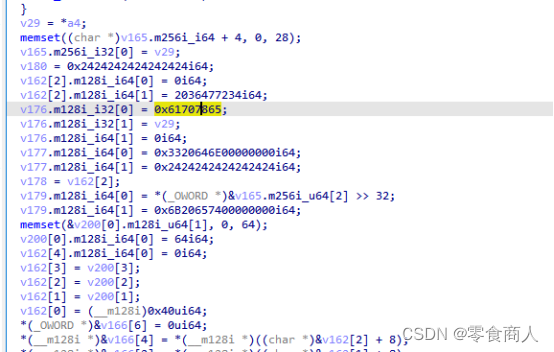
其中0x61707865、0x3320646E均为Salsa20算法的固定参数,所以确认本题为Salsa20算法。

在上述参数中同样有key和nonce,其中key为v29所在位置,nonce在0x3320646E后,为八个0x24。
接下来看key的来源。key=v29来自输入a4,可能和输入相关。启动动态调试,在此处设置断点进行观察:
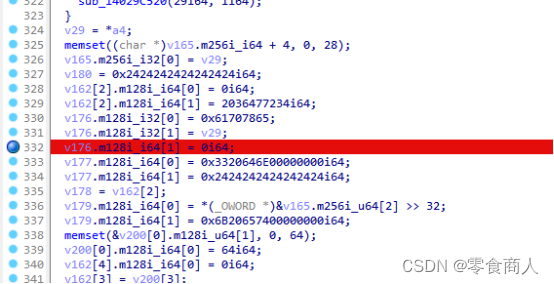
输入秘钥1234,随便加密一个文件,程序在断点处停止运行,可以看到v29即当前EAX的值为0x34333231,即我们输入的1234明文
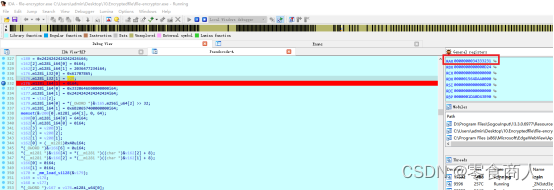
因此猜测此处的key未进行任何变化,直接填充到了32字符。
接下来处理密文。由于密码只有0000~9999这10000种可能,加密后文件名又是flag.png.enc,所以原文件是个png文件,使用png固有文件头89504E47来判断解密是否成功,写出解题代码如下:
#!/usr/bin/env python
# -*- coding: utf-8 -*-
from Cryptodome.Cipher import Salsa20
cipher = open("flag.png.enc", "rb").read()
for i in range(10000):
key = str(i).rjust(4, '0').ljust(32, '\x00')
nonce = '\x24\x24\x24\x24\x24\x24\x24\x24'
sal = Salsa20.new(key=key, nonce=nonce)
plain = sal.decrypt(cipher)
if plain.find("\x89\x50\x4E\x47")>=0:
open("flag.png", "wb").write(plain)
break