文章目录
- 整数拆分
- 题解(动态规划)
- 贪心
- 不同的二叉搜索树
- 题解
整数拆分
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (62.22%) | 1166 | 0 | - | - | 0 |
数学 | 动态规划
给定一个正整数 n ,将其拆分为 k 个 正整数 的和( k >= 2 ),并使这些整数的乘积最大化。
返回 你可以获得的最大乘积 。
示例 1:
输入: n = 2
输出: 1
解释: 2 = 1 + 1, 1 × 1 = 1。
示例 2:
输入: n = 10
输出: 36
解释: 10 = 3 + 3 + 4, 3 × 3 × 4 = 36。
提示:
2 <= n <= 58
Discussion | Solution
题解(动态规划)
// @lc code=start
class Solution {
public:
int integerBreak(int n) {
vector<int> dp(n+1);
dp[2] = 1;
for(int i = 3; i <= n; ++i) {
for(int j = 1; j <= i/2; ++j) {
dp[i] = max(dp[i],max((i-j) * j,dp[i-j]*j));
}
}
return dp[n];
}
};
- 时间复杂度:O(n^2)
- 空间复杂度:O(n)
贪心
本题也可以用贪心,每次拆成n个3,如果剩下是4,则保留4,然后相乘,但是这个结论需要数学证明其合理性!
我没有证明,而是直接用了结论。感兴趣的同学可以自己再去研究研究数学证明哈。
给出我的C++代码如下:
class Solution {
public:
int integerBreak(int n) {
if (n == 2) return 1;
if (n == 3) return 2;
if (n == 4) return 4;
int result = 1;
while (n > 4) {
result *= 3;
n -= 3;
}
result *= n;
return result;
}
};
- 时间复杂度:O(n)
- 空间复杂度:O(1)
不同的二叉搜索树
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (70.86%) | 2213 | 0 | - | - | 0 |
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
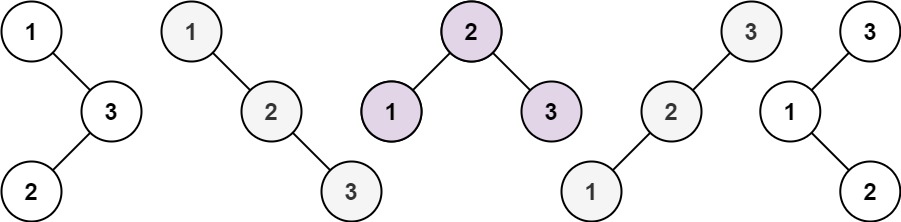
输入:n = 3
输出:5
示例 2:
输入:n = 1
输出:1
提示:
1 <= n <= 19
Discussion | Solution
题解
// @lc code=start
class Solution {
public:
int numTrees(int n) {
vector<int> dp(n+1);
dp[0] = 1;
for(int i = 1;i <=n; ++i) {
for(int j = 1; j <= i;++j) {
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
};
for(int j = 1; j <= i;++j) {
dp[i] += dp[j-1] * dp[i-j];
}
}
return dp[n];
}
};
参考文章:[代码随想录 (programmercarl.com)](https://programmercarl.com/0096.不同的二叉搜索树.html#思路)