占据栅格地图（Occupancy Grid Map）

占用栅格地图基础概念

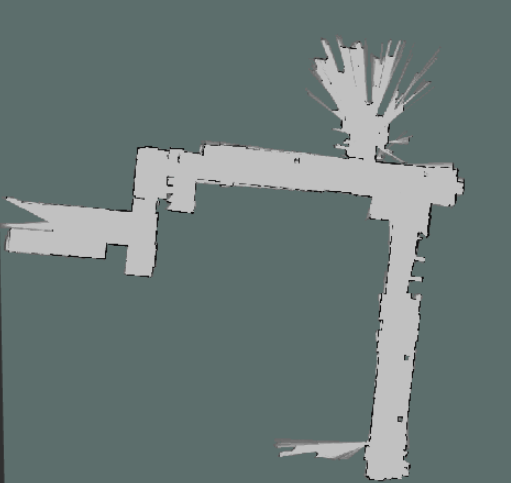
上图就是一个ROS中的占据栅格地图显示

栅格地图定义 ：栅格地图就是用一个个栅格组成的网格来代表地图. 栅格里可以存储不同的数值, 代表这个栅格的不同含义.

ROS的栅格地图使用

• 白色代表空闲，也就是可通过区域，其存储的值为 0；
• 黑色代表占用，也就是不可通过区域，其存储的值为 100；
• 灰色代表未知，就是说目前还不清楚这个栅格是否可以通过，其存储的值为 -1．

占据栅格地图的数学模型

占据率（Occupancy）
在通常的尺度地图中，对于一个点，它要么有（Occupied状态）障碍物，要么没有（Free状态）障碍物
在占据栅格地图中，对于一个点，用$$p(s=0)$$来表示它是Free状态的概率;

用$$p(s=1)$$来表示它是Occupied状态的概率.两者的和为1

引入两者的比值来作为点的状态：$$Odd(s)=\frac{p(s=1)}{p(s=0)}$$

对于一个点，新来了一个测量值,之后我们需要更新它的状态,假设测量值来之前，该点的状态为$$Odd(s)$$，
我们要更新它为：$$Odd(s|z)=\frac{p(s=1|z)}{p(s=0|z)}$$
这种表达方式类似于条件概率，表示在发生z的条件下s的状态。

根据贝叶斯公式，我们有：
$$p(s=1|z)=\frac{p(z|s=1)p(s=1)}{p(z)}$$
$$p(s=0|z)=\frac{p(z|s=0)p(s=0)}{p(z)}$$

带入$Odd(s|z)$中得到
$$Odd(s|z)=\frac{p(s=1|z)}{p(s=0|z)}=\frac{p(z|s=1)p(s=1)/p(z)}{p(z|s=0)p(s=0)/p(z)}=\frac{p(z|s=1)}{p(z|s=0)}Odd(s)$$

对两边取对数得：

$$logOdd(s|z)=log\frac{p(z|s=1)}{p(z|s=0)}+logOdd(s)$$

这样，含有测量值的项就只剩下了$$log\frac{p(z|s=1)}{p(z|s=0)}$$称这个比值为测量值的模型,标记为$$lomeas$$
测量值的模型只有两种$$lofree=log\frac{p(z=0|s=1)}{p(z=0|s=0)}$$和$$looccu=log\frac{p(z=1|s=1)}{p(z=1|s=0)}$$

这样，如果我们用$Odd(s)$来表示位置s的状态S的话，我们的更新规则就进一步简化成了：$$S^{+}=S^{-}+lomeas$$
其中$$S^{+}$$和$$S^{-}$$分别表示测量值之后和之前的状态。

另外，在没有任何测量值的初始状态下，一个点的初始状态$$S_{init}=logOdd(s)=log\frac{p(s=1)}{p(s=0)}=log\frac{0.5}{0.5}=0$$

经过这样的建模，更新一个点的状态就只需要做简单的加减法了。

例如
假设我们设定$$looccu=0.9$$ $$lofree=-0.7$$
那么， 一个点状态的数值越大，就表示越肯定它是Occupied状态，相反数值越小，就表示越肯定它是Free状态。

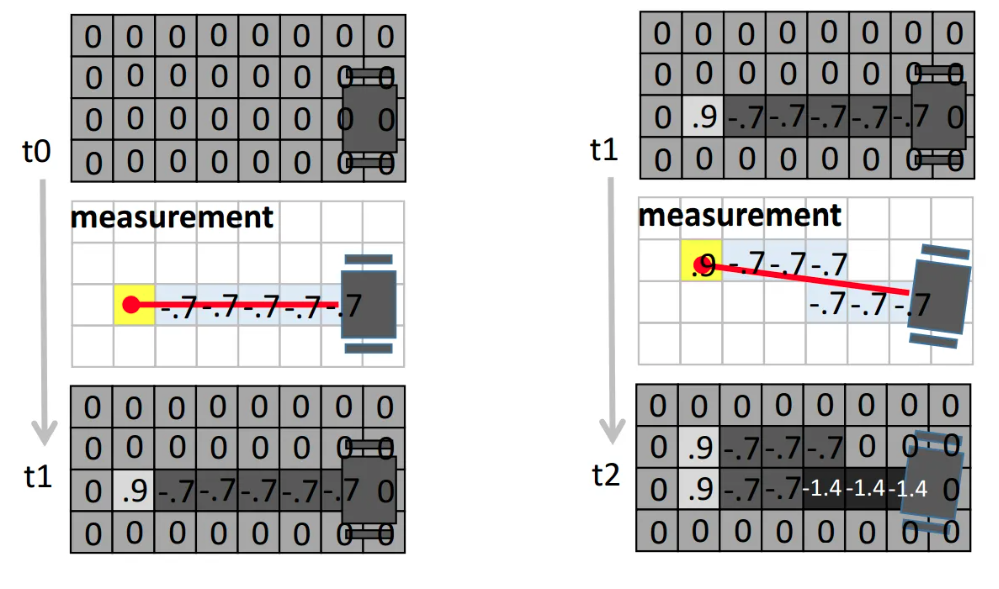
上图就展示了用两个激光传感器的数据更新地图的过程。在结果中，一个点颜色越深表示越肯定它是Free的，颜色越浅表示越肯定它是Occupied的。

ROS中使用OccupancyGrid

在ros中的数据格式定义如下：（官网链接）

std_msgs/Header header
nav_msgs/MapMetaData info
int8[] data

后续
详情参考 古月居