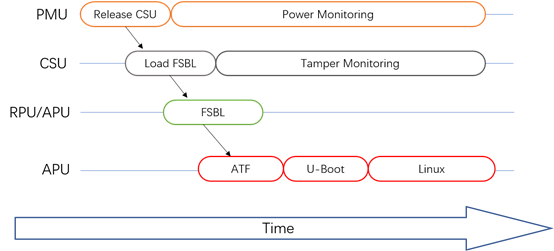
线性结构的存储类型
顺序标:顺序标就是数组,也成为向量vector、高维向量及称为张量即tensor
链表:单链表、双链表、循环链表
线性表概念
表目、文件、索引、表的长度、空表
线性表由节点表和关系表组成二元组;
- 节点集由有限的顺序元素组成,关系则有前驱、后继关系。第一个元素称为表头,最后一个元素称为表尾,其他都是内部元素。前驱后继关系具有反对称性和传递性。
- 元素在线性表中的位置称为下标或者是索引。
- 元素的个数称为表长,长度为0的表就是空表,线性表易于存储和操作。
线性表按照访问方式分为三种类型:
- 直接访问型:可以根据下标定位元素的位置。如数组向量就是直接访问的线性表,单个的记录类型也是线性结构
- 目录索引型:例如字典还有散列表
- 顺序访问型:必须在表中挨个查找所需元素,例如链表,为了提高检索的速度,做一些有效的索引。
数据结构由逻辑、存储和运算三个因素的不同,只要有一个有所不同,就可以看作不同的数据结构。
线性表的逻辑结构
- 线性表的长度
- 表头
- 表尾
- 当前位置

线性表的存储结构:
顺序表:按照索引值从小到大存在一片相邻的连续区域
紧凑结构

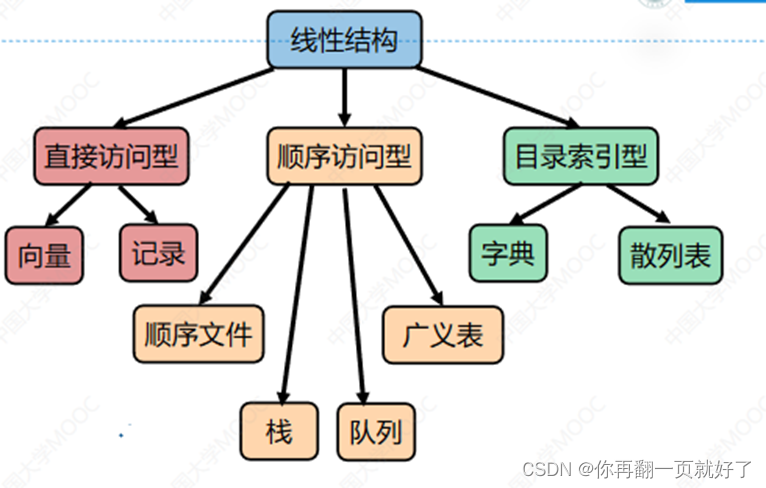
链表: - 单链表
- 双链表
- 循环链表
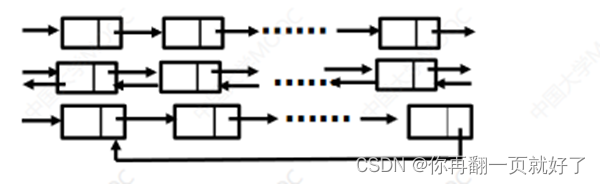
根据存储结构不同分为数组、链表
顺序表是一个非常高效的存储结构就表达了逻辑关联,不需要额外的存储域就表达逻辑上相邻关系
链表需要通过指针的关系来表达逻辑顺序,因此需要指针这样的额外存储空间
另外,链表的存储效率不如顺序表
线性表分类:
线性表
–不限制操作
栈
–插入和删除都在同一端进行
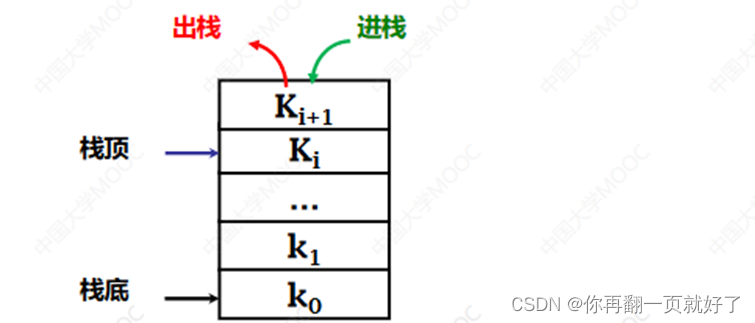
按照操作可以把线性表分为普通线性表、栈、队列三种
普通的线性表,操作不受任何限制
栈的插入和删除在同一端进行
队列的插入和删除分别在两端进行
栈的先进后出的性质,在深度优先搜索、递归等算法中有很好地应用
队列的先进先出的性质,在宽度优先搜索、层次化处理算法中有很好的应用
顺序表
定义:
顺序表节点的定义基本上继承了线性表的模板,不同的是首先要定义一个数组,数组的最大长度为maxsize,数组当前元素的个数为curlen,只有在下标零到当前元素的区间中的那些数据在逻辑上是有效的
顺序表的操作:
跟线性表ADT中定义已知,主要是增删查改,定义了线性表的类模板接口以后,顺序或链式的不同实现方式,其相应的运算函数接口是一致的,因此在构造上一层应用的时候,调用的方式不需要改变,只要修改相应的头文件就可以。
顺序表中插入元素的方法
1;append是在表尾添加元素
2;insert在当前位置之前插入元素
顺序表的插入和删除操作
顺序表的插入操作还是需要保证逻辑结构和存储结构一致,是当前的待插入位置,首先要腾空,我们把相应的数据元素逐个下移,最后把待插入的元素X填入腾空的位置

顺序表插入的算法:
1;传入的参数是当前位置p和待插入的值value,判断一下表中是否还有存储空间;
2;如果表已经满了,则插入失败;
3;否则擦好看待插入位置p是否在表的逻辑长度范围内也就是[0, curlen]之间,如果越界,则不允许插入;
4;如果是一个有效的可插入位置,从表尾开始到待插入的位置的元素,逐个后移一位,接着把待插入的元素填入刚腾出的位置P,完成插入操作,线性表规模增加了1,返回值表示插入成功。
5;删除是插入的逆操作,为了保持逻辑和存储对应,删除当前元素知乎,从下一个元素已知到表尾逐个往上移,当前线性表的元素个数-1
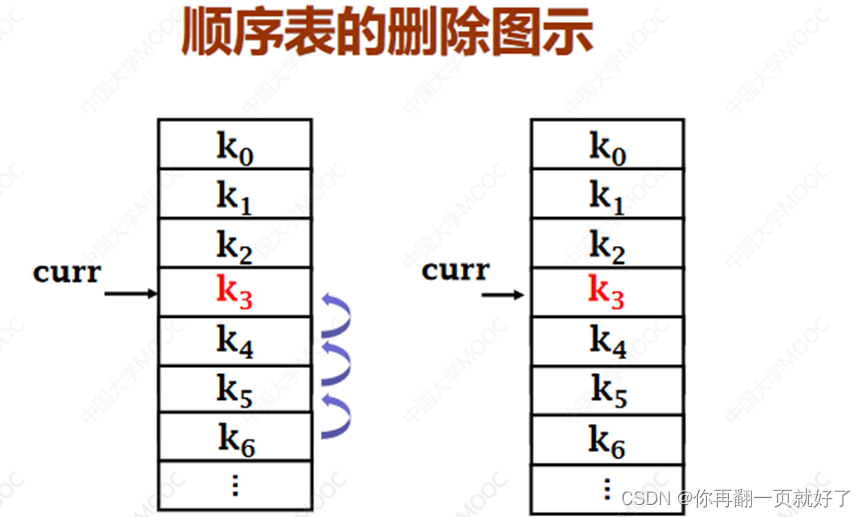
顺序表的删除算法
1;首先传入待删除的下标位置p,检查当前的长度,如果小于等于零,那就是空表,不允许删除。
2;检查下标P是不是在[0,curlen],合理的顺序表元素范围之内,如果超出当前表的下标范围,则报告删除操作非法;
3;对于合法的下标范围的p,从当前元素一直到表尾,把后面的元素逐个往前移,表的实际长度缩短1;
4;删除后顺序表还保持了紧密的存储特性,也就是存储结构保留了顺序的逻辑顺序关系