这个专栏名为《Numpy从入门到精通》,顾名思义,是记录自己学习numpy的学习过程,也方便自己之后复盘!为深度学习的进一步学习奠定基础!希望能给大家带来帮助,爱睡觉的咋祝您生活愉快! 这一篇介绍《Numpy从入门到精通——广播机制》
文章目录
- 一、np与math库比较
- 二、与单一元素进行运算
- 三、循环与向量运算比较
一、np与math库比较
使用过python的同学相信对math都不陌生,在我很早的博客中也提及到math库的使用,具体可以看链接链接: 八种方法求π的近似值,
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project :numpy学习
@File :task_11.py
@IDE :PyCharm
@Author :咋
@Date :2023/4/17 22:09
"""
import time
import math
import numpy as np
x = [i * 0.001 for i in np.arange(1000000)]
start = time.time()
for i, t in enumerate(x):
x[i] = math.sin(t)
print("math.sin:", time.time() - start)
x = [i * 0.001 for i in np.arange(1000000)]
x = np.array(x)
start = time.time()
np.sin(x)
print("numpy.sin:", time.time() - start)
输出:
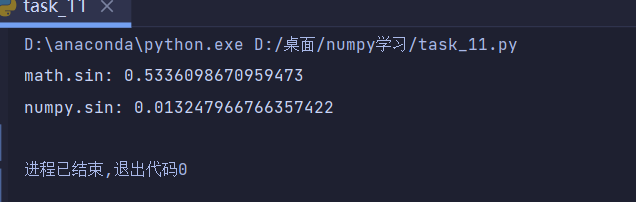
可以看到np的速度是math的进50倍。
下面再看一个例子:
def basic_sigmoid(x):定义basich_sigmoid函数,需要一个参数x
"""
Compute sigmoid of x.
Arguments:
x -- A scalar
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1.0 / (1.0 + 1.0 / math.exp(x)) math.exp(x) 相当于自然系数e的x次方
上一行写成公式就是s=1/(1+e^x )
### END CODE HERE ###
return s返回s
basic_sigmoid(3) 调用上面定义的函数
x = np.linspace(-5,5,1000) 从-5到5生成1000个数
y = [] 定义一个列表
for i in range(1000): 循环
y.append(basic_sigmoid(x[i])) 调用上面的函数,传入一个数字,即可通过函数生成一个值,将生成值添加到列表上
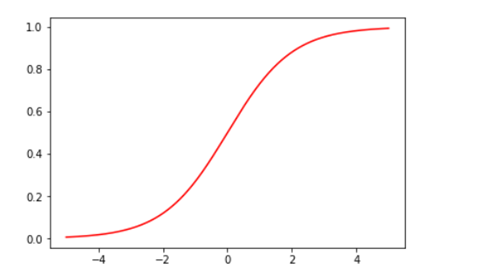
plt.plot(x,y,c="r") 通过一系列(x,y),用plt将图画出来,
画出来的图如图一:
### One reason why we use "numpy" instead of "math" in Deep Learning ###
x = [1, 2, 3]
basic_sigmoid(x) # you will see this give an error when you run it, because x is a vector.传入的是列表会报错,之前定义的函数需要出人的是具体的数值,所以传入一个列表会报错
import numpy as np 导入numpy模块
# example of np.exp
x = np.array([1, 2, 3]) 创建一个numpy矩阵,值为1,2,3
print(np.exp(x)) # result is (exp(1), exp(2), exp(3)) 将numpy矩阵传入进去,发现可以正常运行,结果为[ 2.71828183 7.3890561 20.08553692]
# example of vector operation
x = np.array([1, 2, 3])
print (x + 3) numpy矩阵整体+1,结果为np.array([4 5 6])
# GRADED FUNCTION: sigmoid
import numpy as np # this means you can access numpy functions by writing np.function() instead of numpy.function() 给numpy取了个别名np,减少了代码量
def sigmoid(x):
"""
Compute the sigmoid of x
Arguments:
x -- A scalar or numpy array of any size
Return:
s -- sigmoid(x)
"""
### START CODE HERE ### (≈ 1 line of code)
s = 1.0 / (1.0 + np.exp(-1.0 * x)) 和上面相同,np.exp也是e的x次方,写成公式为:
s=1/(1+e^(-x) )
### END CODE HERE ###
return s返回s的值
x = np.array([1, 2, 3]) 创建numpy矩阵
sigmoid(x) 直接调用定义好的函数,不再需要for循环
x = np.linspace(-15,15,1000) 同上,创建-15到15的1000个数值
y = sigmoid(x) 将返回结果给y
plt.plot(x,y,c="r") plt绘图
plt.show() 展示图片
图片如下:
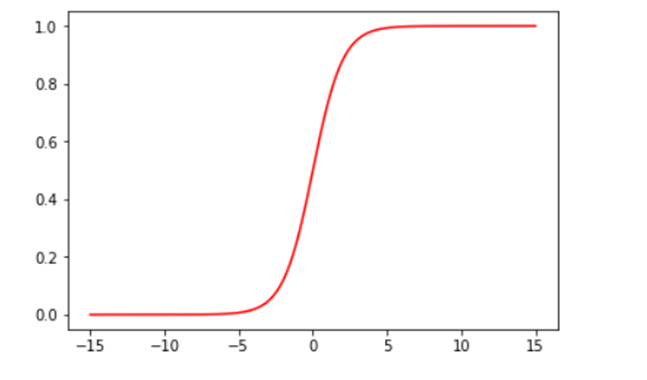
总结:通过这个小案例,我们知道了numpy矩阵可以直接运算,这正是深度学习使用numpy库而非math库的原因,在深度学习中,有大量矩阵的相关运算,使用numpy可以提升运算的速度并减少代码量,numpy是一个很好用的科学计算库!
二、与单一元素进行运算
利用numpy的广播机制,可以将np矩阵与单一元素直接进行运算,我们直接看代码示例:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project :numpy学习
@File :task_12.py
@IDE :PyCharm
@Author :咋
@Date :2023/4/17 22:23
"""
import numpy as np
A = np.array([[1, 2], [-1, 4]])
print("+运算:")
print(A+1)
print("-运算:")
print(A-1)
print("*运算:")
print(A*2)
print("除整数运算:")
print(A/2)
print("除小数运算:")
print(A/2.0)
输出:
+运算:
[[2 3]
[0 5]]
-运算:
[[ 0 1]
[-2 3]]
*运算:
[[ 2 4]
[-2 8]]
除整数运算:
[[ 0.5 1. ]
[-0.5 2. ]]
除小数运算:
[[ 0.5 1. ]
[-0.5 2. ]]
三、循环与向量运算比较
由于numpy具有广播机制的特性,使得ndarray能够不借助for循环直接运行,速度大大提升,但值得注意的是numpy不支持GPU运算:
#!/usr/bin/env python
# -*- coding: UTF-8 -*-
"""
@Project :numpy学习
@File :task_13.py
@IDE :PyCharm
@Author :咋
@Date :2023/4/17 22:32
"""
import time
import numpy as np
x1 = np.random.rand(1000000)
x2 = np.random.rand(1000000)
##使用循环计算向量点积
tic = time.process_time()
dot = 0
for i in range(len(x1)):
dot += x1[i] * x2[i]
toc = time.process_time()
print("dot = " + str(dot) + "\n for loop----- Computation time = " + str(1000 * (toc - tic)) + "ms")
##使用numpy函数求点积
tic = time.process_time()
dot = 0
dot = np.dot(x1, x2)
toc = time.process_time()
print("dot = " + str(dot) + "\n verctor version---- Computation time = " + str(1000 * (toc - tic)) + "ms")
输出:
dot = 249929.02170318714
for loop----- Computation time = 187.5ms
dot = 249929.0217031858
verctor version---- Computation time = 15.625ms
for循环的时间是向量运算的400倍,这也再次证明了深度学习算法中一般都用向量化的矩阵运算!