主要学习的是这篇文章,但大佬并没有在文章里面仔细的讲g2o,所以我在网上找了这几篇介绍g2o的文章,讲的十分详细,对入门十分友好:文章一、文章二、文章三,这三篇都是一个作者写的,主要是针对编程实际操作。
g2o入门
一、图优化是什么?
区分两个不同的概念:
1)图优化(graph-base optimization)
2)凸优化(convex optimization)
很多时候容易搞混淆,我第一次听到图优化这个词的时候,看到实验室有一本书名叫《凸优化》还以为是这个,但两个是完全不同的概念,在这里进行区分。图优化的图是数据结构里面的图,凸优化里面的凸是凸函数。
slam后端一般有两种方法,第一个是EKF(扩展卡尔曼滤波器)为代表的滤波方法;第二个就是以图优化为代表的非线性方法。当前slam研究热点几乎都是基于图优化的。
图优化里的图就是i数据结构里面的图,一个图有若干个定点(vertex),以及连接这些顶点的边(edge)。举例:一个机器人在房间中移动,它在某个时刻t的位姿(pose)就是一个顶点,这个就是一个待优化变量。而位姿之间的关系就构成一个边,比如t时刻和t+1时刻之间的相对位姿变换矩阵T就是边,边通常表示误差项。
在slam中,图优化一般分解为两步:
第一步:构建图。将机器人的位姿作为顶点,位姿间的关系作为边。
第二步:优化图。调整机器人的位姿(顶点)来尽量满足边的约束,使得误差减少。
举例:
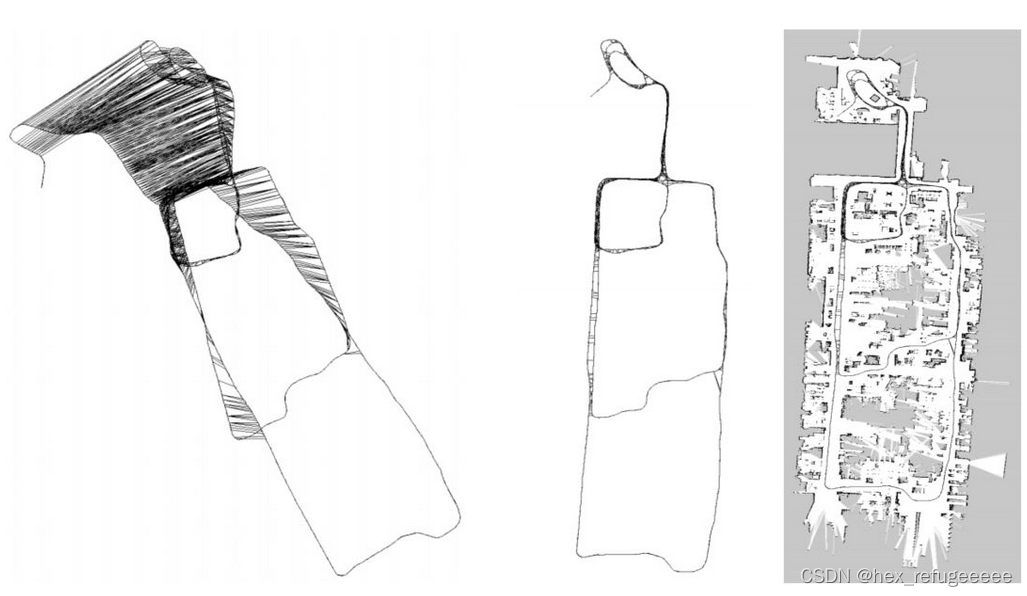
在机器人运行过程中,将机器人不同时刻t的位姿pose作为顶点(vertex),这个位姿可能来源与机器人自身携带的编码器或者是icp、ndt配准算法求得。图的边就是位姿之间的关系。但在机器人运行的过程中,会出现很多的误差,如图左,然后通过图优化,设置边的约束关系,就可以获得图中,与图右之间的差别就很小了。但我现在不太知道这个图左的轨迹是什么?一个是真值另一个是计算出来的轨迹吗?
二、g2o框架
在slam后端图优化一般有g2o、gtsam和ceres,这里主要介绍g2o,以后应该还会学习gtsam。
g2o全称:General Graph Optimization,是一个用来优化非线性误差函数的c++框架。简单来说就是它把优化的框架搭建好了,使用者只用专注与输入的顶点和边的建立,然后使用它优化的结果。将slam后端优化在工程实现上变的更加简单。
g2o官网:GitHub - RainerKuemmerle/g2o: g2o: A General Framework for Graph Optimization
文献:
《g2o: A General Framework for Graph Optimization》
《A Tutorial on Graph-Based SLAM》
文献以后有机会在看,先会用再说。
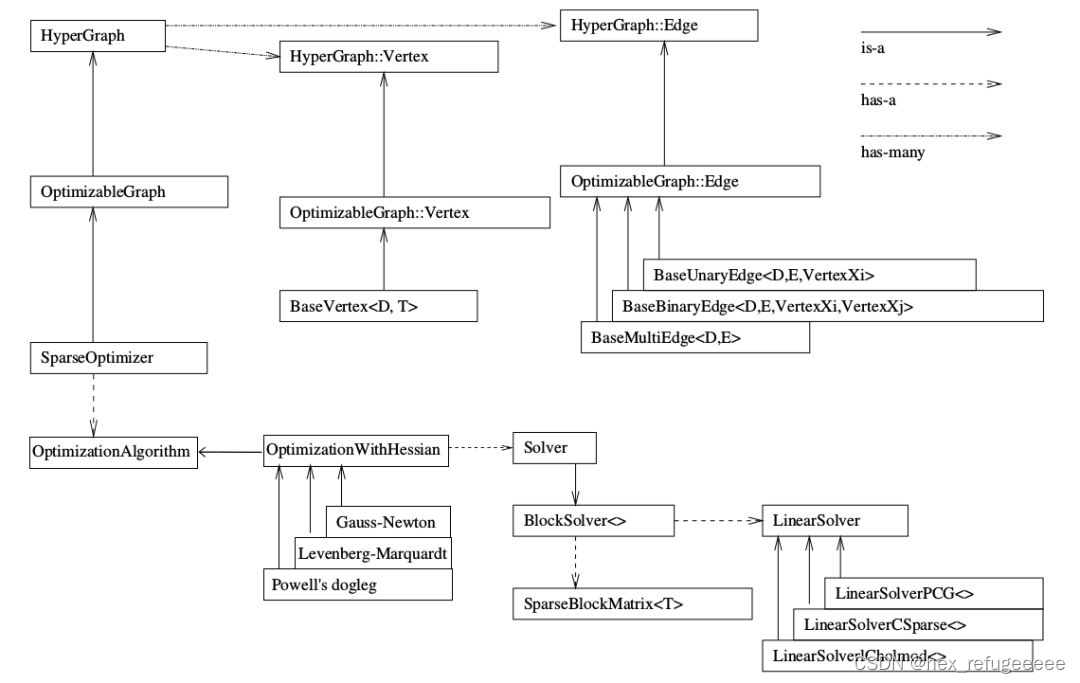
这是官网上关于g2o整个框架的介绍,简单明确
首先看向图片的右上角,关于"is a"、"has a"、"has many"这三个箭头的含义。最初看这个图的时候,这三个的意思一直不得要领,怎么理解都很别扭。后来感觉是不是和c++中的继承关系有关,直接按照c++ is a在搜索引擎里面寻找,果然就是我想的这样。这里来简单解释一下,方便之后的理解。
水果Fruit、香蕉Banana、午餐Lunch、米饭Rice
Banana is a kind of Fruit.
上面说的是香蕉是一种水果,is a,将它们抽象到c++的class中的继承关系就是这样的:
class Banana : public Fruit,就是Banana继承自Fruit。
这就是is a的简单理解。
Lunch has a Fruit.(可能语法有问题,不要在意)
说的是午餐有水果,也可能有别的米饭Rice什么的。它们就是一种包含关系,在class中就是这样的。
class Lunch
{
class Fruit{};
class Rice{};
...
}
大概就是这个道理,就是表示一种class间的继承关系。
现在来分析这张图:
首先看最左边的SparseOptimizer(稀疏优化器),按向上的箭头阅读,就是说SparseOptimizer is a OptimizableGraph,说SparseOptimizer是一个OptimizableGraph(可优化的图)。而OptimizableGraph is a HyperGraph(超图)。
重点就是这个HyperGraph它连接的是has many的箭头,这些箭头指向了图优化中的顶点(HyperGraph::Vertex)和边(HyperGraph::edge),就是前面午饭和水果、米饭的关系。
在HyperGraph::Vertex(顶点)可以看到OptimizableGraph::Vertex指向了它,说明OptimizableGraph::Vertex is a HyperGraph::Vertex。OptimizableGraph::Vertex继承自HyperGraph::Vertex,类似的可以推出BaseVertex<D,T>继承自OptimizableGraph::Vertex。具体请看后面对g2o的源码分析。这里的继承自也可以理解为通过xx来实现。
再通过SparseOptimizer往下看,SparseOptimizer has a OptimizationAlgorithm(优化算法)。然后这个OptimizationWithHessian is a OptimizationAlgorithm。就是说OptimizationAlgorithm 是通过OptimizationWithHessian来实现的。然后OptimizationWithHessian有三个迭代的方法:Gauss-Newton(高斯牛顿法,简称GN), Levernberg-Marquardt(简称LM法), Powell's dogleg。之后就是对于OptimizationWithHessian类的的内容进行分析,OptimizationWithHessian has a Solver,OptimizationWithHessian类里面有一个Solver(求解器)。然后对这个Solver进行分析。Solver is a BlockSolver。BlockSolver包含了两个类SparseBlockMatrix<T>用于计算稀疏的雅可比和Hessian矩阵和LinearSolver它用于计算迭代过程中最关键的一步HΔx=−b。LinearSolveru有三个PCG, CSparse, Choldmod方法。
三、g2o运行流程
在前面的框架图中,介绍是从上到下的。在g2o的运行过程中是从下到上的。
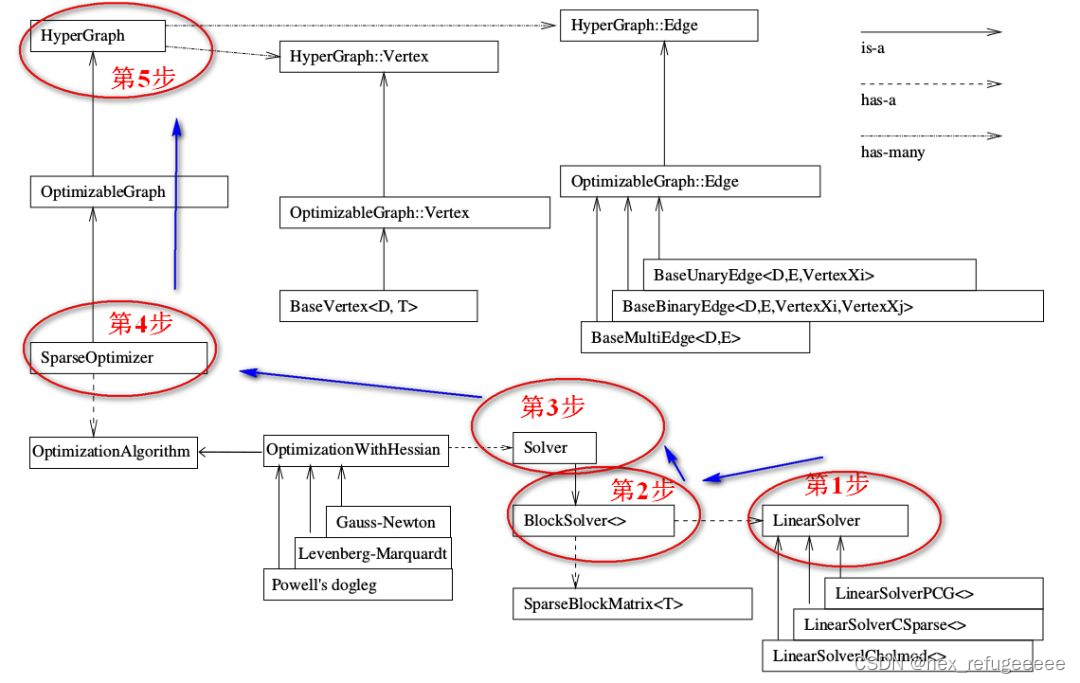
整个流程是这样的:
第一步:先确定采用什么线性求解器。
第二步:使用第一步的线性求解器初始化BlockSlover<>。
第三步:从三个迭代方法中选择合适的并使用第二步获得的BlockSlover<>来初始化Solver。
第四步:创建核心SparseOptimizer.
第五步:定义顶点和边,然后添加到SparseOptimizer中去。
根据高博十四讲里面介绍使用g2o的源码分析:
// 构建图优化,先设定g2o
typedef g2o::BlockSolver<g2o::BlockSolverTraits<3, 1>> BlockSolverType; // 每个误差项优化变量维度为3,误差值维度为1
typedef g2o::LinearSolverDense<BlockSolverType::PoseMatrixType> LinearSolverType; // 线性求解器类型
//这里将前三步合并到一起了
// 梯度下降方法,可以从GN, LM, DogLeg 中选
auto solver = new g2o::OptimizationAlgorithmGaussNewton(
g2o::make_unique<BlockSolverType>(g2o::make_unique<LinearSolverType>()));
// 第四步
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出
// 第五步
// 往图中增加顶点
CurveFittingVertex *v = new CurveFittingVertex();
v->setEstimate(Eigen::Vector3d(ae, be, ce));
v->setId(0);
optimizer.addVertex(v);
// 往图中增加边
for (int i = 0; i < N; i++) {
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge(edge);
}高博这一版的源码前三步有点难理解,其实就是将第一步和第二步使用智能指针和第三步放在一行了,在文章一中有更加清晰的流程:
typedef g2o::BlockSolver< g2o::BlockSolverTraits<3,1> > Block; // 每个误差项优化变量维度为3,误差值维度为1 // 第1步:创建一个线性求解器LinearSolver Block::LinearSolverType* linearSolver = new g2o::LinearSolverDense<Block::PoseMatrixType>(); // 第2步:创建BlockSolver。并用上面定义的线性求解器初始化 Block* solver_ptr = new Block( linearSolver ); // 第3步:创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用上述块求解器BlockSolver初始化 g2o::OptimizationAlgorithmLevenberg* solver = new g2o::OptimizationAlgorithmLevenberg( solver_ptr ); // 第4步:创建终极大boss 稀疏优化器(SparseOptimizer) g2o::SparseOptimizer optimizer; // 图模型 optimizer.setAlgorithm( solver ); // 设置求解器 optimizer.setVerbose( true ); // 打开调试输出 // 第5步:定义图的顶点和边。并添加到SparseOptimizer中 CurveFittingVertex* v = new CurveFittingVertex(); //往图中增加顶点 v->setEstimate( Eigen::Vector3d(0,0,0) ); v->setId(0); optimizer.addVertex( v ); for ( int i=0; i<N; i++ ) // 往图中增加边 { CurveFittingEdge* edge = new CurveFittingEdge( x_data[i] ); edge->setId(i); edge->setVertex( 0, v ); // 设置连接的顶点 edge->setMeasurement( y_data[i] ); // 观测数值 edge->setInformation( Eigen::Matrix<double,1,1>::Identity()*1/(w_sigma*w_sigma) ); // 信息矩阵:协方差矩阵之逆 optimizer.addEdge( edge ); } // 第6步:设置优化参数,开始执行优化 optimizer.initializeOptimization(); optimizer.optimize(100);
具体解析:
第一步:创建一个线性求解器LinearSolver
求解增量方程是:H△X=-b,通常是直接求逆。即,△X=H.inv()*(-b)。一般如果H的维度小可以这么做,如果维度大就不能这样做。所以要使用其它的办法来求逆。g2o收集了多种求解方法放在g2o/solvers文件下。

有博主总结了它们的差异:
LinearSolverCholmod :使用sparse cholesky分解法。继承自LinearSolverCCS LinearSolverCSparse:使用CSparse法。继承自LinearSolverCCS LinearSolverPCG :使用preconditioned conjugate gradient 法,继承自LinearSolver LinearSolverDense :使用dense cholesky分解法。继承自LinearSolver LinearSolverEigen: 依赖项只有eigen,使用eigen中sparse Cholesky 求解,因此编译好后可以方便的在其他地方使用,性能和CSparse差不多。继承自LinearSolver
主要是针对不同求逆的办法。
第二步:创建BlockSolver。并用上面定义的线性求解器初始化。
BlockSolver 内部包含 LinearSolver,用上面我们定义的线性求解器LinearSolver来初始化。它的定义在如下文件夹内:g2o/g2o/core/block_solver.h
我下载的这一版g2o全部使用模板类重写了,和之前文章的源码差别好大。。。
template <int p, int l>
using BlockSolverPL = BlockSolver<BlockSolverTraits<p, l>>;
// variable size solver
using BlockSolverX = BlockSolverPL<Eigen::Dynamic, Eigen::Dynamic>;
// solver for BA/3D SLAM
using BlockSolver_6_3 = BlockSolverPL<6, 3>;
// solver fo BA with scale
using BlockSolver_7_3 = BlockSolverPL<7, 3>;
// 2Dof landmarks 3Dof poses
using BlockSolver_3_2 = BlockSolverPL<3, 2>;这里的BlockSolver有两种定义模式,第一种是BlockSolverPL是固定尺度,P表示pose而L表示Landmark。第二种是BlockSolverX是变换尺度,在某些应用场景,我们的Pose和Landmark在程序开始时并不能确定,那么此时这个块状求解器就没办法固定变量,此时使用这个可变尺寸的solver,所有的参数都在中间过程中被确定。
第三步:创建总求解器solver。并从GN, LM, DogLeg 中选一个,再用第二步得到求解器BlockSolver初始化。
还是在g2o/g2o/core文件夹下:
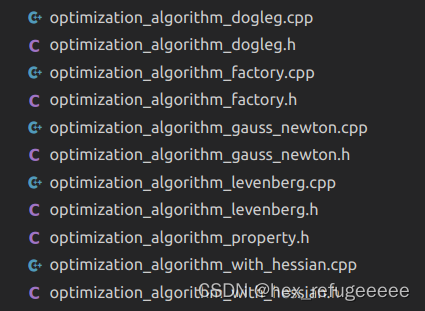
可以看到之间框架图里面提到的三种迭代方法。点开其中一个,就会发现它们都是继承于OptimizationWithHessian类。

这和前面的框架图里面的箭头是匹配的。
第四步:创建核心SparseOptimizer。
g2o::SparseOptimizer optimizer; // 图模型
optimizer.setAlgorithm(solver); // 设置求解器
optimizer.setVerbose(true); // 打开调试输出第五步:添加顶点和边。
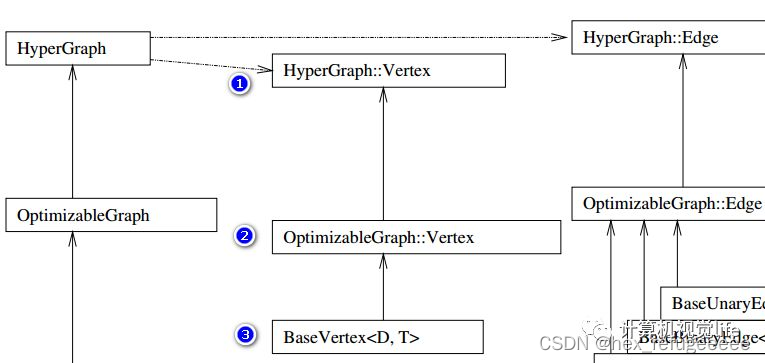
这张图比较清晰,直接看源码,在g2o/core/hyper_graph.h里面是对HyperGraph类的定义。它里面有两个类分别是Vertex和Edge,符合上图关系。里面还涉及了抽象类,简单来说就是如果一个类里面它有一个纯虚函数或则继承的基类是抽象类且没有对虚函数进行定义则它们都是抽象类。
class G2O_CORE_API HyperGraph {
public:
/**
* \brief enum of all the types we have in our graphs
*/
enum G2O_CORE_API HyperGraphElementType {
HGET_VERTEX,
HGET_EDGE,
HGET_PARAMETER,
HGET_CACHE,
HGET_DATA,
HGET_NUM_ELEMS // keep as last elem
};
......
//! abstract Vertex, your types must derive from that one
class G2O_CORE_API Vertex : public HyperGraphElement {
public:
//! creates a vertex having an ID specified by the argument
explicit Vertex(int id = InvalidId);
virtual ~Vertex();
//! returns the id
int id() const { return _id; }
virtual void setId(int newId) { _id = newId; }
//! returns the set of hyper-edges that are leaving/entering in this vertex
const EdgeSet& edges() const { return _edges; }
//! returns the set of hyper-edges that are leaving/entering in this vertex
EdgeSet& edges() { return _edges; }
virtual HyperGraphElementType elementType() const { return HGET_VERTEX; }
protected:
int _id;
EdgeSet _edges;
};
......
class G2O_CORE_API Edge : public HyperGraphElement {
public:
//! creates and empty edge with no vertices
explicit Edge(int id = InvalidId);
virtual ~Edge();
......
}而OptimizableGraph::Vertex is a HyperGraph::Vertex,说明Optimizable::Vertex继承自HyperGraph::Vertex,源码中也是这样的。
struct G2O_CORE_API OptimizableGraph : public HyperGraph {
enum ActionType {
AT_PREITERATION,
AT_POSTITERATION,
AT_NUM_ELEMENTS, // keep as last element
};
......
class G2O_CORE_API Vertex : public HyperGraph::Vertex,
public HyperGraph::DataContainer {
private:
friend struct OptimizableGraph;
......
}最后是使用最多的BaseVertex,它在这里g2o/core/base_vertex.h,也是继承自OptimizableGraph::Vertex。
/**
* \brief Templatized BaseVertex
*
* Templatized BaseVertex
* D : minimal dimension of the vertex, e.g., 3 for rotation in 3D. -1 means
* dynamically assigned at runtime. T : internal type to represent the
* estimate, e.g., Quaternion for rotation in 3D
*/
template <int D, typename T>
class BaseVertex : public OptimizableGraph::Vertex {
public:
typedef T EstimateType;
typedef std::stack<
EstimateType,
std::vector<EstimateType, Eigen::aligned_allocator<EstimateType> > >
BackupStackType;D代表了vertex的最小维度,比如3D空间中旋转是3维的,那么这里 D = 3。
T表示待估计vertex的数据类型,比如用四元数表达三维旋转的话,T就是Quaternion 类型。
static const int Dimension = D;
///< dimension of the estimate (minimal) in the manifold space typedef T EstimateType;
EstimateType _estimate;g2o提供了一批已经定义好的定点:
VertexSE2 : public BaseVertex<3, SE2> //2D pose Vertex, (x,y,theta) VertexSE3 : public BaseVertex<6, Isometry3> //6d vector (x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion) VertexPointXY : public BaseVertex<2, Vector2> VertexPointXYZ : public BaseVertex<3, Vector3> VertexSBAPointXYZ : public BaseVertex<3, Vector3> // SE3 Vertex parameterized internally with a transformation matrix and externally with its exponential map VertexSE3Expmap : public BaseVertex<6, SE3Quat> // SBACam Vertex, (x,y,z,qw,qx,qy,qz),(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion. // qw is assumed to be positive, otherwise there is an ambiguity in qx,qy,qz as a rotation VertexCam : public BaseVertex<6, SBACam> // Sim3 Vertex, (x,y,z,qw,qx,qy,qz),7d vector,(x,y,z,qx,qy,qz) (note that we leave out the w part of the quaternion. VertexSim3Expmap : public BaseVertex<7, Sim3>
如果没有,也可以自行定义,但要重写这些函数:
virtual bool read(std::istream& is); virtual bool write(std::ostream& os) const; virtual void oplusImpl(const number_t* update); virtual void setToOriginImpl();
read,write:分别是读盘、存盘函数,一般情况下不需要进行读/写操作的话,仅仅声明一下就可以。
setToOriginImpl:顶点重置函数,设定被优化变量的原始值。
oplusImpl:顶点更新函数。非常重要的一个函数,主要用于优化过程中增量△x 的计算。我们根据增量方程计算出增量之后,就是通过这个函数对估计值进行调整的,因此这个函数的内容一定要重视。
举例:
class myVertex: public g2::BaseVertex<Dim, Type>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
myVertex(){}
virtual void read(std::istream& is) {}
virtual void write(std::ostream& os) const {}
virtual void setOriginImpl()
{
_estimate = Type();
}
virtual void oplusImpl(const double* update) override
{
_estimate += /*update*/;
}
}这是一个自己定义的顶点的格式,符合前面所有的要求,这里的增量是相加的。又比如高博g2o的内容:
class CurveFittingVertex : public g2o::BaseVertex<3, Eigen::Vector3d> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
// 重置
virtual void setToOriginImpl() override {
_estimate << 0, 0, 0;
}
// 更新
virtual void oplusImpl(const double *update) override {
_estimate += Eigen::Vector3d(update);
}
// 存盘和读盘:留空
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
};这里也是因为它是向量,所以也是可以相加的。但遇到不能相加的,李代数的例子。比如:
g2o/types/sba/types_six_dof_expmap.h
/**
\* \brief SE3 Vertex parameterized internally with a transformation matrix
and externally with its exponential map
*/
class G2O_TYPES_SBA_API VertexSE3Expmap : public BaseVertex<6, SE3Quat>{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
VertexSE3Expmap();
bool read(std::istream& is);
bool write(std::ostream& os) const;
virtual void setToOriginImpl() {
_estimate = SE3Quat();
}
virtual void oplusImpl(const number_t* update_) {
Eigen::Map<const Vector6> update(update_);
setEstimate(SE3Quat::exp(update)*estimate()); //更新方式
}
};其中6表示内部存储的优化变量维度,这是个6维的李代数。SE3Quat是优化变量的类型,是g2o定义的相机位姿类型。这里就不能相加,因为传递矩阵没有加法,要采用别的更新办法。
将顶点的数据格式定义好了后,添加顶点的操作就比较简单了,还是以高博的代码为例:
CurveFittingVertex* v = new CurveFittingVertex();
v->setEstimate( Eigen::Vector3d(0,0,0) );
v->setId(0);
optimizer.addVertex( v );CurveFittingVertex是自己定义的顶点的类,然后就是初始化的操作,最后就是直接optimizer.addVertex(v)来添加顶点。
关于边Edge,这里就不去查看它们源码之间的继承关系了,按框架图中的表示就可以了。
BaseUnaryEdge,BaseBinaryEdge,BaseMultiEdge 分别表示一元边,两元边,多元边
一元边可以理解为一条边只连接一个顶点,两元边理解为一条边连接两个顶点,多元边理解为一条边可以连接多个(3个以上)顶点。
相关参数:
D 是 int 型,表示测量值的维度 (dimension)
E 表示测量值的数据类型
VertexXi,VertexXj 分别表示不同顶点的类型
BaseBinaryEdge<2, Vector2D, VertexSBAPointXYZ, VertexSE3Expmap>首先这个是个二元边。第1个2是说测量值是2维的,也就是图像像素坐标x,y的差值,对应测量值的类型是Vector2D,两个顶点也就是优化变量分别是三维点 VertexSBAPointXYZ,和李群位姿VertexSE3Expmap。
然后是自己定义边的需要写的函数:
virtual bool read(std::istream& is);
virtual bool write(std::ostream& os) const;
virtual void computeError();
virtual void linearizeOplus();read,write:分别是读盘、存盘函数,一般情况下不需要进行读/写操作的话,仅仅声明一下就可以。
computeError函数:非常重要,是使用当前顶点的值计算的测量值与真实的测量值之间的误差。
linearizeOplus函数:非常重要,是在当前顶点的值下,该误差对优化变量的偏导数,也就是我们说的Jacobian。
还有一些比较重要的:
_measurement:存储观测值
_error:存储computeError() 函数计算的误差
_vertices[]:存储顶点信息,比如二元边的话,_vertices[] 的大小为2,存储顺序和调用setVertex(int, vertex) 是设定的int 有关(0 或1)
setId(int):来定义边的编号(决定了在H矩阵中的位置)
setMeasurement(type) 函数来定义观测值
setVertex(int, vertex) 来定义顶点
setInformation() 来定义协方差矩阵的逆模板:
class myEdge: public g2o::BaseBinaryEdge<errorDim, errorType, Vertex1Type, Vertex2Type>
{
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
myEdge(){}
virtual bool read(istream& in) {}
virtual bool write(ostream& out) const {}
virtual void computeError() override
{
// ...
_error = _measurement - Something;
}
virtual void linearizeOplus() override
{
_jacobianOplusXi(pos, pos) = something;
// ...
/*
_jocobianOplusXj(pos, pos) = something;
...
*/
}
private:
// data
}实际例子,还是使用高博的源码。
// 误差模型 模板参数:观测值维度,类型,连接顶点类型
class CurveFittingEdge : public g2o::BaseUnaryEdge<1, double, CurveFittingVertex> {
public:
EIGEN_MAKE_ALIGNED_OPERATOR_NEW
CurveFittingEdge(double x) : BaseUnaryEdge(), _x(x) {}
// 计算曲线模型误差
virtual void computeError() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
_error(0, 0) = _measurement - std::exp(abc(0, 0) * _x * _x + abc(1, 0) * _x + abc(2, 0));
}
// 计算雅可比矩阵
virtual void linearizeOplus() override {
const CurveFittingVertex *v = static_cast<const CurveFittingVertex *> (_vertices[0]);
const Eigen::Vector3d abc = v->estimate();
double y = exp(abc[0] * _x * _x + abc[1] * _x + abc[2]);
_jacobianOplusXi[0] = -_x * _x * y;
_jacobianOplusXi[1] = -_x * y;
_jacobianOplusXi[2] = -y;
}
virtual bool read(istream &in) {}
virtual bool write(ostream &out) const {}
public:
double _x; // x 值, y 值为 _measurement
};雅克比矩阵是用来求解误差的。
然后就是添加边,比较简单:
// 往图中增加边
for (int i = 0; i < N; i++) {
CurveFittingEdge *edge = new CurveFittingEdge(x_data[i]);
edge->setId(i);
edge->setVertex(0, v); // 设置连接的顶点
edge->setMeasurement(y_data[i]); // 观测数值
edge->setInformation(Eigen::Matrix<double, 1, 1>::Identity() * 1 / (w_sigma * w_sigma)); // 信息矩阵:协方差矩阵之逆
optimizer.addEdge(edge);
}这是添加一个顶点,v是前面生成的顶点。
还有一个两元边的例子。
index = 1;
for ( const Point2f p:points_2d )
{
g2o::EdgeProjectXYZ2UV* edge = new g2o::EdgeProjectXYZ2UV();
edge->setId ( index );
edge->setVertex ( 0, dynamic_cast<g2o::VertexSBAPointXYZ*> ( optimizer.vertex ( index ) ) );
edge->setVertex ( 1, pose );
edge->setMeasurement ( Eigen::Vector2d ( p.x, p.y ) );
edge->setParameterId ( 0,0 );
edge->setInformation ( Eigen::Matrix2d::Identity() );
optimizer.addEdge ( edge );
index++;
}这里的0和1分别代表了不同的顶点。0表示的是VertexSBAPointXYZ 类型的顶点,1对应的是VertexSE3Expmap 类型的顶点就是位姿pose。g2o不会区分顶点的类型需要自己区分。
这里准备一个练习,使用g2o完成一次优化,把上面提到的流程走一遍。
图优化数学理论
四、图优化理论来源
主要学习高博的两篇博客:文章一、文章二。两篇博客写的非常详细,这里作一些简单的笔记。
优化理论前提:
优化问题有三个最重要的因素:目标函数、优化变量、优化约束。一个简单的优化问题可以描述如下:
其中x为优化变量,而F(x)是优化函数。此问题是无优化问题,因为没有任何约束形式,而slam中大多数都是无约束的优化问题。当F(x)有特殊性质时,对应的优化问题也可以用一些特殊的解法。例如,当F(x)为一个线性函数时,则为线性优化问题。反之为非线性优化,对于无约束的非线性优化,如果我们知道它梯度的解析形式,就能直接求那些梯度为零的点,来解决这个优化:
梯度为零的地方可能是函数的极大值、极小值或者鞍点。但不知道F(x)的形式,就遍历所有的极值点,找到最小的作为最优解。但并不是所有的工程问题都可以得到具体的F(x)的解析式。所以一般使用迭代的方法求解。包括梯度下降法,反复迭代,直到求出最优解。一般有两种迭代方法:Gauss-Newton (GN)法和 Levenberg-Marquardt (LM)法。
slam问题和图相结合:
slam的核心根据已有的观测数据,计算机器人的运动轨迹和地图。
假设在时刻k,机器人在位置处,用传感器进行了一次观测,得到了数据
。传感器的观测方程为:
算上误差:
以为优化变量,以
为目标函数,就可以求出
的估计值。
观测方程有多种形式:
- 机器人两个Pose之间的变换;
- 机器人在某个Pose处用激光测量到了某个空间点,得到了它离自己的距离与角度;
- 机器人在某个Pose处用相机观测到了某个空间点,得到了它的像素坐标;
与图相结合:
在图中,以顶点表示优化变量,以边表示观测方程。由于边可以连接一个或多个顶点,所以我们把它的形式写成更广义的 ,以表示不限制顶点数量的意思。而上面提到的三种观测方程就表示为:
机器人两个Pose之间的变换;——一条Binary Edge(二元边),顶点为两个pose,边的方程为,这也是边的约束方程。
机器人在某个Pose处用激光测量到了某个空间点,得到了它离自己的距离与角度;——Binary Edge,顶点为一个2D Pose:和一个Point:
,观测数据是距离r和角度b,那么观测方程为:
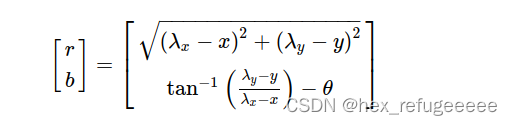
第三个类似。
然后这是没有带上误差的理想情况,而优化的主要任务就是算出优化变量误差最小。
接下来的内容全是公式推导,建议直接看原文,讲的很清楚,csdn上面实在是不好处理公式。我在纸上推导了一遍。
最后可以得到最开始要求进行g2o的那个公式:。直接跟着上面的流程走就行了。
高博直接帮我们总结了:
小结
最后总结一下做图优化的流程。
- 选择你想要的图里的节点与边的类型,确定它们的参数化形式;
- 往图里加入实际的节点和边;
- 选择初值,开始迭代;
- 每一步迭代中,计算对应于当前估计值的雅可比矩阵和海塞矩阵;
- 求解稀疏线性方程HkΔx=−bk,得到梯度方向;
- 继续用GN或LM进行迭代。如果迭代结束,返回优化值。
实际上,g2o能帮你做好第3-6步,你要做的只是前两步而已。下节我们就来尝试这件事。
五、g2o使用实例
在这里直接看了下任佬的关于g2o的源码,然后发现对于我来说好复杂,好像刚刚弄明白1+1 = 2,突然就要算两位数的乘法了(还是太菜了)。然后我在网上又找到一篇讲的特别好的,还没发现讲的比这篇文章还要清晰的入门g2o的文章:文章。
总结的特别好,这篇文章的作者完成了这篇文章举的第一个例子,我在他的代码上更换了几个数据就直接算出了第二个例子的数值。

答案数值:
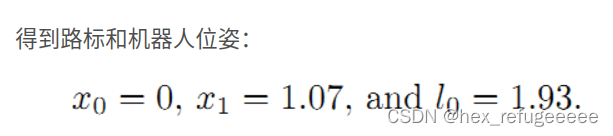
所以对于g2o来说,将点和边的定义设置好就让它直接帮你算出结果。
发现使用g2o最难的可能是对应版本的问题,解决库的问题真的好复杂。。。先记录到这里







![[2022-11-28]神经网络与深度学习 hw10 - LSTM和GRU](https://img-blog.csdnimg.cn/67bd25358cf84ae79f453a4079fec999.png#pic_center)
