💥💥💞💞欢迎来到本博客❤️❤️💥💥
🏆博主优势:🌞🌞🌞博客内容尽量做到思维缜密,逻辑清晰,为了方便读者。
⛳️座右铭:行百里者,半于九十。
📋📋📋本文目录如下:🎁🎁🎁
目录
💥1 概述
📚2 运行结果
🎉3 参考文献
🌈4 Matlab代码实现
💥1 概述

本研究提出了一种新的元启发式算法,称为沙猫群优化(SCSO),该算法模拟了试图在自然界中生存的沙猫行为。这些猫能够检测到低于 2 kHz 的低频,并且还具有令人难以置信的挖掘猎物的能力。受这两个特征的启发,所提出的算法由两个主要阶段(搜索和攻击)组成。该算法以平衡的方式控制勘探和开发阶段的过渡,在以较少的参数和操作找到良好的解决方案方面表现良好。它是通过使用定义的自适应策略找到适当运动的方向和速度来实现的。将SCSO算法与CEC20基准函数的10个知名复数测试函数以及现代2019个复杂测试函数进行了测试,并将获得的结果与著名的元启发式算法进行了对比。根据结果,在63.3%的测试函数中找到最佳解的算法是SCSO。此外,SCSO算法还应用于焊接梁设计、拉伸/压缩弹簧设计、压力容器设计、活塞杠杆、减速器设计、三杆桁架设计和悬臂梁设计等<>个具有挑战性的工程设计问题。结果表明,SCSO在收敛率和定位全部或大部分局部/全局最优方面表现良好,优于其他比较方法。
在现实生活中,优化意味着除了最大限度地提高效率和质量外,还意味着最大限度地减少时间和成本。事实上,有很多问题需要优化,既复杂又困难。启发式和元启发式算法是解决问题和获得优化解决方案的两种方法。启发式算法是问题依赖性的,而元启发式算法不依赖于特定问题,最优解是从随机搜索空间和预定义边界[1]中获得的。问题越大越复杂,解决起来就越困难[2]。特别是他们的时间和记忆复杂性会显着恶化。这些类型的问题中最突出的是非确定性多项式时间(NP-hard)问题。NP-hard问题可以通过精确和近似的方法解决。精确的方法保证了具有指数级时间复杂度和高成本的最佳解决方案。启发式算法和元启发式算法都是近似算法的家族,不能保证找到最优解,但得到的解可能更接近最优解,复杂度和实际执行时间更好。因此,第二组通常是首选。另一方面,考虑到启发式方法存在局部陷阱等问题,元启发式方法可以为许多NP难题提供实用且有用的解决方案,并且在实际执行时间内为这些类型的问题找到最优解方面通常表现良好[3]。
元启发式方法不会落入局部陷阱,此外,它们更加灵活,并试图通过简单的实施在更短的时间内以更少的流程成本在全球搜索领域找到最佳解决方案。特别是,元启发式算法的性能可以更成功地解决复杂问题[2]。此外,无免费午餐(NFL)[4]断言没有特定的算法为每个优化问题提供最佳解决方案。因此,开发可用于各种问题的新元启发式算法的需求很大。因此,由于其广泛的使用领域和优势,近年来,元启发式优化算法在许多科学领域变得流行[5,6,7]。一般来说,元启发式算法受到生物或物理现象[8]的启发,并试图在合理的时间内找到最佳解决方案(最大值或最小值)。
元启发式算法通常分为单解算法和基于群体(多)算法两类。在单解算法中,虽然单个解会影响输出,但整个总体都包含在基于总体的算法中。此外,元启发式算法分为进化算法、基于物理算法和群体智能算法。进化算法(EA)的灵感来自自然进化论和达尔文进化论[9]。EA 在随机搜索空间内解决问题,而 EA 是一种基于群体的方法,其中整个总体影响最佳解决方案。遗传算法 (GA) 是 EA 类别 [10] 中众所周知的算法,其灵感来自世代复制。GA 通过模仿交叉、突变和精英主义来产生新一代,以找到全局最优。差分进化(DE)算法是另一种受自然进化驱动的算法。DE算法在生成下一代的选择操作中与GA有所不同[11]。改进的量子衍生合作协同进化算法(MSQCCEA)[12]是目前的研究之一。该算法提高了全局搜索能力,不会落入局部最优陷阱。因此,已经开发出一种量子自旋方向策略,将量子演化方向从13个变为14个。将该方法应用于背包和实际机场登机口分配问题,结果表明所提算法在快速、准确的收敛速率方面具有良好的性能。禁忌搜索(TS)算法是进化算法的另一个例子[15]。进化编程(EP)的灵感来自表型、遗传和变异等行为模型[16]。基于生物地理学的优化器(BBO)[<>]和黑寡妇优化(BWO)[<>]是EA的另一个例子。
基于物理的算法是元启发式方法的另一个家族成员。这些算法受到自然界物理规则的启发,并根据假设的物理事件随机行动。在这种算法中,搜索空间和最优解遵循电磁力、引力和惯性力等物理规律。这一类别中有著名的优化算法,如引力局部搜索(GLSA)[17],引力搜索算法(GSA)[18]和大爆炸-大紧缩(BBBC)[19]。黑洞(BH)算法的灵感来自黑洞现象的事实[20],是基于物理学的另一种算法。该类别中的其他著名作品是带电系统搜索(CSS)[21],曲线空间优化[22],中心力优化(CFO)[23]和基于星系的搜索算法(GbSA)[24]。在此类别的方法中,搜索代理根据假定的物理事件随机操作。
群体智能(SI)是元启发式算法的第三类。通常,SI方法的灵感来自自然界中成群,饲养和成群的动物的社会行为。在这种算法中,搜索代理试图通过影响社交智能来找到最佳解决方案。粒子群优化(PSO)是这一类别中最著名的算法[25]。PSO的灵感来自鸟类在自然界中的运动和社会行为。粒子指示候选解决方案,算法尝试根据这些粒子从搜索空间中找到最佳解决方案。蚁群优化(ACO)是该类别中的另一种算法[26]。ACO算法模拟蚂蚁的觅食行为。自然界中蚂蚁的主要目标是找到目的地(食物)并在源头和目的地之间生成最佳(安全和最低成本)路径。在文献中,该算法已被用于解决许多类型的问题[27,28]。人工蜂群(ABC)[29]算法是另一种模仿蜜蜂社会行为的重要算法。在ABC发现中,在目的地(巢)和源(食物)之间生成了一条路径。寻找丰富的食物资源和蜜蜂体验是ABC算法中寻找最佳解决方案的重要阶段。此类别中的其他算法包括蝙蝠算法 (BA) [30]、萤火虫算法 (FA) [31]、灰狼优化 (GWO) [32] 和不同方差 [33]、鲸鱼优化算法 (WOA) [34]、蜻蜓算法 (DA) [35]、布谷鸟搜索 (CS) [36]、蝴蝶优化算法 (BOA) [37]、风驱动优化 (WDO) [38]、猫群优化 (CSO) [39],果蝇优化算法(FFOA)[40]和花授粉算法(FPA)[41],Salp群算法(SSA)[42],探路者算法(PFA)[43]及其改进版本[3],以及哈里斯鹰优化(HHO)算法[44]。此外,混合元启发式算法近年来已经变得普遍。[45,46]介绍了在这种情况下所做的两项有价值的研究。在[45]中,作者提出了一种基于DA和WDO算法的新方法。作者纠正了这两种算法的缺点,并因此证明了他们提出的方法具有快速的收敛速度和强大的全局搜索能力,并且在寻找解决方案方面是准确的。在[46]中,作者受到BOA和FPA算法的启发,提出了一种灵活的算法来解决全局优化问题。作者提出了一种在探索和开发阶段之间有效切换的新机制,因此该算法表现出平衡的行为。
元启发式算法的主要阶段是探索和开发,每种算法都有特定的策略来实现这些阶段的概念。所提出的算法中这两个阶段之间的平衡越多,成功率就越高。在这些策略中,定义的随机性和适当的系数很重要。正确设置相关系数参数以确保这两个相位之间的良好平衡非常重要[33]。探索意味着在全球范围内进行搜索。此阶段需要更多的搜索,因此相关算法从搜索空间中随机选择一个解决方案。而开发阶段在探索阶段之后,而开发阶段侧重于搜索空间上的解决方案以改进解决方案。换句话说,检查未访问的区域是否是局部最优差的潜在逃生区域。探索中搜索的随机性会影响算法,以避免在探索全局最优的局部最优上陷害。
本文提出了一种新的元启发式优化算法,该算法可能更适合于根据NFL定理解决相关阶段之间表现平衡的各种问题。此外,所提出的算法比目前其他元启发式算法具有更有利的复杂性。该算法受沙猫搜索和狩猎行为的启发,命名为沙猫群优化(SCSO)。沙猫在自然界中独居,但在所提出的算法中,沙猫被认为是一个可以被用户识别为搜索代理的群体。在所提算法的开发中,重点是沙猫寻找猎物的低频噪声检测行为。这些猫检测到低于 2 kHz 的低频,因此它们可以在可能的短时间内长距离捕捉猎物,而且几乎没有动作。此外,沙猫具有令人难以置信的挖掘猎物的能力。由于这两个奇妙的功能,确保了沙猫在自然界中具有搜索和狩猎的特殊能力。所提出的算法在探索和开发阶段也通过自适应机制保持平衡。此外,本文的主要贡献总结如下。
1.两个阶段:搜索和攻击猎物。本文提出的算法(SCSO)就包括了这两个阶段,此外,还提出了一种机制来实现探索和利用阶段的平衡。
2.算法运行时首先根据问题的规模( N pop × N d ) , ( pop = 1 , . . . , n =1,…,n=1,…,n)利用沙丘猫群创建一个候选矩阵,然后就目标函数对每个沙丘猫进行适应度评估,选择出其中最优的个体,其他的个体都朝向该个体移动。
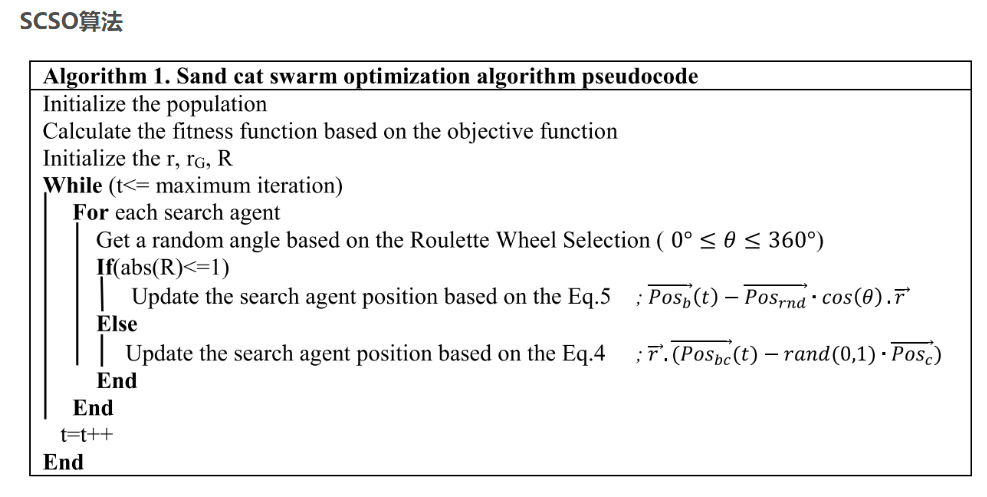
详细数学模型和文章见参考文献。
📚2 运行结果
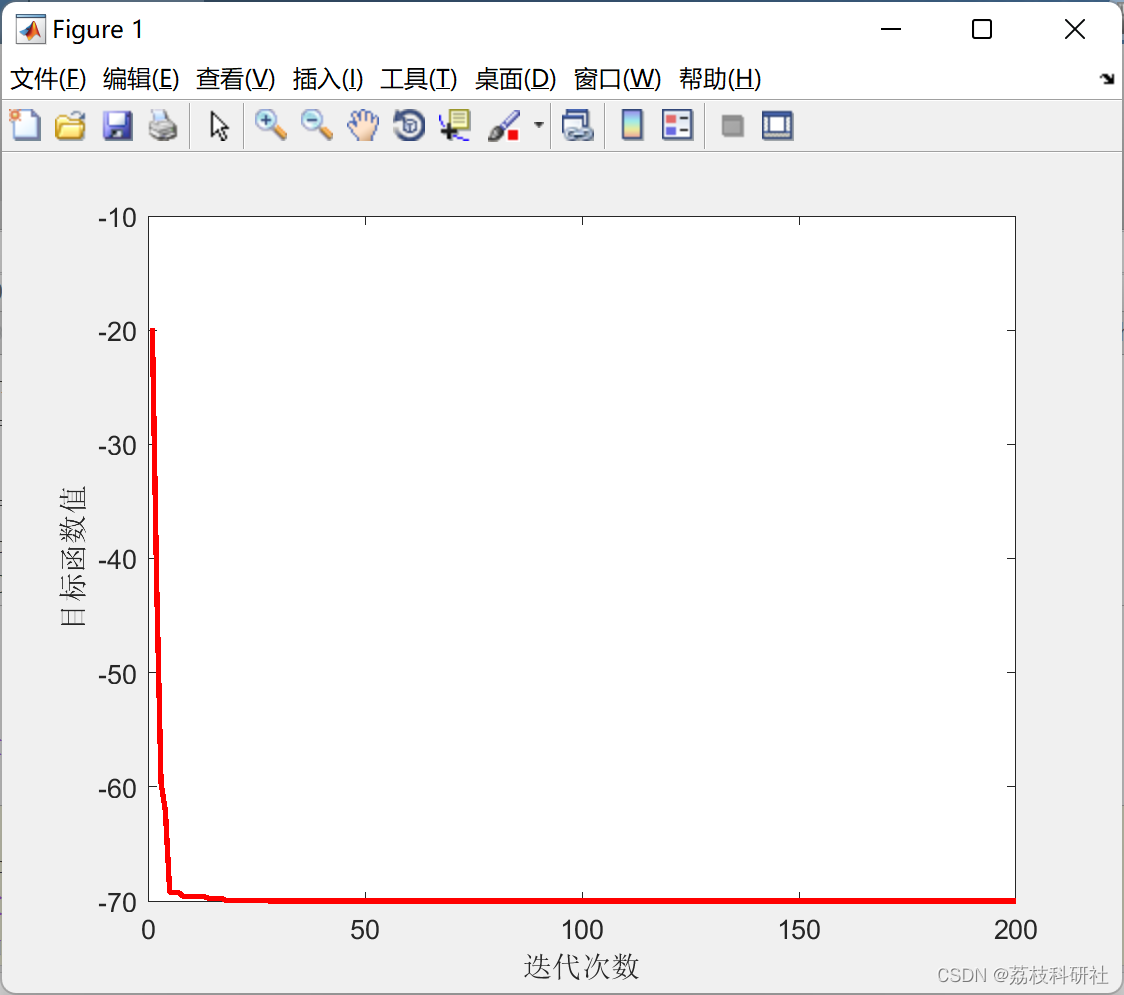
部分代码:
function [Best_Score,BestFit,Convergence_curve]=SCSO(SearchAgents_no,Max_iter,lb,ub,dim,fobj)
BestFit=zeros(1,dim);
Best_Score=inf;
Positions=initialization(SearchAgents_no,dim,ub,lb);
Convergence_curve=zeros(1,Max_iter);
t=0;
p=[1:360];
while t<Max_iter
for i=1:size(Positions,1)
Flag4ub=Positions(i,:)>ub;
Flag4lb=Positions(i,:)<lb;
Positions(i,:)=(Positions(i,:).*(~(Flag4ub+Flag4lb)))+ub.*Flag4ub+lb.*Flag4lb;
fitness=fobj(Positions(i,:));
if fitness<Best_Score
Best_Score=fitness;
BestFit=Positions(i,:);
end
end
S=2; %%% S is maximum Sensitivity range
rg=S-((S)*t/(Max_iter)); %%%% guides R
for i=1:size(Positions,1)
r=rand*rg;
R=((2*rg)*rand)-rg; %%%% controls to transtion phases
for j=1:size(Positions,2)
teta=RouletteWheelSelection(p);
if((-1<=R)&&(R<=1)) %%%% R value is between -1 and 1
Rand_position=abs(rand*BestFit(j)-Positions(i,j));
Positions(i,j)=BestFit(j)-r*Rand_position*cos(teta);
else
cp=floor(SearchAgents_no*rand()+1);
CandidatePosition =Positions(cp,:);
Positions(i,j)=r*(CandidatePosition(j)-rand*Positions(i,j));
end
end
end
t=t+1;
Convergence_curve(t)=Best_Score;
end
end
🎉3 参考文献
部分理论来源于网络,如有侵权请联系删除。
[1]Seyyedabbasi, A., Kiani, F. Sand Cat swarm optimization: a nature-inspired algorithm to solve global optimization problems. Engineering with Computers (2022).
[2]高烨,陶丽丽,马苗.基于猫群优化算法的图像多阈值分割方法[J].中国体视学与图像分析,2018,23(02):125-132.DOI:10.13505/j.1007-1482.2018.23.02.001.
[3]姜天华.猫群优化算法求解柔性作业车间调度问题[J].计算机工程与应用,2018,54(23):259-263+270.