全部学习汇总: GreyZhang/python_basic: My learning notes about python. (github.com)
最初接触递归的时候觉得这个有点不好理解,怎么能够有这种思维方式?这完全不同于之前自己所能够了解的那种一加一等于二的方式。相对于能够看得见的那种直观的理论,这些确实是一种逻辑型的、推理式的描述理论。
递推比较适合解决的问题通常有两个特点:第一,需要解决的复杂问题可以分解或者简化为更小或者更简单的小问题;第二,最小或者最简单的问题能够得出确切的答案。
从之前实现的一个问题来入手说明一下,如果想要求解a*b,在之前的循环中采用的解决方式如下:
a * b = a + a +......+a(b个a)。
如果把上面的公式变化一下,改成:
a *b = a + a + …… + a(b-1个a) + a
以上的描述依然成立,但是右边部分可以理解为a * (b - 1) + a
假设有一个函数f(x) = ax来描述上面的表达,那么a *b 可以理解为f(b)的函数值。而第二个表达式则可以理解为f(b-1) + a的值。而对于f(x)来说,f(x) = f(x-1) + a也是成立的。对于这种描述成立的证明,通常可以使用数学归纳法来证明。证明的过程一般是先验证最初的几个比较小的数值,再假设x = k的时候成立,推导出x = k + 1的时候依然成立。
既然有了上面f(x) = f(x-1) + a的推导关系,而x=1的时候结果我们显然知道。那么求解相应计算的函数可以设计如下:

执行结果如下:
>>> ================================ RESTART ================================
>>>
>>> F(3,5)
15
>>> F(123,456)
56088
通过以上的演示可以看出,在一定范围内的问题处理分析使用递归的思想是可以化繁为简、化腐朽为神奇的。
在程序设计上,个人感觉循环和递归之间很多时候都是可以相互转化的。倒不是说这两种方式等同,只是说能够解决同样的问题。但是在编程实践中发现,递归的方式通常会消耗大量的内存。一般的代码中,递归的嵌套层级也是有限制的。当嵌套的数目过多,程序无法执行。单纯的循环这方面的限制则会少很多。不过,很多时候,递归的方式确实是能够写出更加简洁的代码。如果运算的层级不深,倒是一种不错的选择方式。
常见的递归算法示例莫过于那几个,最常见的便是汉诺塔以及斐波那契函数。下面也写几个简单的递归函数,加深一下印象。
示例1:求阶乘
代码设计如下:
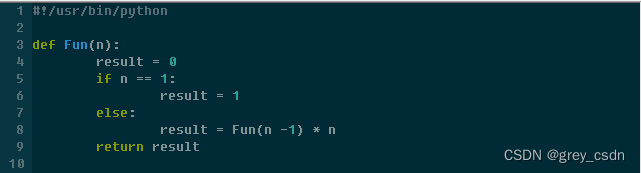
执行结果如下:
>>> ================================ RESTART ================================
>>>
>>> Fun(1)
1
>>> Fun(5)
120
>>> Fun(20)
2432902008176640000L
通过测试,执行结果正确。
示例2:汉诺塔
设计代码如下:

运行测试结果如下:
>>> ================================ RESTART ================================
>>>
>>> Towers(1,'A','B','C')
move from A to B
>>> Towers(2,'A','B','C')
move from A to C
move from A to B
move from C to A
>>> Towers(5,'A','B','C')
move from A to B
move from A to C
move from B to A
move from A to B
move from C to B
move from C to A
move from B to C
move from A to C
move from B to A
move from B to C
move from A to B
move from B to A
move from C to A
move from C to B
move from A to C
move from A to B
move from C to B
move from C to A
move from B to C
move from C to B
move from A to B
move from A to C
move from B to A
move from C to A
move from B to C
move from B to A
move from C to B
move from B to C
move from A to C
move from A to B
move from C to A
示例3:斐波那契数列
设计代码如下:

运行结果如下:
>>> ================================ RESTART ================================
>>>
>>> Fibnacci(1)
1
>>> Fibnacci(0)
1
>>> Fibnacci(13)
377
>>> Fibnacci(25)
121393
这里特意尝试试了一个比较多层的运算,运算报错,在一大堆的提示后面有一个错误的描述:
RuntimeError: maximum recursion depth exceeded
递归或者迭代的层级超限。这就是前面说到的缺点了。其实,除了这个缺点以外,还有一个比较大的缺点便是执行速度。通常递归的运算在层级比较深的时候慢到足以用需要人来久久等待,通过一个简单的循环计算阶乘的算法比较一下就能够很明显感觉出这种差异。不过,递归确实是一种很好的计算机思维,就像前面所说,很多时候它能够化繁为简。用到合适的地方,这确实是一个简单而有效的方式。