1.问题

序列化是将一个数据结构或者对象转换为连续的比特位的操作，进而可以将转换后的数据存储在一个文件或者内存中，同时也可以通过网络传输到另一个计算机环境，采取相反方式重构得到原数据。

请设计一个算法来实现二叉树的序列化与反序列化。这里不限定你的序列 / 反序列化算法执行逻辑，你只需要保证一个二叉树可以被序列化为一个字符串并且将这个字符串反序列化为原始的树结构。

提示: 输入输出格式与 LeetCode 目前使用的方式一致，详情请参阅 LeetCode 序列化二叉树的格式。你并非必须采取这种方式，你也可以采用其他的方法解决这个问题。

示例 1

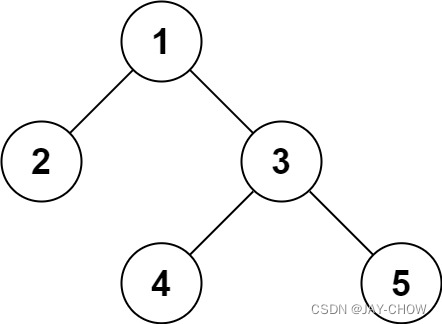
输入：root = [1,2,3,null,null,4,5]
输出：[1,2,3,null,null,4,5]

示例 2

输入：root = []
输出：[]

示例 3

输入：root = [1]
输出：[1]

示例 4

输入：root = [1,2]
输出：[1,2]

提示：

• 树中结点数在范围 [0, 104] 内
• -1000 <= Node.val <= 1000

2.解题思路

二叉树有很多种遍历思路，如要解决本题，可以参考以下二叉树的遍历算法，序列化不用多说，反序列化就是逆向思考之前是怎么序列化的。本章主要讲解怎么利用层序遍历的思想解决反序列化问题。

二叉树遍历系列

• 144.二叉树的前序遍历
• 94.二叉树的中序遍历
• 145.二叉树的后续遍历
• 102.二叉树的层序遍历
• 107.二叉树的层序遍历II
• 103.二叉树的锯齿形层序遍历（之字形遍历）
• 199.二叉树的右视图

---

2.1 BFS

在102.二叉树的层序遍历一文中，我们利用队列的性质对二叉树进行了层序遍历，本章，在序列化时我们也可以用队列，只是不需要分层标识，比如我们可以把它看成是这样：

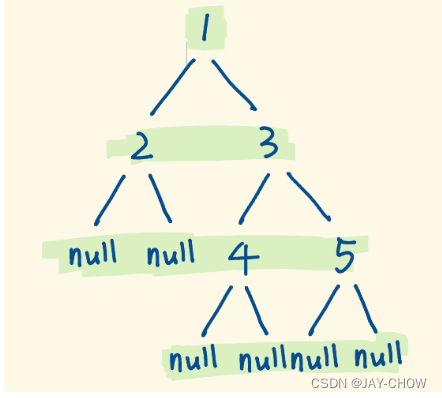
我们定义一个空节点，用以标识某个节点无左或右子节点。用下划线分割各个节点的值。

int INF = -2000;
TreeNode emptyNode = new TreeNode(INF);

则序列化后的结果为：1_2_3_-2000_-2000_4_5_-2000_-2000_-2000_-2000;
反序列化时，利用队列，弹出头结点，包装成二叉树节点，对于序列化的序列，取出两个节点，只要值不是-2000，就可以将父子节点进行关联，再入队，依次循环。

2.2 递归

这里以前序遍历思想为例，其他中序、后序遍历类似。
同样，利用上述2.1节中的自定义空节点标识二叉树的空子节点。序列化伪代码大致如下：

String serialize(TreeNode root){
	if (root == null) {
		return INF;
	}
	//左节点
	String left=serialize(root.left);
	//右节点
	String right=serialize(root.right);
	return root.val+"_"+left.val+"_"+right.val;
}

反序列化

TreeNode deserialize(String str){
	//分离节点值
	ss=str.split("_");
	//递归反序列化
	return buildTree(ss);
}

TreeNode buildTree(ss){
	//弹出第一个value
	value=ss.poll();
	//非自定义空节点 递归
	if(value==INF){
		return null;
	}
	//构造节点
	TreeNode root=new TreeNode(value);
	root.left=buildTree(ss);
	root.right=buildTree(ss);
	return root;
}

3.代码

import java.util.ArrayDeque;
import java.util.Deque;
/*
public class TreeNode {
    int val = 0;
    TreeNode left = null;
    TreeNode right = null;

    public TreeNode(int val) {
        this.val = val;

    }

}
*/
public class Solution {
	//定义空节点的值
    int INF = -2000;
    TreeNode emptyNode = new TreeNode(INF);

	//BFS
    String Serialize(TreeNode root) {
        if (root == null) {
        	return "";
        }
		//序列化的临时结果
        StringBuilder sb = new StringBuilder();
        Deque<TreeNode> d = new ArrayDeque<>();
        d.addLast(root);
        while (!d.isEmpty()) {
        	//弹出一个节点，第一个是root
            TreeNode poll = d.pollFirst();
            //序列化的值以下划线分割
            sb.append(poll.val + "_");
            //非自定义的空节点关联父节点
            if (!poll.equals(emptyNode)) {
                d.addLast(poll.left != null ? poll.left : emptyNode);
                d.addLast(poll.right != null ? poll.right : emptyNode);
            }
        }
        System.out.println(sb.toString());
        return sb.toString();
    }

    //BFS
    TreeNode Deserialize(String data) {
        if (data.equals("")) {
        	return null;
        }

        String[] ss = data.split("_");
        int n = ss.length;
        //根节点
        TreeNode root = new TreeNode(Integer.parseInt(ss[0]));
        Deque<TreeNode> d = new ArrayDeque<>();
        d.addLast(root);
        for (int i = 1; i < n - 1; i += 2) {
            TreeNode poll = d.pollFirst();
            int a = Integer.parseInt(ss[i]);
            int b = Integer.parseInt(ss[i + 1]);
            //非自定义空节点的值，包装成二叉树的节点，关联上父节点
            if (a != INF) {
                poll.left = new TreeNode(a);
                d.addLast(poll.left);
            }
            if (b != INF) {
                poll.right = new TreeNode(b);
                d.addLast(poll.right);
            }
        }
        return root;
    }

	//递归序列化和反序列化
	//前序遍历
    String Serialize2(TreeNode root) {
        if (null == root) {
            return String.valueOf(INF);
        }
        StringBuilder sb = new StringBuilder();
        sb.append(root.val)
        .append("_")
        .append(Serialize(root.left))
        .append("_")
        .append(Serialize(root.right));
        
        return sb.toString();
    }

    TreeNode Deserialize2(String str) {
        if (null == str || "".equals(str)) {
            return null;
        }
        //将节点元素值分离
        String[] s = str.split("_");
        List<String> list = Arrays.stream(s).collect(Collectors.toList());
        TreeNode root = buildTree(list);
        return root;
    }

    private TreeNode buildTree(List<String> list) {
        int rootValue = Integer.parseInt(list.remove(0));
        if ( rootValue == INF) {
            return null;
        }
        TreeNode root = new TreeNode(rootValue);
        root.left = buildTree(list);
        root.right = buildTree(list);
        return root;
    }
}