一、编程题：142. 环形链表 II（双指针-快慢指针）

1.题目描述

给定一个链表的头节点 head ，返回链表开始入环的第一个节点。如果链表无环，则返回 null。
如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。如果 pos 是 -1，则在该链表中没有环。注意：pos 不作为参数进行传递，仅仅是为了标识链表的实际情况。
不允许修改链表。 LeetCode题目链接。

2.示例1：

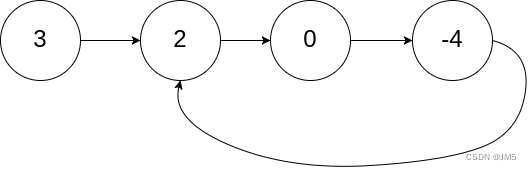
在这里插入图片描述

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。

3.示例2：

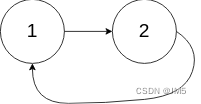
在这里插入图片描述

输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。

4.示例3：

在这里插入图片描述

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

5.提示：

链表中节点的数目范围是 [0, 104]
-10^5 <= Node.val <= 10^5
pos 为 -1 或者链表中的一个有效索引。

6.提示：

你能用 O(1)（即，常量）内存解决此问题吗？

二、解题思路

这题可采用快慢指针，其关键点还是该怎么去移动这两个指针？这一点要理清楚。慢指针针每次走一步，快指针每次走两步，如果相遇就说明有环，如果有一个为空说明没有环。然后在有环的基础上需要找出入环的第一个结点，这里就涉及到一些公式推导了。

1.思路

解决方法1（个人想法）：

快慢指针第一次相遇：

Step 1.创建快慢指针slow和fast，两者初始化均为 head，在运行过程中，slow每次向后走一步，fast每次向后走两步，如果slow==fast时，说明有环返回true;
Step 2.当循环正常结束时，说明链表中没有环，即返回false;

当快慢指针第一次相遇（fast==slow）时，可以分析此时fast和slow的移动步数关系：

设链表头结点到环入口的结点个数为a（不计链表入口结点），环内结点个数为b，则从头结点走到环入口结点就会有以下两种情况：
1、从结点直接走到环入口结点，需要a步即可;
2、从结点走到环中，然后从环中走到环入口结点（这里可以在环多走几圈），则需要a+k*b(1)（其中k为圈数，k大于等于0的整数值）步即可;
由上面两种情况可以把链表头结点到环入口所需要的步数归纳为a+k*b步（其中k为圈数，k大于等于0的整数值）
由于slow每次走一步，fast每次走两步，所以可得到DF=2*DS(2)；
当fast与slow相遇的时候，快慢指针都走过了a步，然后在环内绕圈直到相遇，此时fast比slow多走了n个环的长度，即DF=DS+n*b(3)；结合(2)(3)公式可得 2*DS=DS+n*b，化简得DS=n*b（其中n为圈数）;

（注：因为快慢指针之间存在速度差，且差值为1，当链表中存在环时，fast必然与slow相撞，可以画图理解一下）

快慢指针第二次相遇：

Step 1.将fast指针指向头结点，与slow进行移动直至相遇（此时fast每次只移动一步），相遇则返回该结点即可；

这里是解决问题的关键，根据之前第一次相遇的fast和slow的步数关系可知道链表头结点到环入口所需要的步数为a+k*b，DS=n*b，这里就可知道当slow指针再移动a步时，就能得到DS=a+n*b，刚好就到达了入口结点，证毕；
综上所述，只要当快慢指针第一次相遇后，只需要把slow再移动a步即可

2.复杂度分析：

时间复杂度: O(N)，最坏情况为O(N)+O(N)，因此总体为线性复杂度O(N)
空间复杂度: O(1)

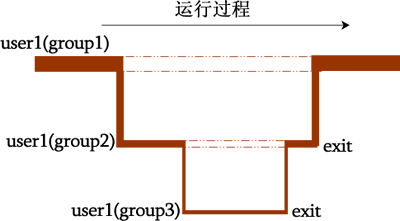
3.算法图解

红色部分代表快慢指针相撞。（注：本人不会做成流程动画，希望会的朋友可以私信我指点一二，说个软件名字也可以，谢谢）

第一次相遇：

请添加图片描述

第二次相遇：

请添加图片描述

三、代码实现

每个代码块都写了注释，方便理解，代码还可以改进；
(根据个人想法编写)

public class Solution {
    public ListNode detectCycle(ListNode head) {
        ListNode slow = head, fast = head;
        while(fast != null && fast.next != null){
            slow = slow.next;
            fast = fast.next.next;
            // 第一次相遇
            if(slow == fast){
                fast = head;
                while(true){
                    // 第二次相遇
                    if(slow == fast) return slow;
                    slow = slow.next;
                    fast = fast.next;
                }
            }
        }
        return null;
    }
}