1 行内公式
在两个美元符号中输入公式即可。
如$E=m\times c^2$ 效果:
E
=
m
×
c
2
E=m\times c^2
E=m×c2(注:\times是乘的意思)
2 整行公式
在四个美元符号中输入公式,如果想要给公式后面添加编号,那么在公式后添加空格 + \tag{1}就可以了。
如$$ \sum_{i=0}^n i^2=\frac{(n^2+n)(2n+1)}{6} \tag{1} $$,效果:
∑
i
=
0
n
i
2
=
(
n
2
+
n
)
(
2
n
+
1
)
6
(1)
\sum_{i=0}^n i^2=\frac{(n^2+n)(2n+1)}{6} \tag{1}
i=0∑ni2=6(n2+n)(2n+1)(1)
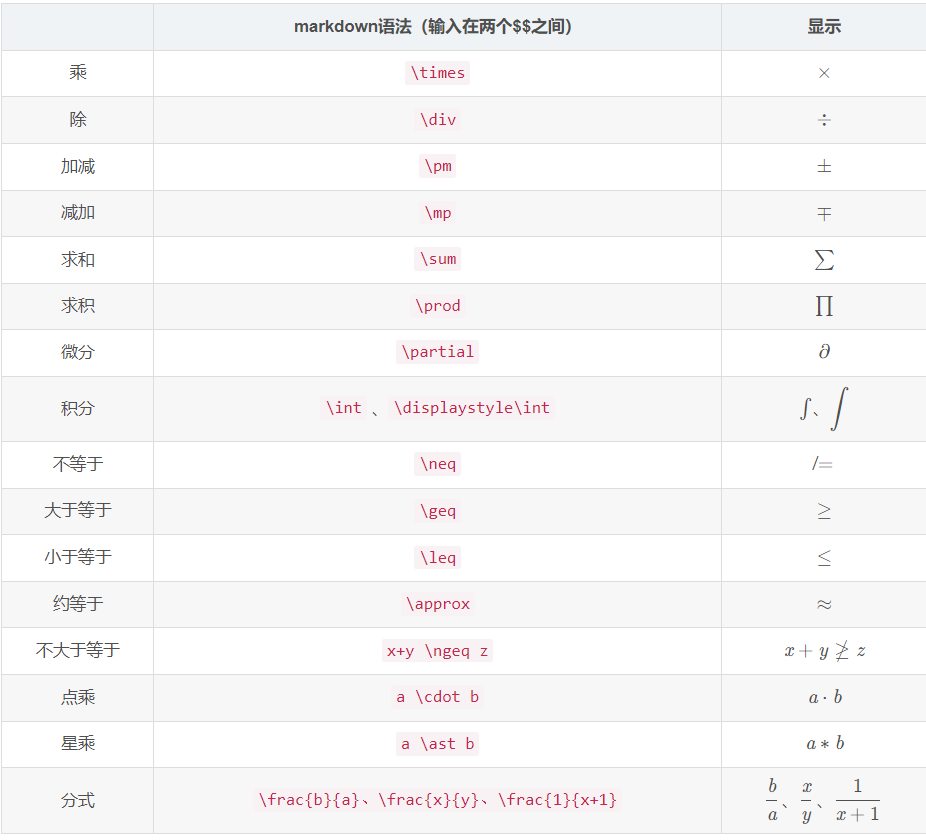
3 希腊字母


从上表可以看到,希腊字母的LaTeX公式都是希腊字母的英文名,小写希腊字母就是全小写的英文,大写希腊字母就是英文首字母大写。
4 上标与下标
用_表示下标,^表示上标。
如$$ x_i^3+y_i^3=z_i^3 \tag{2} $$,效果:
x
i
3
+
y
i
3
=
z
i
3
(2)
x_i^3+y_i^3=z_i^3 \tag{2}
xi3+yi3=zi3(2)
如$$ MSE=\sum_{i=1}^n (w\times x_i+b-y_i)^2 \tag{3} $$,效果:
M
S
E
=
∑
i
=
1
n
(
w
×
x
i
+
b
−
y
i
)
2
(3)
MSE=\sum_{i=1}^n (w\times x_i+b-y_i)^2 \tag{3}
MSE=i=1∑n(w×xi+b−yi)2(3)
5 括号
()和[] 可以直接输入,但花括号{ }前面需要加转义符号\。
如$$ \{[(x_1+x_2)^2-(y_1-y_2)^4]\times w\}\times (z_1^2-z_2^2) \tag{4} $$ ,效果:
{
[
(
x
1
+
x
2
)
2
−
(
y
1
−
y
2
)
4
]
×
w
}
×
(
z
1
2
−
z
2
2
)
(4)
\{[(x_1+x_2)^2-(y_1-y_2)^4]\times w\}\times (z_1^2-z_2^2) \tag{4}
{[(x1+x2)2−(y1−y2)4]×w}×(z12−z22)(4)
6 累加、累乘、并集和交集
累加:使用 \sum_{下标表达式}^{上标表达式} {累加表达式}
如$$ Y_i=\sum_{i=0}^{n} X_i \tag{5} $$,效果:
Y
i
=
∑
i
=
0
n
X
i
(5)
Y_i=\sum_{i=0}^{n} X_i \tag{5}
Yi=i=0∑nXi(5)
与累加类似,
累乘使用 $\prod$
并集使用 $\bigcup$
交集使用 $\bigcap$
例如:
$$ \sum_{i=1}^n \frac{1}{i^2} \quad and \quad \prod_{i=1}^n \frac{1}{i^2} \quad and \quad \bigcup_{i=1}^{2} \Bbb{R} \quad and \quad \bigcap_{i=1}^3 X_i \tag{6}$$
∑
i
=
1
n
1
i
2
a
n
d
∏
i
=
1
n
1
i
2
a
n
d
⋃
i
=
1
2
R
a
n
d
⋂
i
=
1
3
X
i
(6)
\sum_{i=1}^n \frac{1}{i^2} \quad and \quad \prod_{i=1}^n \frac{1}{i^2} \quad and \quad \bigcup_{i=1}^{2} \Bbb{R} \quad and \quad \bigcap_{i=1}^3 X_i \tag{6}
i=1∑ni21andi=1∏ni21andi=1⋃2Randi=1⋂3Xi(6)
7 对数
如$\log_2 10$,效果:
log
2
10
\log_2 10
log210
如$\lg 10^3$,效果:
lg
1
0
3
\lg 10^3
lg103
如$\ln (\pi+2)$,效果:
ln
(
π
+
2
)
\ln (\pi+2)
ln(π+2)

8 三角函数
如$$ \sin(x+y)+\cos(y+z)+\tan(z+x)+\arcsin(x+y+z) \tag{7}$$,效果:
(
x
+
y
)
+
cos
(
y
+
z
)
+
tan
(
z
+
x
)
+
arcsin
(
x
+
y
+
z
)
(7)
(x+y)+\cos(y+z)+\tan(z+x)+\arcsin(x+y+z) \tag{7}
(x+y)+cos(y+z)+tan(z+x)+arcsin(x+y+z)(7)
9 运算符
如$\frac{\partial f(x,y)}{x}$,效果:
∂
f
(
x
,
y
)
x
\frac{\partial f(x,y)}{x}
x∂f(x,y)
如$\int_a^{+\infty} x^2 dx,效果:
∫
a
+
∞
x
2
d
x
\int_a^{+\infty} x^2 dx
∫a+∞x2dx