一、解释器模式是什么？

解释器模式是一种行为型的软件设计模式，定义了一个解释器，来解释给定语言和文法的句子。也可以理解为翻译吧，比如1+1，翻译为一加上一，等于二，这样就做成了一个简单的加法计算器。

解释器模式的优点：

良好扩展性。语法的翻译通过类来实现，扩展类可以扩展其解释能力。
易实现。语法树中每个表达式节点类具备一定相似性，实现起来相对容易。

解释器模式的缺点：

执行效率低。解释器中通常有大量循环和递归语句，当被解释句子较复杂时，程序的性能受到较大影响。
类膨胀。规则较多时，类数量也膨胀。

二、解释器模式

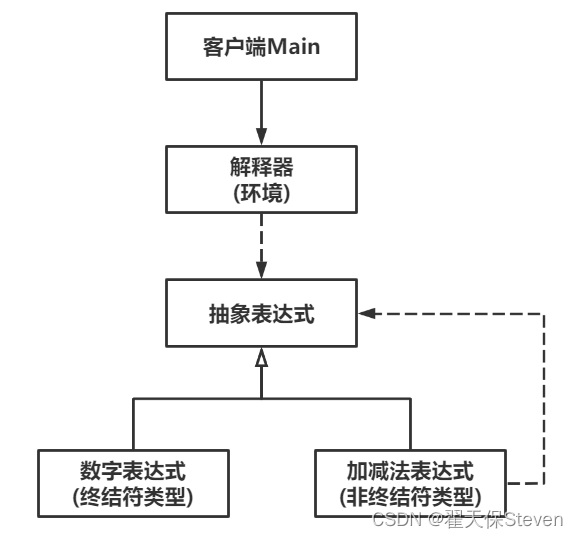
2.1 结构图

客户端即Main主函数，客户端通过解释器来解析表达式内容，表达式又分为终结型和非终结型。就拿计算器举例，1+1,1就是终结符类型，表达式可以用它结尾；而+就是非终结符类型，出现了+，就意味着它前后还有别的表达式字符，自然不能作终结。

2.2 代码示例

场景描述：实现简单的加减法计算器。

//Interpreter.h
/****************************************************/
#pragma once
#include <iostream>
#include <vector>
#include <string>
#include <algorithm>
#include <stack>

using namespace std;

// 抽象表达式类
class Expression 
{
public:
	// 解释
	virtual int interpret() = 0;

};

// 数字表达式类
class NumberExpression : public Expression 
{
public:
	// 构造函数
	NumberExpression(int num) : number(num) {}

	// 解释
	virtual int interpret() { return number; }

private:
	int number;
};

// 加法表达式类
class AddExpression : public Expression 
{
public:
	// 构造函数
	AddExpression(Expression* left, Expression* right) : left(left), right(right) {}

	// 解释
	virtual int interpret() { return left->interpret() + right->interpret(); }

private:
	Expression* left;
	Expression* right;
};

// 减法表达式类
class SubExpression : public Expression 
{
public:
	// 构造函数
	SubExpression(Expression* left, Expression* right) : left(left), right(right) {}

	// 解释
	virtual int interpret() { return left->interpret() - right->interpret(); }

private:
	Expression* left;
	Expression* right;
};

// 解释器类
class Interpreter 
{
public:
	// 构造函数
	Interpreter(string exp) : expression(exp) {}

	// 解释
	int interpret() {
		stack<Expression*> s;
		// 遍历表达式字符
		for (int i = 0; i < expression.length(); i++) {
			if (isdigit(expression[i])) {
				// 识别数字
				int j = i;
				while (j < expression.length() && isdigit(expression[j])) {
					j++;
				}
				int num = stoi(expression.substr(i, j - i));
				s.push(new NumberExpression(num));
				i = j - 1;
			}
			else if (expression[i] == '+') {
				// 把左数提取出来
				Expression* left = s.top();
				s.pop();
				// 识别右数
				int j = i + 1;
				while (j < expression.length() && isdigit(expression[j])) {
					j++;
				}
				Expression* right = new NumberExpression(stoi(expression.substr(i + 1, j - (i + 1))));
				// 左数+右数的表达式放入栈中
				s.push(new AddExpression(left, right));
				i = j - 1;
			}
			else if (expression[i] == '-') {
				// 把左数提取出来
				Expression* left = s.top();
				s.pop();
				// 识别右数
				int j = i + 1;
				while (j < expression.length() && isdigit(expression[j])) {
					j++;
				}
				Expression* right = new NumberExpression(stoi(expression.substr(i + 1, j - (i + 1))));
				// 左数-右数的表达式放入栈中
				s.push(new SubExpression(left, right));
				i = j - 1;
			}
		}
		return s.top()->interpret();
	}

private:
	string expression;
};

//main.cpp
/****************************************************/
#include <iostream>
#include <string>
#include <unordered_map>
#include "Interpreter.h"

using namespace std;

int main() 
{
	unordered_map<string, int> variables;
	string input;
	while (getline(cin, input)) {
		cout << "input:" << input << endl;
		Interpreter interpreter(input);
		variables[input] = interpreter.interpret();
		cout << "result:" << variables[input] << endl;
	}

	return 0;
}

程序结果如下。