【计算机组成原理】数据的表示和运算·进位计数制

news2025/1/9 1:33:44

🚩 本文已收录至专栏：计算机基础

我们可以通过显示屏看到各种形式的数据信息，但数据是如何在计算机中表示呢？运算器又是如何实现数据的算数、逻辑运算？

十进制数是最适合我们日常使用的一种计数方式，除此之外，我们还会用到八进制数和十六进制数，但二进制是最适合计算机使用的计数方法，这是因为：

它可以使用两个稳定状态的物理器件来进行表示，例如高低电压。
0，1正好对应逻辑值假、真。方便实现逻辑运算。
可以很方便地使用逻辑门电路实现算数运算。

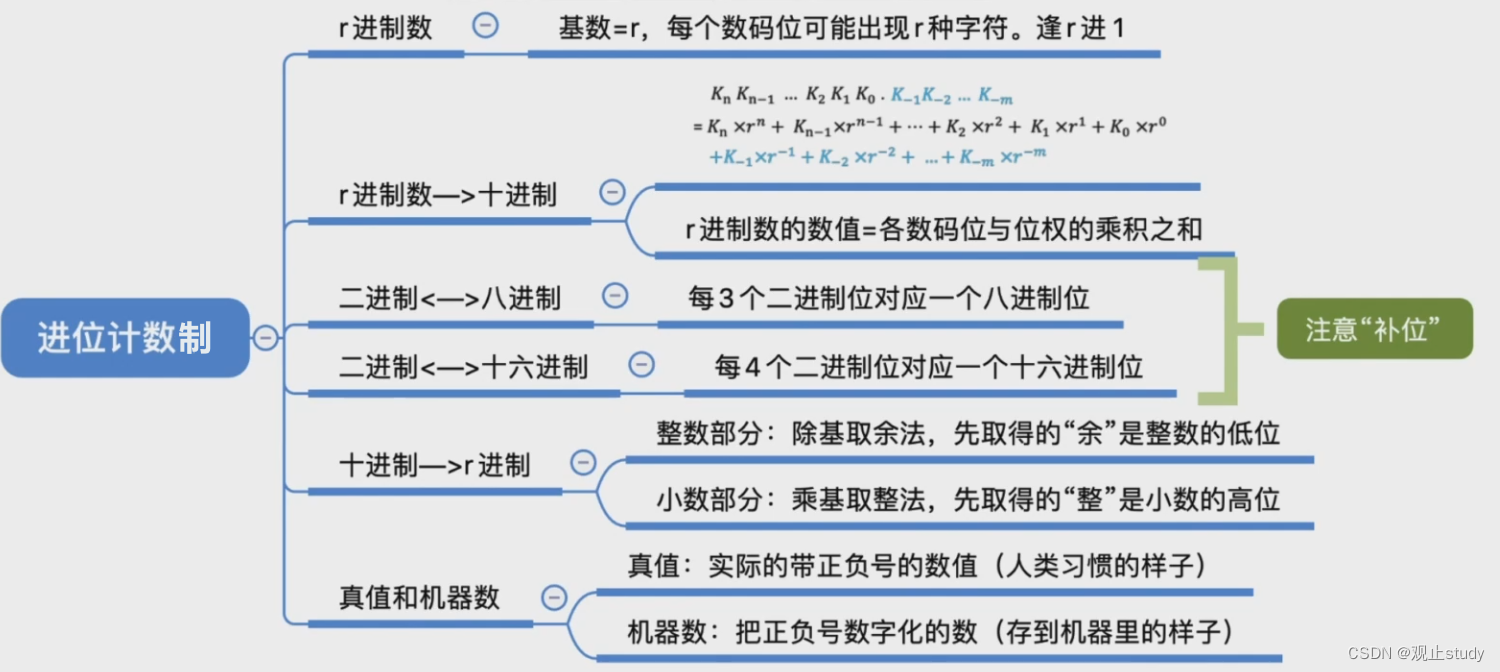
文章内容概览：
在这里插入图片描述

一.演变历程

我们的计数形式进行了长期的演变，尽管象征计数意义的符号在不断的发生改变，淘汰一套又一套，但其核心思想使用不同的符号代表不同权重却始终未曾发生改变，只是为了适应多变与复杂的情景在不断的进行改进，使其使用更加便利。

例如我们先使用‘ I ’代表 1个，物品增多后发现 I 太多了不方便，便引入‘ 一 ’代表 5个 ,以此简化表示。
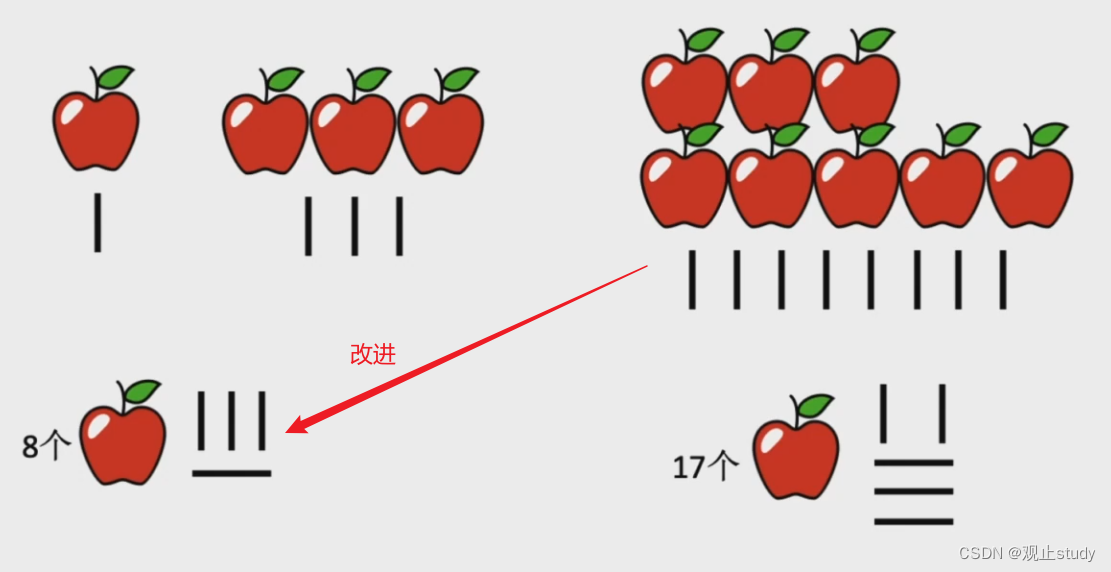
随着时间的推移，计数越来越庞大，为了便捷我们便又引入了更多的符号代表不同的权值。由于这种方式是基于“ 加法 ”思想的计数方法，随着数据规模增大，相应表示也不可避免的会越来越复杂。例如：DMCLXVI -> 1000+500+100+50+10+5+1 = 1666
为了解决上述问题，我们又发明了基于“ 乘法 ”思想的计数方法，仍旧是使用不同符合代表权重，但是不再是一个固定值，而是根据所在位置动态变化,也就是说符号所在的位置也反应权重。由此催生了我们现在最常使用的十进制数。符号权值 = 符号值 × 符号所处位置权值。
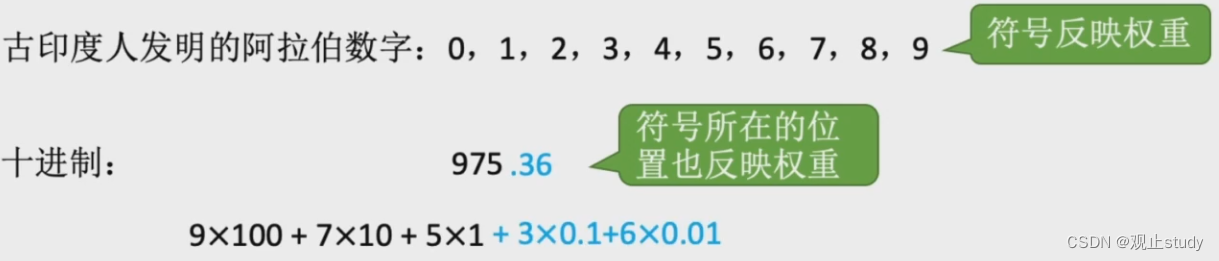
由此我们可以推断出其表达公式：
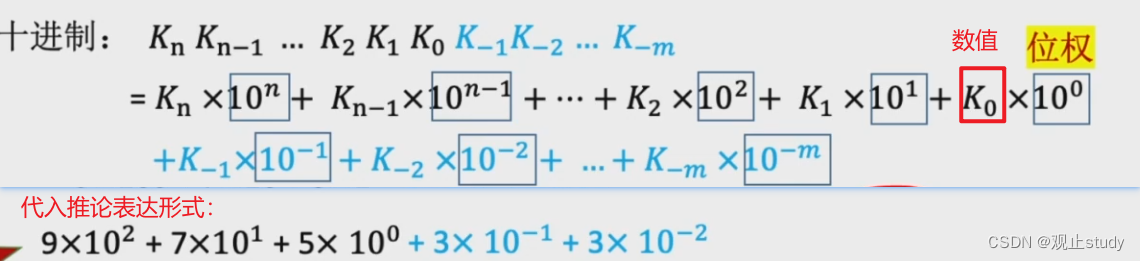
由于 0~9 一共只有十种符号，要表达加法的时候必须逢十进一，这也是为什么叫做十进制。

二.进位计数制

(1) 引入

基于“ 乘法 ”思想的计数方法，我们可以根据权值符号的数量不同得出不同的进制计数法。

我们使用基数表示每个数码位所用到的不同符号的个数，r 进制的基数为 r。例如：十进制表示每个位置可以用到十种不同的符号。

由此可以得出二进制，八进制，十进制，十六进制：

二进制：0，1 ====> 每个位置两种表示符号

八进制：0，1，2，3，4，5，6，7 ====> 每个位置八种表示符号

十进制：0，1，2，3，4，5，6，7，8，9 ====> 每个位置十种表示符号

十六进制：0，1，2，3，4，5，6，7，8，9，A，B，C，D，E，F ====> 每个位置十六种表示符号

其加法运算方式与十进制类似，同样是逢 r 进一。例如：

二进制： 11 + 11 = 110 逢二进一

运算：0号位：1 + 1 = 2 = 2(进位) + 0 1号位：1 + 1 + 1(进的一) = 3 = 2(进位) + 1 2号位： 1(进的一)

八进制： 54 + 55 = 131 逢八进一

运算： 0号位：4 + 5 = 9 = 8(进位) + 1 1号位：5 + 5 + 1(进的一) = 11 = 8(进位) + 3 2号位：1(进的一)

十进制： 37 + 55 = 92 逢十进一

运算： 0号位：5 + 7 = 12 = 10(进一) + 2 1号位：5 + 3 + 1(进的一) = 9

十六进制：59 + 58 = B1 逢十六进一

运算： 0号位：8 + 9 = 17 = 16(进一) + 1 1号位：5 + 5 + 1(进的一) = 11 = B

注意：十六进制中 A -> 10 B -> 11 C -> 12 D -> 13 E -> 14 F -> 15

(2) 任意进制 <-> 十进制

(2.1) 任意进制 -> 十进制

我们可以得出任意进制转 r 进制公式，得到一套快速计算任意进制转为十进制的计算模板。记小数点左边第一位为0号位置:

十进制 = Σ(数码位值× 基数 ^ 位置) = Σ(数码位值× 位权)
在这里插入图片描述

(2.2) 十进制-> 任意进制

对于十进制转为其他任意进制我们也有一套通用的计算模板，但是对于整数部分和小数部分的计算方式却有所差异。

对于整数部分：r进制整数部分 = （十进制整数部分 % r）不断取余数

例如：我们将十进制 75 转为二进制数，最后结果为：1001011，注意顺序！
在这里插入图片描述

十进制转为其他进制写法类似：
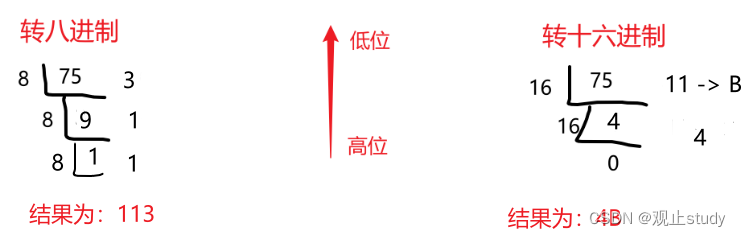
在这里插入图片描述

对于小数部分：r进制小数部分 = （十进制小数部分 × r ）不断取出整数

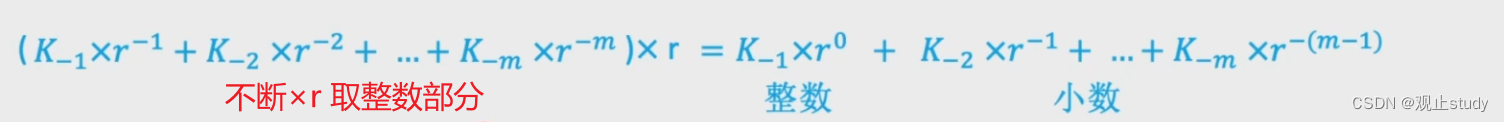
例如：我们将十进制 0.3 转为二进制数，最后结果为：0.01001…可以发现无限循环了，也就是说我们无法获取到其二进制的精确表示，于此对于无限小数我们只需取到指定精度即可，注意顺序！
在这里插入图片描述
十进制转为其他进制写法类似：

(3) 二进制 <-> 八进制

(3.1) 二进制 -> 八进制

我们知道八进制的基数为 8，即每个位数可以表示八种不同情况。而二进制的基数为 2，即每个位数可以表示两种不同情况。假如我们把三个二进制位组合便可以得到2×2×2=8种不同情况，正好对应八进制每个数码位的八种情况。由此，我们可以得出二进制转八进制的计算方式：将二进制数每3位分为一组，每组转换成对应的八进制符号。
在这里插入图片描述

由此上述二进制 -> 八进制为：1111000010.011010 -> 1702.32

注意：当小数点左边位数不够3的整数倍向左补0，当小数点右边位数不够3的整数倍向右补0。

(3.2) 八进制 -> 二进制

八进制转为二进制相当于一个逆向的过程，即每位八进制数可以对应 3 位二进制数。我们只需一一将每位八进制数转为二进制形式即可获取到其所对应的二进制数。
在这里插入图片描述

例如上述我们将八进制数251.5转为二进制数，只需一一转为二进制数再进行组合即可。

(4) 二进制 <-> 十六进制

(4.1) 二进制 -> 十六进制

同理，我们知道十六进制的基数为16，即每个位数可以表示十六种不同情况。而二进制的基数为2，即每个位数可以表示两种不同情况。假如我们把四个二进制位组合便可以得到2×2×2×2=16种不同情况，正好对应十六进制每个数码位的十六种情况。由此，我们可以得出二进制转十六进制的计算方式：将二进制数每4位分为一组，每组转换成对应的十六进制符号。
在这里插入图片描述