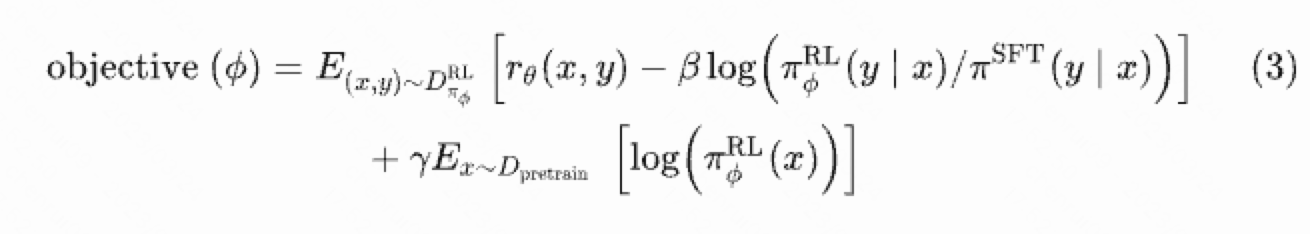决策树作为一个分类问题，以信息增益作为特征分类的参考依据，作为一个分类算法，决策树可以将分类过程可视化，而且对于模型所不熟悉的数据，决策树也可以从中提炼出一系列的规则，然后根据数据来创造规则，决策树的优点：易于理解，可以处理不相关的数据等等。其缺点也很明显：可以会过拟合。

        决策树的伪代码很通俗易懂，是一个递归的模型：首先如果只有一个特征的时候，那么就跳出递归，如果有多个特征，首先从多个特征中选取划分数据集最好的特征，然后对数据集进行划分，建立分支的节点，然后对每一个分支再进行递归，直至终止。

        信息增益作为决策树划分数据集的重要依据之一，它的意义是使无序的数据变得更有序，在理解信息增益之前，需要了解熵：熵可以理解为信息的期望值，信息的公式记作,其中为选择该分类的概率。所以熵的公式为：

        代码如下

def calculateentropy(dataset):
    len_entropy =len(dataset)
    label={}
    for featurevect in dataset:
        feature=featurevect[-1]
        if feature not in label.keys():
            label[feature]=0
        label[feature] +=1
    entropy=0.0
    for key in label.keys():
        proba =float(label[key])/len_entropy
        entropy += -proba*log(proba,2)
    return entropy
        

        这里的第一个循环时统计各个特征值的个数，这样子方便得到概率。下面以一个简单的数据进行测试。

def createDataset():
    dataset =[[1,1,'yes'],
             [1,1,'yes'],
             [1,0,'no'],
             [0,1,'no'],
             [0,1,'no']]
    labels=['no surfacing','flippers']
    return dataset ,labels
calculateentropy(dataset)

        在计算完熵之后，我们就可以通过最大的信息增益的方法来划分数据集。

def splitDataset(dataset,axis,value):
    reducedset=[]
    for featurevect in dataset:
        if featurevect[axis] ==value:
            reducedfeaturevect =featurevect[:axis]
            reducedfeaturevect.extend(featurevect[axis+1:])
            reducedset.append(reducedfeaturevect)
    return reducedset

         其中的参数axis为特征，value为期待的值。最后我们将两个代码进行整合，得到最终的代码。

def choosebestfeaturetosplit(dataset):
    num_feature=len(dataset[0])-1
    baseentropy =calculateentropy(dataset)
    bestinfogain=0.0
    bestfeature=-1
    for feature in range(num_feature):
        featurelist =[example[feature] for example in dataset]
        featureset =set(featurelist)
        featureentropy=0.0
        for value in featureset:
            subdataset =splitDataset(dataset,feature,value)
            proba =len(subdataset)/float(len(dataset))
            featureentropy += proba*calculateentropy(subdataset)
        infogain =baseentropy -featureentropy
        print(feature,infogain)
        if infogain >bestinfogain:
            bestinfogain =infogain
            bestfeature =feature
    return bestfeature
        

        在建立好决策树的代码之后，为了让内部过程可视化，我们建立了一个建立树的代码。

def createtree(dataset,labels):
    classlist =[example[-1] for example in dataset]
    if classlist.count(classlist[0]) ==len(classlist):
        return classlist[0]
    if len(dataset[0])==1:
        return majoritycnt(classlist)
    bestfeature =choosebestfeaturetosplit(dataset)
    print(bestfeature)
    bestfeaturelabel =labels[bestfeature]
    mytree ={bestfeature:{}}
    del(labels[bestfeature])
    featurevalues =[example[bestfeature] for example in dataset]
    uniqueval = set(featurevalues)
    for value in uniqueval:
        sublabels =labels[:]
        mytree[bestfeaturelabel][value]=createtree(splitDataset(dataset,bestfeature,value),sublabels)
    return mytree

        在这里我们需要建立另外一个函数，作为决策树的分类函数，他作为一个递归函数，会对整个树进行遍历，然后找到数据该存储的位置以及特征的选择。

import operator
def majoritycnt(classlist):
    classCount={}
    for vote in classlist:
        if vote not in classCount.keys():
            classCount[vote]=0
            classCount[vote]+=1
    sortedclasscount =sorted(classCount.items(),key =operator.itemgetter(1),reverse =True)
    return sortedclasscount[0][0]    

         最后，我们以用决策树来预测隐形眼镜类型来收尾。

        

fr =open('lenses.txt')
lenses=[inst.strip().split('\t') for inst in fr.readlines()]
lenseslabels=['age','prescript','astigmatic','tearRate']
lensestree=createTree(lenses,lenseslabels)
lensestree