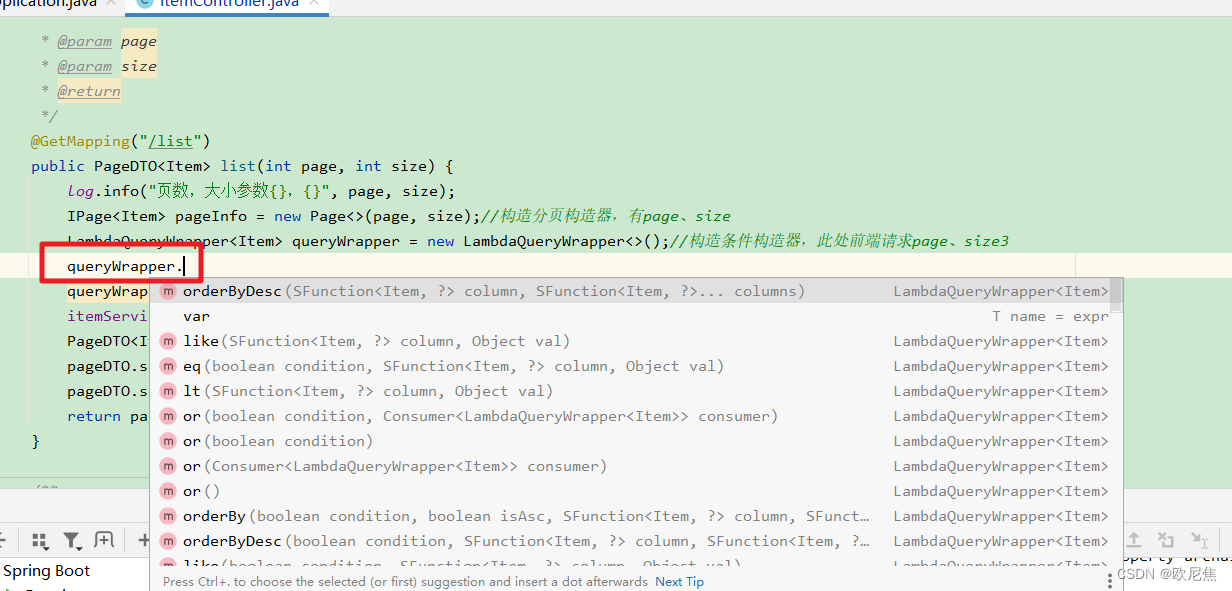
目录
一、电感的种类
1、共模电感
2、差模电感
3、工字电感 功率电感
4、磁珠
5、变压器
6、R棒电感、棒形电感、差模电感
二、电感符号
三、电感特性
前面在学习电容的时候,为了让大家更形象,更通俗的去理解这个元器件,都是拿水缸去打比方的,但是对于电感,我们很难拿生活中的例子去类比
一、电感的种类
电感的种类有很多种,比如共模电感,差摸电感,功率电感,滤波电感,贴片电感等等。
甚至变压器也可以看成是一个电感,电机也是一种电感,把线圈一圈一圈的绕制在一个磁芯上,就构成了电感
1、共模电感
下面的照片,中间绕一个圆环形的磁芯,外面绕了一匝一匝的线圈,再引出4个脚,这样的电感基本都是共模电感。这个电感的作用就是抑制共模干扰的。
但是由于制造的工艺不同,它不光有磁芯,还有塑料骨架,由于有骨架,它明显容易固定一些,引线也不容易断
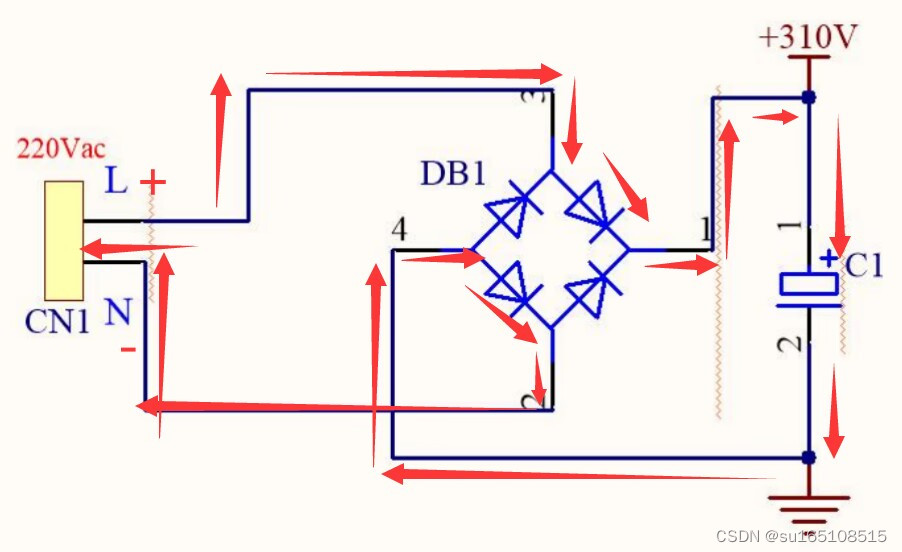
下图是一个桥式整流电路,一个整流桥+电容,就可以把一个220V的交流电,整流成310V的直流电
在这个电路中:当L电压高于N电压的时候,电容C1上的电流是从上流到下
当N电压高于L电压的时候,电容C1上的电流还是从电容上端流到电容下端
所以,不管是L电压高于N电压,还是N电压高于L电压,对于电容来说,电流始终从电容C1的上端流向电容的下端,也就是说,L和N之间是交流电,而电容C1上端的电压始终高于下端电压,C1两端的电压方向是不变的。
而且,电容C1起到了储能的作用,后级负载需要电能,电容C1就供给后级,如果我们把电容C1两端的电压变化控制在一个范围内,我们就认为电容C1两端电压近似不变
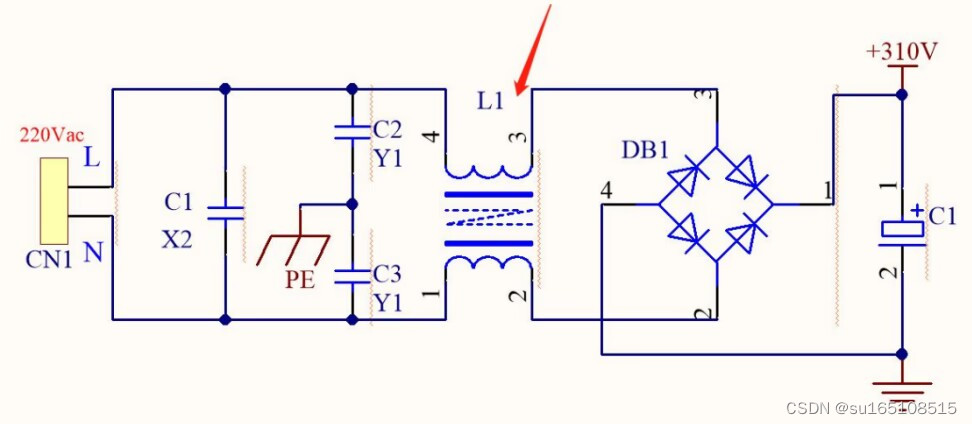
下图的L1就是共模电感,这个电感的作用就是抑制共模干扰的
C1是X电容,抑制的是差摸干扰,共模电感抑制的是共模干扰
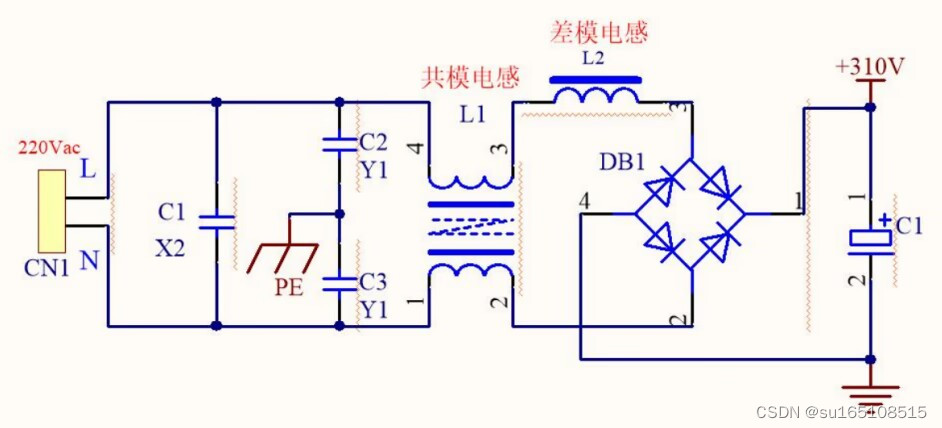
2、差模电感
下面的是差摸电感,大家可以看到它有两个引脚
差摸电感在交流转直流电路中是用来抑制差摸干扰的

3、工字电感 功率电感
这是另外一种电感,我们一般叫它功率电感或者工字电感
在后面要学习的BUCK电路中,会使用这样的电感
插件工字电感/功率电感 贴片工字电感/功率电感


不管是插件的工字电感,还是贴片的工字电感,它的外围都是有很强的干扰的
是因为,它所处的工作环境就是高频场合,会存在很多干扰。
所以,就有了这种一体成型的电感,这种电感一般用在BUCK电路中,外围的金属可以起到很好的干扰屏蔽作用。

4、磁珠
这样的电感,外形和贴片电容差不多,这种电感叫做:磁珠
它是用来滤除信号级别的干扰的,比如通信口的干扰。
磁珠用于高频的场景,磁珠标注的一般是100MHz的阻抗值。

5、变压器
变压器的里面也有绕组线圈,也有磁芯

6、R棒电感、棒形电感、差模电感
这是R棒电感,也叫做差模电感,用在AC-DC电路中。
这种电感在安装尺寸上更有优势,占地面积更小。

二、电感符号
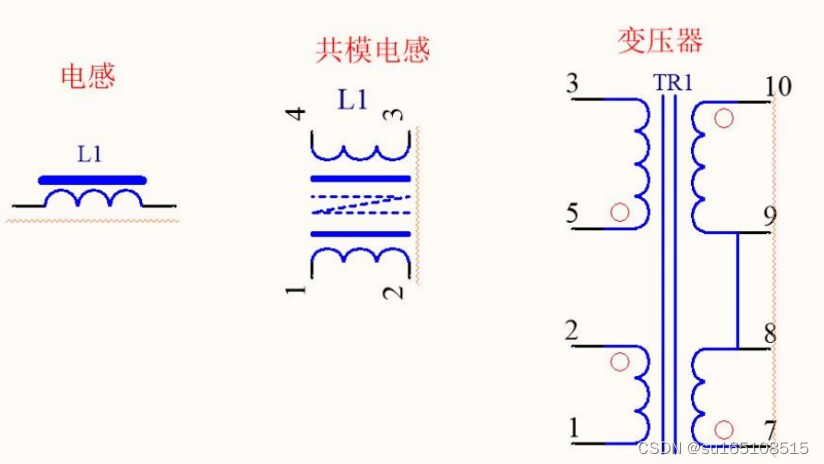
电感,共模电感,变压器,它们的原理图符号是有区别的
我们用这样的原理图符号来表示电感
电感 共模电感 变压器符号
三、电感特性
因为电感不仅涉及到电能,还涉及到了磁能,所以电感本身比较复杂,我们只能尽可能通俗的带大家认识电感,以实用为主,从实用的角度来认识电感。
前面我们在学习电容的时候,知道电容的特性是:通交隔直,电感也具有类似的性质,但是电感是反过来的,电感的特性是:通直阻交。
电容通高频阻低频,因为容抗Xc = 1/(2πfC),其中f是电源的频率,C是电容的容值,频率f越高,容抗越小,所以说,电容通高频阻低频,高频信号的时候,电容的容抗小,低频信号的时候,电容的容抗大。
而电感的感抗XL = 2πfL,其中f是电源的频率,L是电感的感量,当频率f大的时候,感抗就大,当频率f小的时候,感抗就小。所以对于高频信号来说,电感对高频信号的阻碍作用大,所以,电感是通低频,阻高频的。
我们知道,电容的本质就是充放电,对吧,不管是储能,还是滤波,都可以用充放电去理解。
而电感的感抗单位是Ω,很明显,电感也是阻碍电流的,但是这里要注意,严格的说,电感是阻碍电流的变化,而不是阻碍电流,电路中的电流想要变大,那么电感就阻碍电流变大,电路中的电流想要变小,那么电感就阻碍电流变小,反正,不管电流是变大还是变小,电感总是阻碍电流变化,而且,理想的电感不消耗任何能量,所以,电感可以用来储能,正是由于电感阻碍电流的变化,所以电感也可以用来滤波,
四、电感的能量公式
电感的能量公式是:E = 1/2*L*I²,其中L是电感的感量,I是流过电感的电流。
对于电容来说,电容两端的电压u和流过电容的电流i的关系是:I = C*du/dt。
那么,对于电感来说,也有一个类似的公式:U = L*di/dt。其中L表示电感的感量,di表示流过电感的电流的变化量,dt表示电流变化di所花费的时间,di/dt表示的是电流的变化速度。请问大家,我现在跑步,10秒钟跑了100米,那100米/10秒表示什么啊?是速度。
电感中的电流在dt=2秒内从10A增大到20A,那电流变化量di=(20A-10A),请问,di/dt=(20A-10A)/2是什么? 是不是在2秒时间内,电流的变化速度。
那么,对于电感来说,U = L*di/dt表示的是什么意思啊,电感两端的电压U和什么有关系?
电感两端的电压U正比于电感的电感量L,也正比于电感中电流的变化速度di/dt,对不对,也就是说电感中的电流变化速度越快,电感两端的电压就越高
那么,请问大家,同一个电感,当电感中的电流=100A的时候,电感两端的电压U等于多少?
电感中电流恒定等于100A的时候,电感两端感应的电压U就等于0,因为电流变化速度等于0,对不对,要注意区分电流的大小和电流的变化速度,电流变化速度等于0, U = L*di/dt中di/dt=0。
五、电感三个公式
感抗XL = 2πfL
电感中的能量E = 1/2*L*I²
电感两端电压和电感电流的关系:U = L*di/dt
六、电磁感应的基本知识
电容是以电场的方式来存储能量的,而电感之所以难以理解,是因为电感多了一个维度,
电感是以磁场的方式来存储能量的。
我们知道,电是会产生磁的,有电流流过,就会产生磁场。
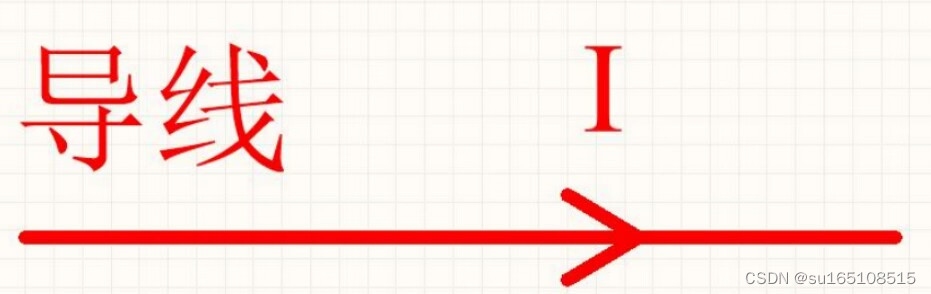
我们看上面这幅图,这根导线上流过电流I,根据电磁感应定律,在它周围会产生磁场。
磁场的方向是什么样子的?是根据右手螺旋定则来判断的,
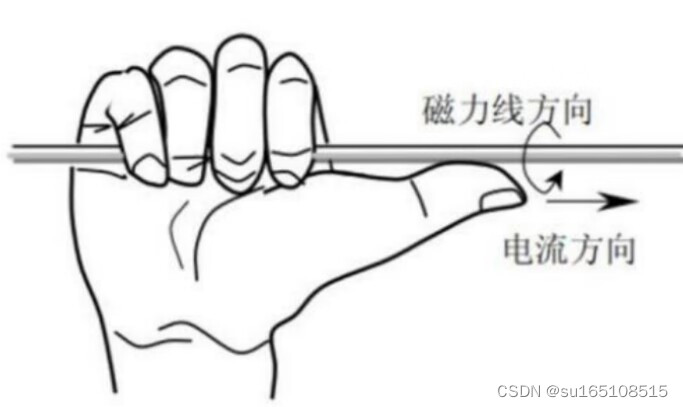
伸出右手,拇指指向电流方向,四指就是磁力线方向
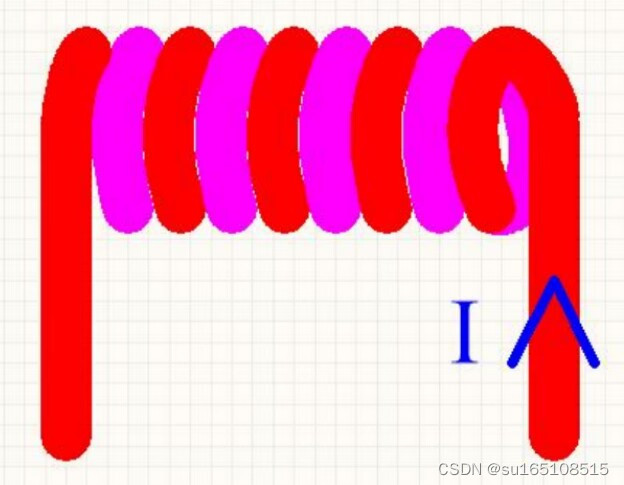
我们看上面的线圈,将导线绕成一圈一圈的,就成了线圈。
这个线圈中通入电流以后,同样会产生磁场,请问这个磁场的方向是什么样子的啊。
也是用右手螺旋定则判断,四指指向电流方向,拇指方向就是磁力线的方向。
但是,如果把导线绕成一圈一圈的话,线圈里面如果是空气的话,这个线圈电感的感量是很小的。
在实际工作中,几乎没有见过这样的产品。
如果在这样的电感线圈中间加一个磁芯的话,这个电感的感量就很大了,这是由于磁芯的磁导率比空气的磁导率大很多,它们之间相差很大很大,而电感量的大小,是和这个磁导率是有关系的,如果其他条件相同,一个是空心线圈,另一个是有磁芯的线圈,它们的感量L相差好几千倍,所以,带有磁芯的电感更具有实际应用价值。
七、感量和磁导率简单了解
我们知道,电容是以电场的方式存储能量的,这个电场的元素就是正负电荷,也就是电荷量Q,电容C的大小和电荷量Q,以及电压U之间存在这样的关系:Q = C*U。
而电感是以磁场的方式存储能量的,这个磁场中有一个元素就是磁链Ψ
电感L的大小,磁链Ψ,以及电流I之间的关系为:Ψ = L*I。磁链就是很多个线圈的磁通量。
单根线圈的磁通量用Ф来表示,N根线圈的磁通量用Ψ来表示,Ψ=N*Ф。磁通量Ф表示穿过某个截面的磁力线的条数,磁通 Ф=BA,B是磁感应强度,A 是电感的有效截面积,所以,磁链Ψ就等于Ψ = N*B*A。
磁动势用F来表示,F = I*N,也就是磁动势等于电流I和电感的匝数N的乘积。 磁动势在磁场哪个维度也有一个公式,就是:F = H*l 磁动势F=磁场强度H*磁力线的路径长度l I*N = H*l
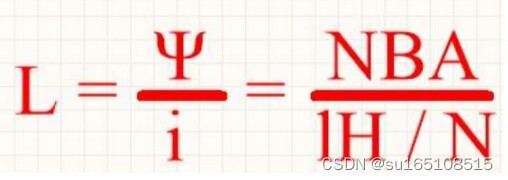
所以,就有了这么一个公式
而磁场强度H和磁感应强度B,它们之间也具有一个关系式:B = H* μ μ 就是磁导率
所以,我们得到了这个公式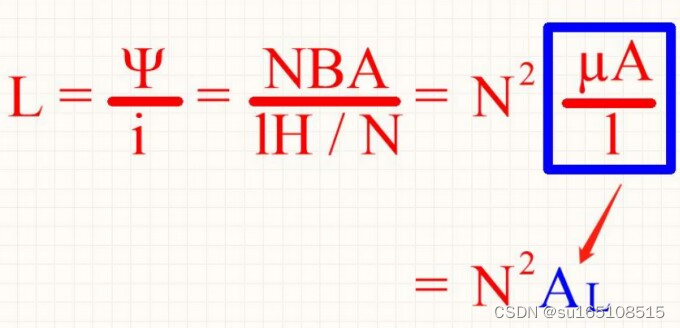
蓝框内的部分有一个统称,叫做电感系数,也可以写成AL,当一个电感的形状、尺寸、磁芯材质确定好了以后,那么电感系数AL也就确定了。
以上讲解的公式,只是让大家做一些了解,是不做要求的。
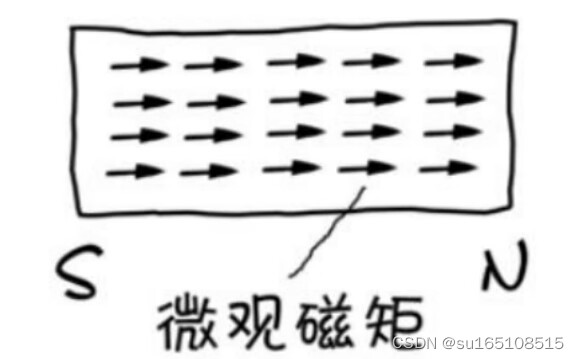
磁铁内部,在磁铁的内部,很多个电子绕着原子核旋转,电子绕着原子核旋转,它就会产生磁场,如上图中箭头表示的就是分子中电子旋转产生的磁场。产生的这个磁场可以看做是磁畴,无数个这样的磁畴,如果他们的方向趋于一致,宏观上就会产生磁场,就形成了磁铁。所以,从这个角度来说,磁铁也就是电生磁了,上图表示,当无数个磁畴的角度一致的时候,整个磁铁就对外表现出磁性,S表示磁铁的南极,N表示磁铁的北极。
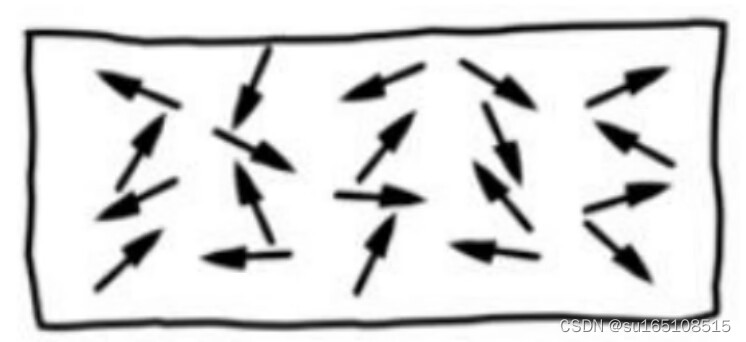
而当磁铁内部的磁畴是这样散乱的分布的时候,从宏观上来说,磁铁就没有磁性了。
如果在一个闭合导线周围,放一块磁铁,请问回路中会有电流产生吗? 这里的关键点就是:看闭合线圈所围的闭合区域中,区域中的磁场是否在变化,如果磁铁静止不动,其实对回路没有任何影响,只是在一个闭合导线周围放一块磁铁的话,磁铁不和导线产生相对运动的话,回路中是没有电流的,因为回路中的磁通量没有发生变化‘,如果这个磁铁是运动的,回路中就会产生电流,相应的也会有感应电动势,其实,这就是法拉第电磁感应原理了,其实关键就是看闭合回路中的磁通量有没有发生变化,只不过当时法拉第并没有把感应电动势的方向给定义出来,后来楞次就优化了一下,也就是楞次定律。
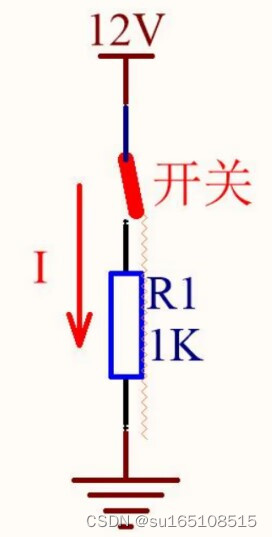
我们看上面这幅图,这是一个完整的源、回路、阻抗,当开关闭合时,回路中的电流是12mA。
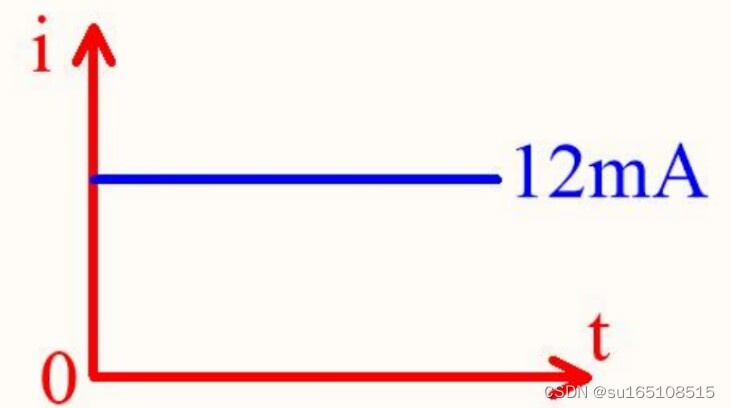
如果要画出波形,应该是这样子的。
我们设定在0时刻,就是开关闭合的时刻,当开关一闭合后,回路中的电流就从0mA瞬间变成了12mA,12mA就是这个回路所能达到的最大电流,因为有电阻R1把电流给限制住了。
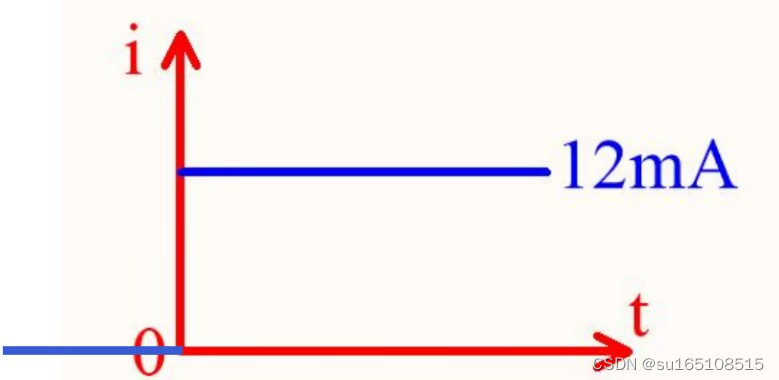
注意,蓝线表示的是回路中的电流,在0时刻,电流从0跳变为12mA。现在我们把电路修改以下,增加一个电感来看看
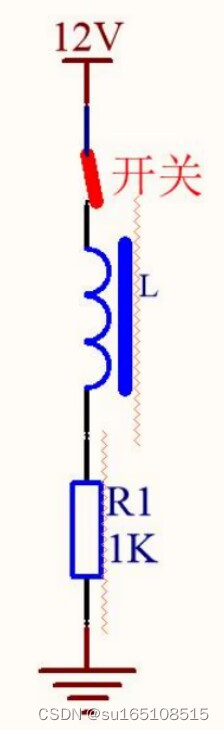
此时我们在回路中加了一个电感,此时当开关一闭合时,回路中的电流不是一下子就达到12mA的,这和刚才只有一颗电阻时是不同的,这是因为电感具有这么一个特性:电感具有阻碍电流变化的能力,注意啊,这里更深了一个层次,是阻碍电流变化,而不是阻碍电流。
当回路中的电流增大的时候,电感就阻碍电流变大,电感不让电流变大
当回路中的电流减小的时候,电流就阻碍电流变小,电感不让电流变小,换言之,电感中的电流不能突变,也就是说,电感中的电流只能连续变化。
我们把刚才两个电路中的电流变化画出来
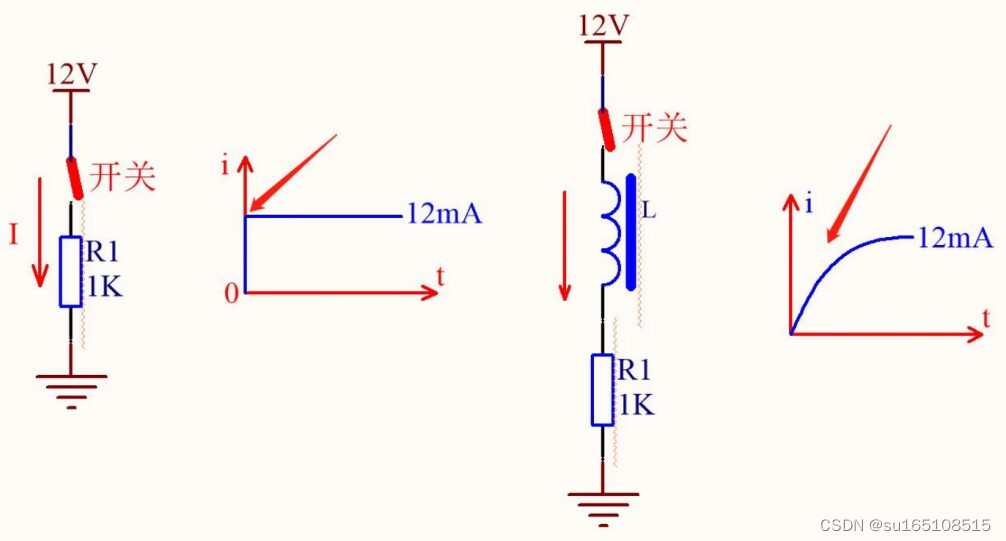
左图中,电阻上的电流是可以突变的,在t=0时从0跳变到12mA。
右图中,回路中的电流不是一下子就能达到12mA的,而是有一个缓慢连续变大的过程。
电感是具有自感电动势的,那么,在刚才的电路中,如何用自感电动势去分析呢
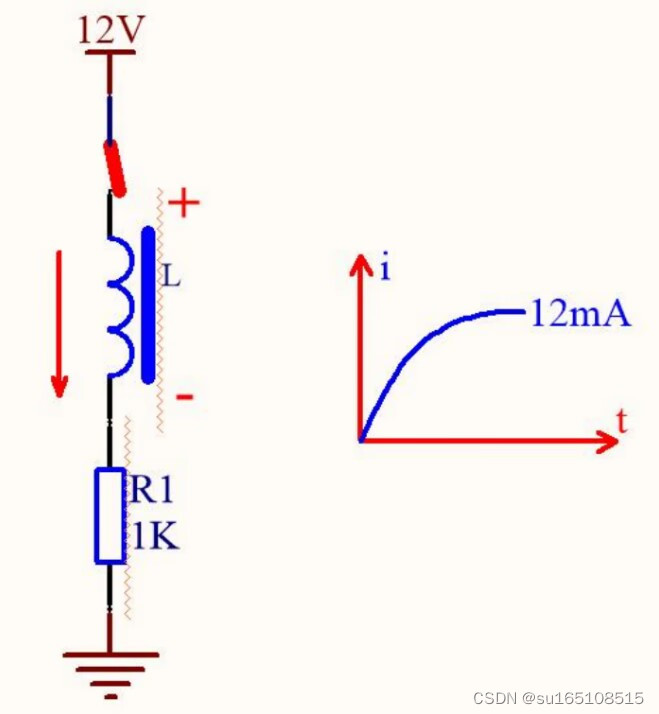
我们看上面这幅图,大家看到电感两端的+ -了没,在电路中,电感的自感电动势就是这么去标注的,我标的 + -,就是电感的自感电动势的方向,电感的自感电动势有一个公式:U = L*di/dt,电感中的电流i发生变化时,电感中的磁通量就随着电流变化了,变化的磁通量就会在电感两端感应出自感电动势U。
我们看,在开关刚刚闭合的一瞬间,由于电感中的电流不能突变,所以此时回路中的电流是多少?是0。开关刚刚闭合的瞬间,回路中的电流为0,要知道,此时电感的自感电动势就是12V,而且自感电动势和电源电压是反着的,所以,自感电动势和电源电压相互抵消了,回路中的电流才等于0
我们将这个公式整理一下
就得到了这个公式
等式左边就是电感上的电流变化率,也就是电流变化的快慢程度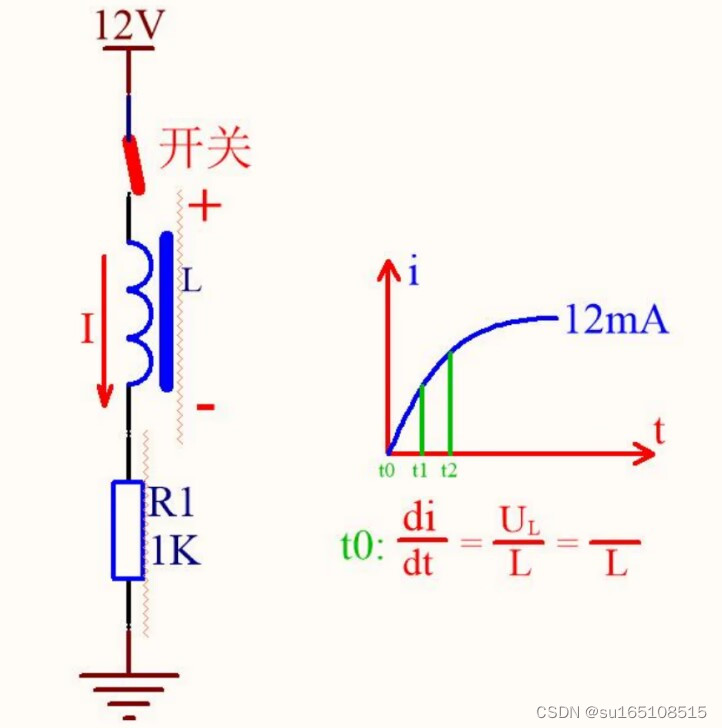
在t0时刻,由于是刚刚上电,这一瞬间电流为0,所以,电感上端的电压就是12V,电感下端的电压就是0V,由于这一瞬间,电流为0,所以电阻两端的电压Ur = 0V。
所以,我们知道了电感电压UL=12V,根据刚才的公式 ,电感电流的变化速度di/dt=UL/L=12V/L,对吧,L肯定是一个常数,我们不管是多少。
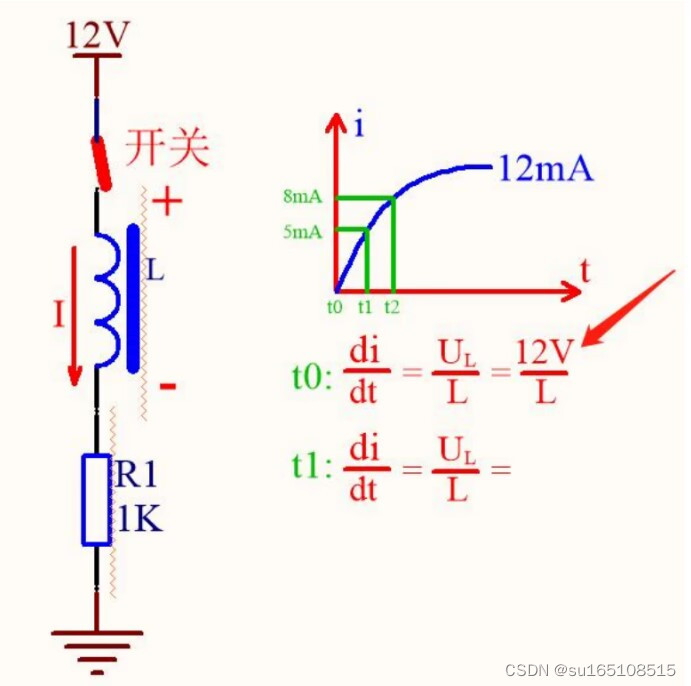
那么,现在,我们假设在t1时刻,对应回路中的电流是5mA,请问此时电流的变化速度di/dt是多大?
由于我们假设的 t1 时刻回路中的电流是 5mA,所以电阻两端的电压就是Ur = 5mA*1k = 5V
那么,很明显电感两端的电压 UL就等于:UL = U - Ur =12V - 5V =7V。
电感电压UL等于电源电压减去电阻电压,所以,t1时刻,电流变化速度di/dt等于7V/L。
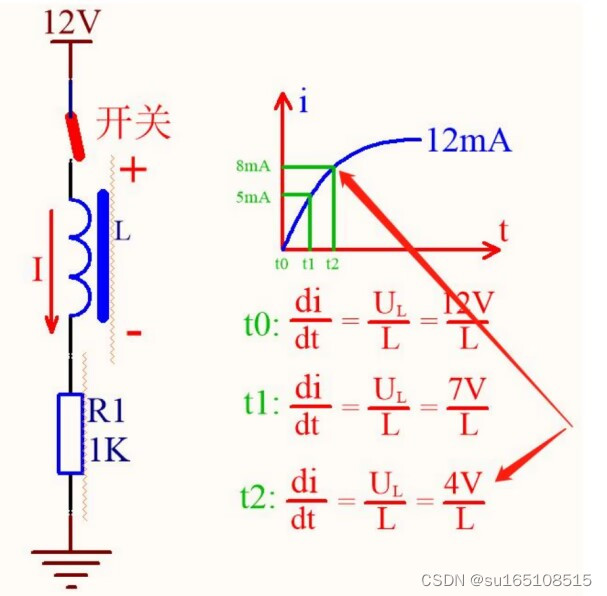
同理,我们假设t2时刻回路中的电流等于8mA,那么可以得到t2时刻回路中的电流变化速度di/dt=4V/L,观察一下,从t0到t2时刻,回路中的电流变化速度是不是越来越小的啊
我们以后就把电流变化速度称为电流斜率,这是我们通常习惯的叫法,我们发现,随着时间的推移,电流斜率会越来越小,也就是说,这个曲线刚开始的时候很陡,然后越来越缓,到最后接近一条水平线了,电流变化速度等于0,也就是电流不变了,它表明的是过了一段时间以后,电感就没有阻碍电流的作用了,电感就相当于一根导线了。