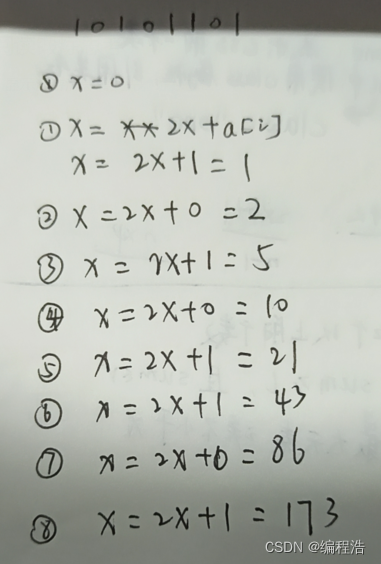题目描述
在高为 �H 的天花板上有 �n 个小球,体积不计,位置分别为 0,1,2,⋯ ,�−10,1,2,⋯,n−1。在地面上有一个小车(长为 �L,高为 �K,距原点距离为 �1S1)。已知小球下落距离计算公式为 �=0.5×�×(�2)d=0.5×g×(t2),其中 �=10g=10,�t 为下落时间。地面上的小车以速度 �V 前进。
如下图:
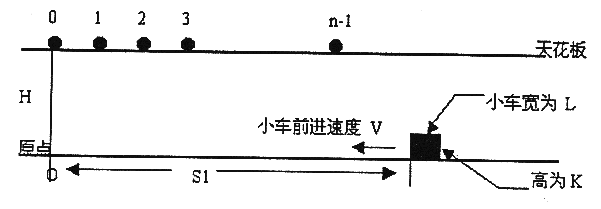
小车与所有小球同时开始运动,当小球距小车的距离 ≤0.0001≤0.0001 (感谢 Silver_N 修正) 时,即认为小球被小车接受(小球落到地面后不能被接受)。
请你计算出小车能接受到多少个小球。
输入格式
�,�1,�,�,�,�H,S1,V,L,K,n(1≤�,�1,�,�,�,�≤1000001≤H,S1,V,L,K,n≤100000)
输出格式
小车能接受到的小球个数。
输入输出样例
输入 #1复制
5.0 9.0 5.0 2.5 1.8 5
输出 #1复制
1
说明/提示
当球落入车的尾部时,算作落入车内。
【题目来源】
NOIP 2002 提高组第三题
震惊,我居然在信息里推物理式子
其实这一题出题人比较良心,没有卡精度,用double就能过。但这题坑点还是有的。
首先让我们来推式子。
对于任意一个小球,下落的时间是一样的,从公式
�=0.5×�×(�2)d=0.5×g×(t2)
可得
�=�0.5�t=0.5gd
因为这题很良心,把�g设为10,于是有
�=�5t=5d
因为球只要�x轴和车有重合且在那一瞬间的高度ℎ0h0满足�>=ℎ0>=0k>=h0>=0小车即可接住这个球~~(居然不会被车头撞飞)~~,所以小车可以接住小球的时间�0t0满足
ℎ5>=�0>=ℎ−�55h>=t0>=5h−k
然后我们就算这个时间段内小车穿过了多少个小球的�x轴就行了,但这似乎有些难度,我们可以把它转换成求哪个编号的球小车最早可以接住,哪个编号的球小车最晚可以接住。
首先根据上面哪个公式可以得到
����=ℎ−�5tmin=5h−k
����=ℎ5tmax=5h
最早接住的球的编号��ib为���(�1−����∗�+�)int(s1−tmin∗v+l),记住这里要加上l,因为最早的球可以被车尾接住。
最晚接住的球的编号��ie为���(�1−����∗�)int(s1−tmax∗v)。
这里的��>��ib>ie所以答案应该是��−��ib−ie
然后我们就有代码了
#include<bits/stdc++.h>
using namespace std;
int n;
double h,s1,v,l,k;
int main()
{
cin>>h>>s1>>v>>l>>k>>n;
double t_max=sqrt(h/5);
double t_min=sqrt((h-k)/5);
int i_b=int(s1-t_min*v+l),i_e=int(s1-t_max*v);
cout<<i_b-i_e;
}
但是到这里就结束了吗?
我们可以发现这份代码连样例都过不了,因为存在一些特殊情况,如
��>�ib>n
或是
��<0ie<0
也就是我们把一些没有球的�x轴也算成有球并被小车接住了。但这个问题其实很好解决,因为我们只要把极端的��ib和��ie处理到边界上就行了。因此,使
��=���(��,�)ib=min(ib,n)
��=���(��,0)ie=max(ie,0)
就行了。
然后就是真正的��AC代码了
#include<bits/stdc++.h>
using namespace std;
int n;
double h,s1,v,l,k;
int main()
{
cin>>h>>s1>>v>>l>>k>>n;
double t_max=sqrt(h/5);
double t_min=sqrt((h-k)/5);
int i_b=int(s1-t_min*v+l),i_e=int(s1-t_max*v);
i_b=min(i_b,n);i_e=max(i_e,0);
cout<<i_b-i_e;
}