原题链接

本题我们先需要知道
十进制 如何转 二进制
二进制 如何转 十进制

十进制 如何转 二进制：

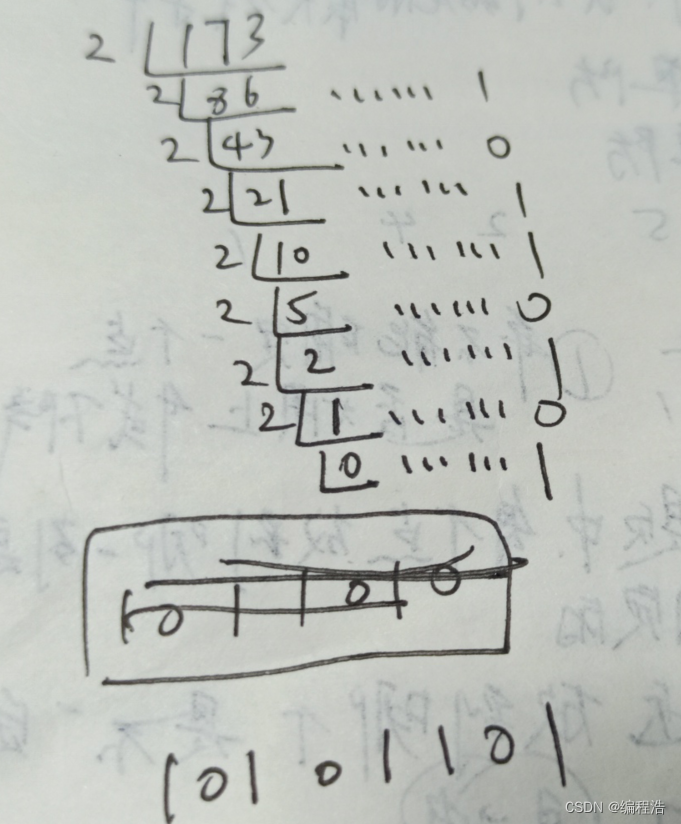
十进制转成二进制

例如 173 转成 二进制
就把173 短除法 除到0 然后 得到的余数，从下往上写

二进制 转成 十进制

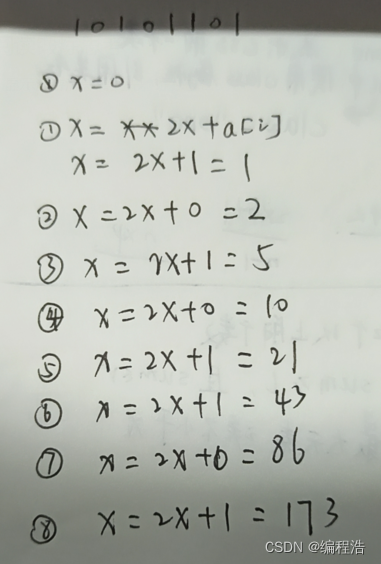
利用如图方法，把二进制 转成 十进制

本题是高精度，如何做？

由于本题的 数据是1000位，
那么 1000位的数 / 2 是需要高精度除法
以及需要 高精度乘法，高精度加法的

原因如上述两个图，都需要用到 乘法，除法，加法

注意：

1. 把初始数据a，每一位从大到小或者从小到大，入vector都可以，但是除法的时候，注意是从高位除起
2. 剩下的就是正常的 高精度算法

#include <iostream>
#include <cstring>
#include <algorithm>
#include <vector>

using namespace std;

vector<int> div(vector<int>& A, int b, int& r)
{
    vector<int> C;
    r = 0;
    for (int i = A.size() - 1; i >= 0; i -- )
    {
        r = r * 10 + A[i];
        C.push_back(r / b);
        r %= b;
    }
    reverse(C.begin(), C.end());
    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

vector<int> mul(vector<int>& A, int b)
{
    vector<int> C;
    for (int i = 0, t = 0; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i] * b;
        C.push_back(t % 10);
        t /= 10;
    }

    while (C.size() > 1 && C.back() == 0) C.pop_back();
    return C;
}

vector<int> add(vector<int>& A, int b)
{
    vector<int> C;
    for (int i = 0, t = b; i < A.size() || t; i ++ )
    {
        if (i < A.size()) t += A[i];
        C.push_back(t % 10);
        t /= 10;
    }
    return C;
}

void print(vector<int>& A)
{
    for (int i = A.size() - 1; i >= 0; i -- )
        cout << A[i];
    cout << endl;
}

int main()
{
    string a;
    cin >> a;

    vector<int> A;
    for (int i = a.size() - 1; i >= 0; i -- ) A.push_back(a[i] - '0');

    vector<int> B;
    while (A.size() > 1 || A[0] > 0)
    {
        int r;
        A = div(A, 2, r);
        B.push_back(r);
    }

    vector<int> C;
    for (int x: B)
    {
        C = mul(C, 2);
        C = add(C, x);
    }

    print(C);

    return 0;
}