⭐前言⭐
※※※大家好!我是同学〖森〗,一名计算机爱好者,今天让我们进入练习模式。若有错误,请多多指教。更多有趣的代码请移步Gitee
👍 点赞 ⭐ 收藏 📝留言 都是我创作的最大的动力!
题目
27. 移除元素
题目:
给你一个数组 nums 和一个值 val,你需要 原地 移除所有数值等于 val 的元素,并返回移除后数组的新长度。
不要使用额外的数组空间,你必须仅使用 O(1) 额外空间并 原地 修改输入数组。
元素的顺序可以改变。你不需要考虑数组中超出新长度后面的元素。
示例1
输入:nums = [3,2,2,3], val = 3
输出:2, nums = [2,2]
解释:函数应该返回新的长度 2, 并且 nums 中的前两个元素均为 2。你不需要考虑数组中超出新长度后面的元素。
示例2
输入:nums = [0,1,2,2,3,0,4,2], val = 2
输出:5, nums = [0,1,4,0,3]
解释:函数应该返回新的长度 5, 并且 nums 中的前五个元素为 0, 1, 3, 0, 4。注意这五个元素可为任意顺序。
提示
- 0 <= nums.length <= 100
- 0 <= nums[i] <= 50
- 0 <= val <= 100
思路
题目分析:
- 去除掉数组 nums 中 值为 val 的元素,返回新数组的长度;
- 不能使用额外数组空间,因为要删除元素,新数组的长度 一定小于等于 原来数组元素,我们可以在原数组上进行操作
- 元素的顺序可变,这个是我们进行优化的关键
- 由提示可知,根据相关数据的范围,本题可以直接使用int类型
由于数组的元素在内存地址中是连续的,不能单独删除数组中的某个元素,只能覆盖;
解法一:使用暴力破解,用两层循环,第一层循环用于 寻找数组中等于 val 的元素,第二层循环负责如果第一层循环找到等于 val 的元素,就将该元素后面的元素向前一步,覆盖掉该元素;
解法二: 使用快慢指针,定义 fast = slow = 0; fast 指针用来查询当前数组的元素的值 是否为 val 如果 等于 val 就 跳过该元素,如果不等就将该元素赋值给 slow ,有此可知 slow 前面的元素都是值 不为 val 的元素,返回slow 就是新数组的长度;
解法三: 使用相向双指针,题解二中如果数组中没有val 元素那么fast 和slow 都会遍历一遍数组,会遍历两遍数组,但由于题目说明的是元素的顺序可变,我们可以用双指针分别从前向后(left),和从后向前遍历(right) 当 right 和 left 相遇的时候说明遍历了数组,我们要做的就是将left 遍历到 值等于 val 的元素和right 遍历的不等于 val 的值进行互换,这样就不用一个一个地移动元素,但是缺点却是改变了元素的原有顺序位置;
解法一:暴力破解
使用双层 for 循环
- 第一层 for 循环 遍历数组元素
i = 0; i < len; i ++
- 第二层for循环 更新数组元素
如果 nums[i] == val
for(int j = i + 1; j < len ; j++) nums[j - 1] = nums[j];
将i后面值向前一位进行覆盖;
程序源码
// 时间复杂度: O(n^2)
// 空间复杂度: O(1)
public class Solution {
public static int removeElement(int[] nums, int val) {
// 双重循环
int len = nums.length;
for (int i = 0; i < len; i++) { // 第一层循环, 查找值为 val 的元素
if (nums[i] == val) { // 找到值为 val 的元素, 将i后面的元素集体向前移动一位
for (int j = i + 1; j < len; j++) {
nums[j - 1] = nums[j]; // 注意 j的起始值 和 结束条件
}
i--; // 因为 i 以后的元素都集体向前移动一位, 此时位于下标 i 的元素, 其实是下标为i + 1的元素,需要重新遍历;
len--; // 覆盖一个元素, 数组的长度 - 1;
}
}
return len; // 返回数组的长度;
}
}
例:nums = [0,1,2,2,3,0,4,2], val = 2 移除 nums 中的 2
使用暴力破解删除过程为:
初始化:i = 0
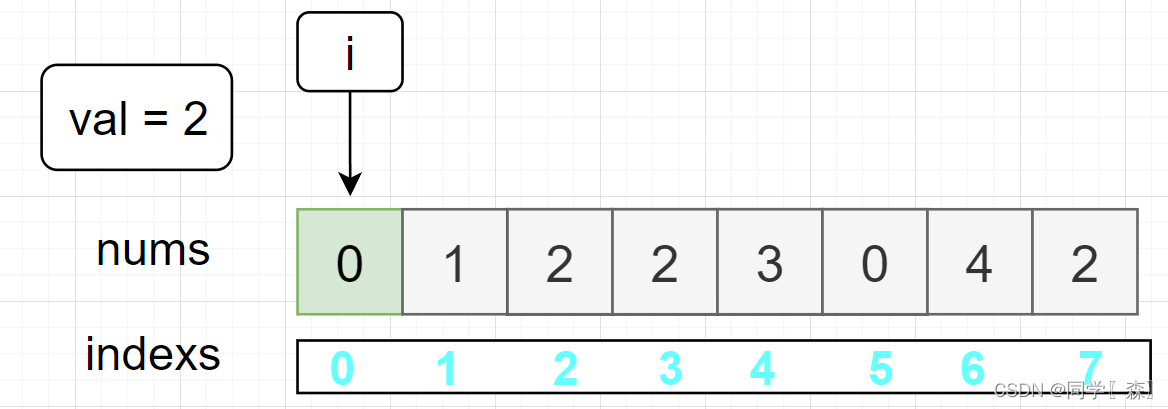
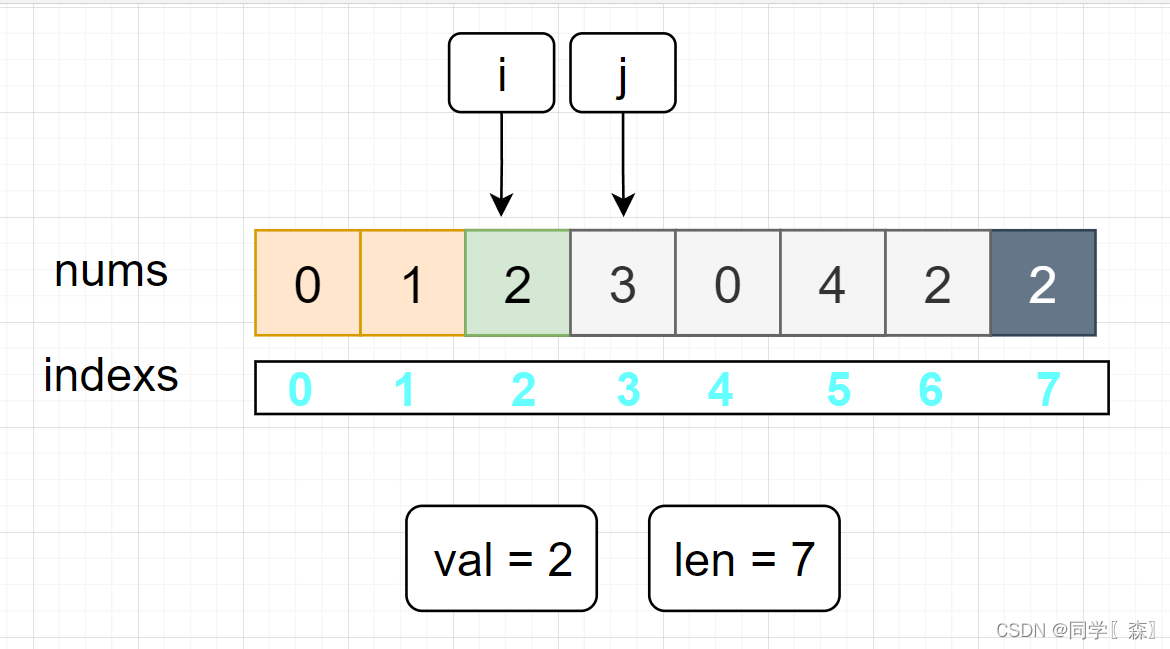
当 i = 0, 1时 nums[ i ] != 2 不执行if 语句 i = 2 时,进入if语句 j = i + 1;
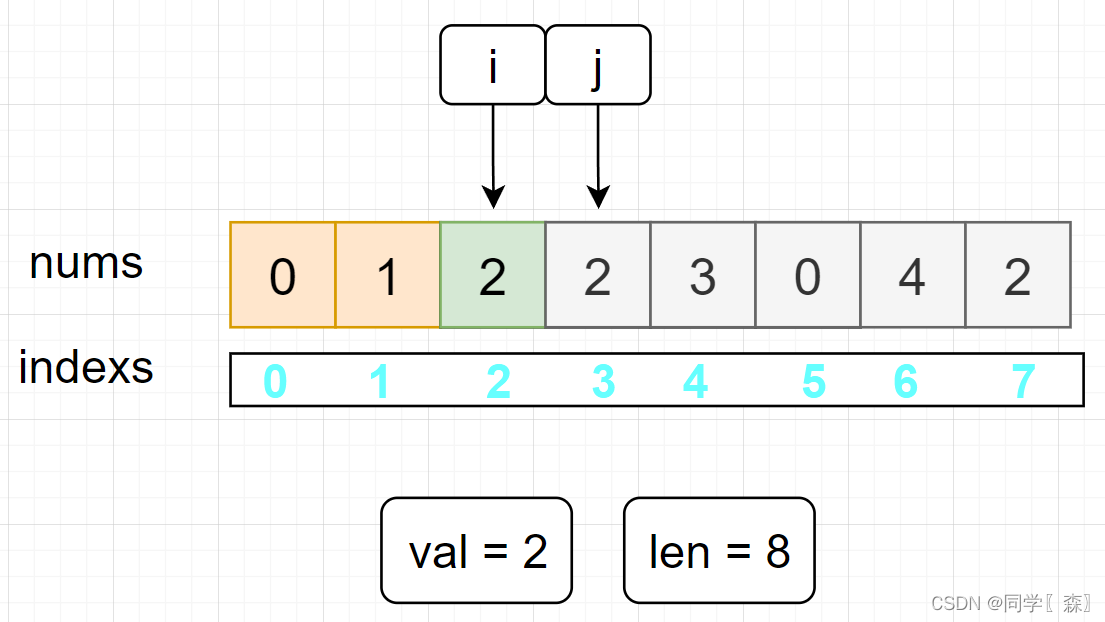
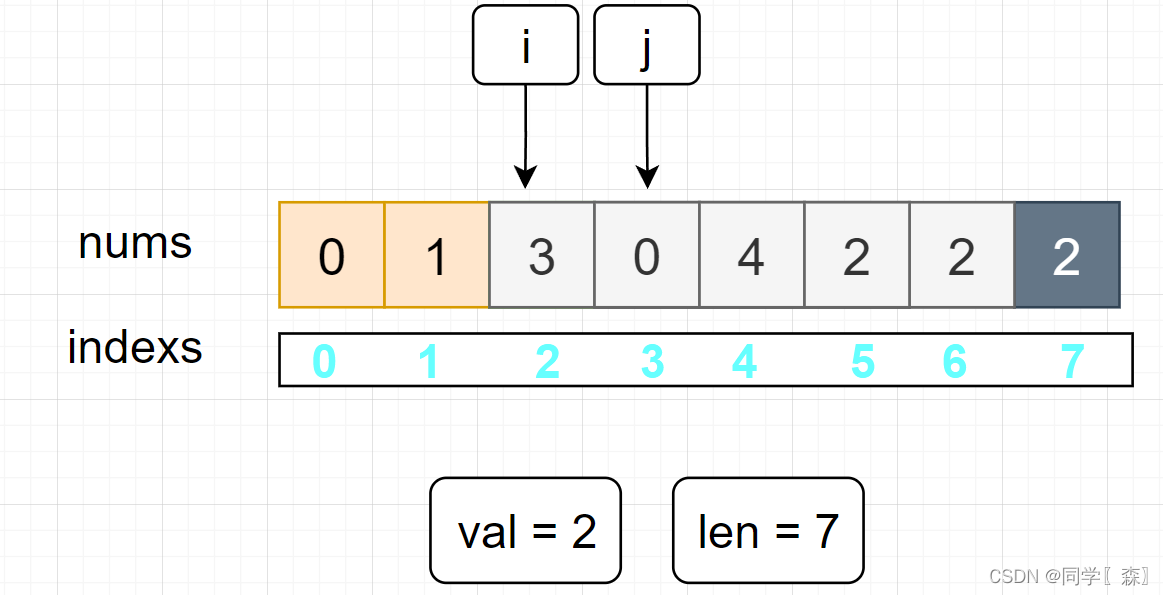
执行 第二层循环 更新数组元素 : 将 i 后面的所有元素集体想前移动一位
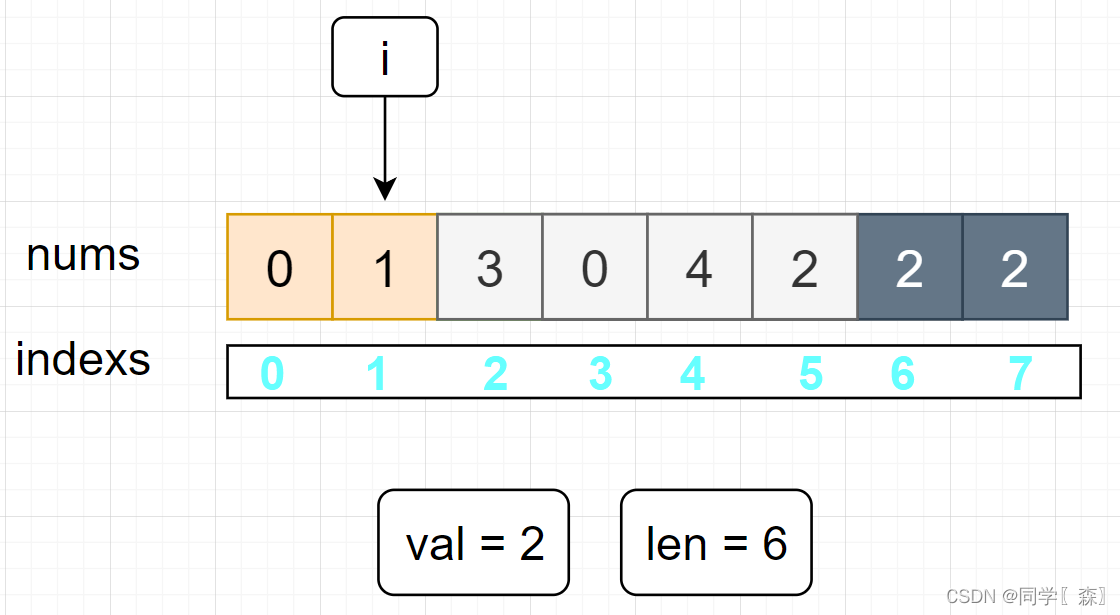
此时灰色的框的元素 2 仍然存在数组中,我们需要将数组的长度由 8 改为 7 将最后一个元素 删除掉
注意 for循环的结束条件 是i < len而不是i < nums.length
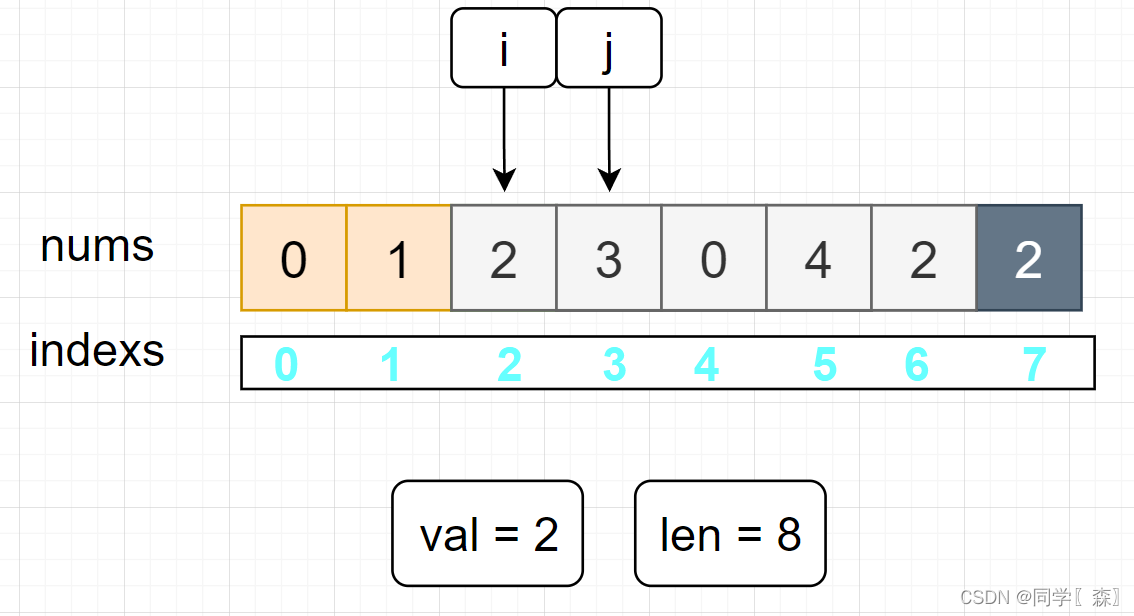
i --; len--;
这里需要重新遍历 下标为 2 的元素 需要 i-- 向前一步,同时 新数组的长度变成了7 循环到 下标为 6的时候就结束了,
注意要在循环的过程中更新结束的len值
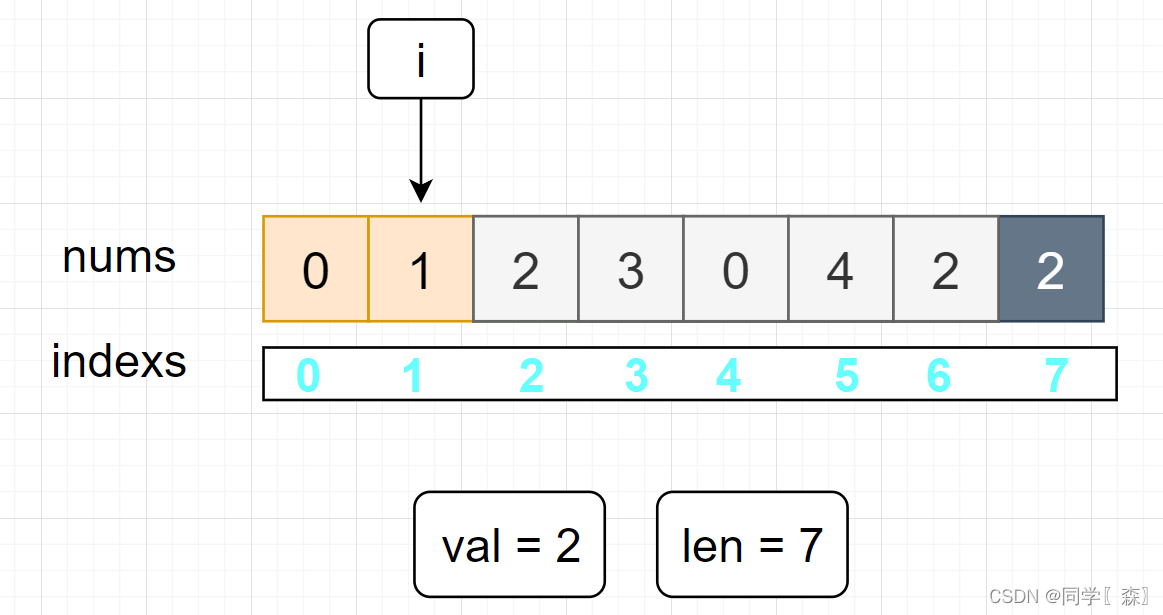
i++ i = 2; 重复上述过程

接下来过程和 i = 0 ,i 时一样 i 一直++到 i == 5
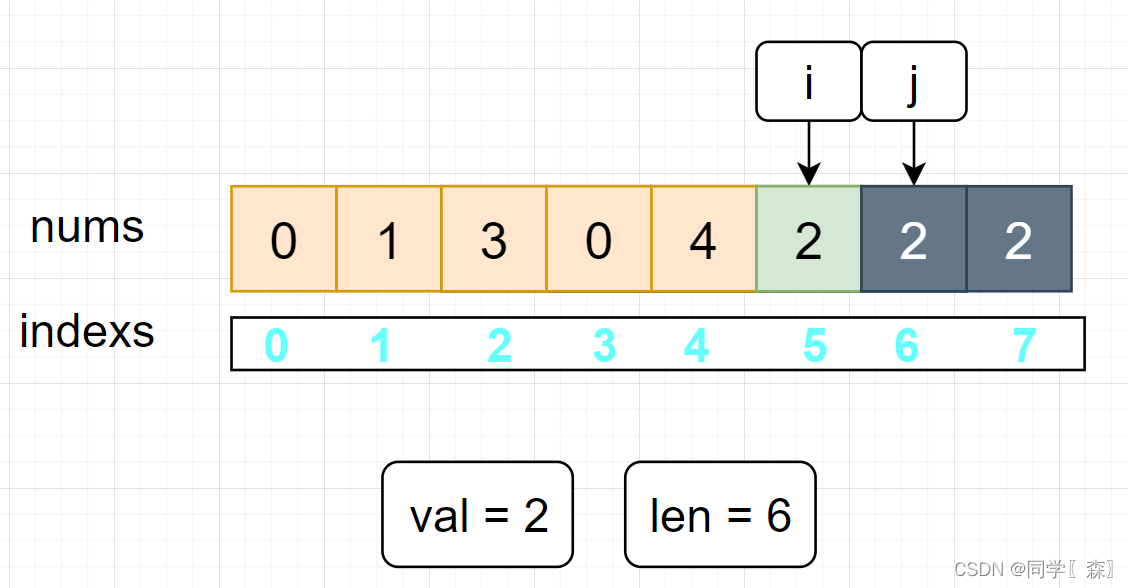
此时 j = 6 = len 不进入第二层for循环 执行
i--和len--操作
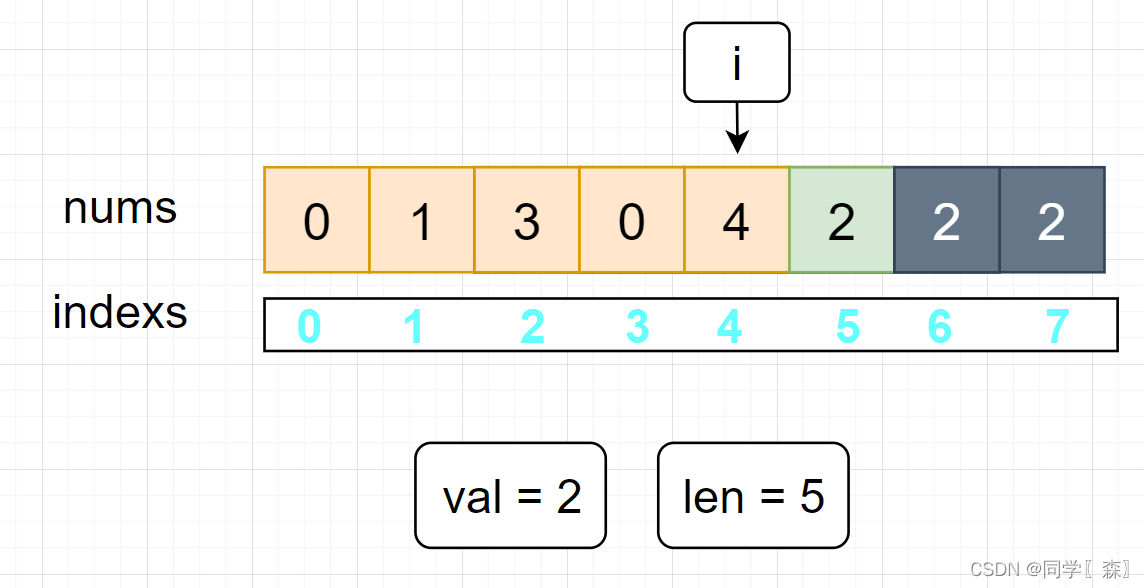
此时 i ++ 后 i = 5 i = len 不满足进入第一层for循环条件,跳出循环 新数组长度为 5 元素分别是:0 1 3 0 4 符合预期;
使用暴力破解 的时间复杂度 为:O(n^2) 时间复杂度较高,我们能不能进一步优化下;
解法二:快慢指针(双指针)
快慢指针: 通过一个快指针和一个慢指针在一个for循环下完成两个for循环的工作
定义快慢指针:
- 快指针: 寻找新数组的元素,即元素的值不等于 val 的元素,
- 慢指针: 指向更新 新数组下标的位置,即新数组的最后一个元素的下一个的位置,和新数组的长度相等
思路: 快指针查询不等于val的元素,将这些数组赋值给慢指针所在的位置,如果查询到等于 val 的元素,快指针就跳过该元素;
完整代码:
// 时间复杂度: O(n)
// 空间复杂度: O(1)
public class demo2 {
public static int removeElement(int[] nums, int val) {
// 这种实现方法没有改变元素的相对位置
int slow = 0;
for (int fast = 0; fast < nums.length; fast++) {
if (nums[fast] != val) {
nums[slow] = nums[fast];
slow++;
// 这里可以化简为 nums[slow++] = nums[fast]; ++在slow的后面, 表示先用后加
}
}
return slow;
}
}
例:nums = [0,1,2,2,3,0,4,2], val = 2 移除 nums 中的 2
图解:
初始化:
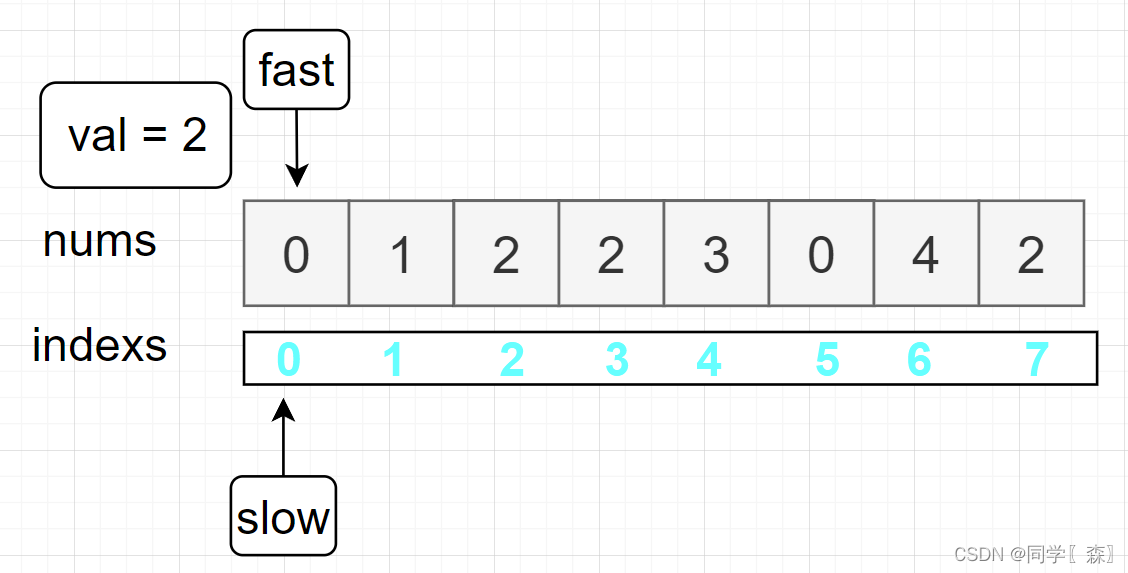
nums[fast] != val 0 != 2 nums[slow] = nums[fast];
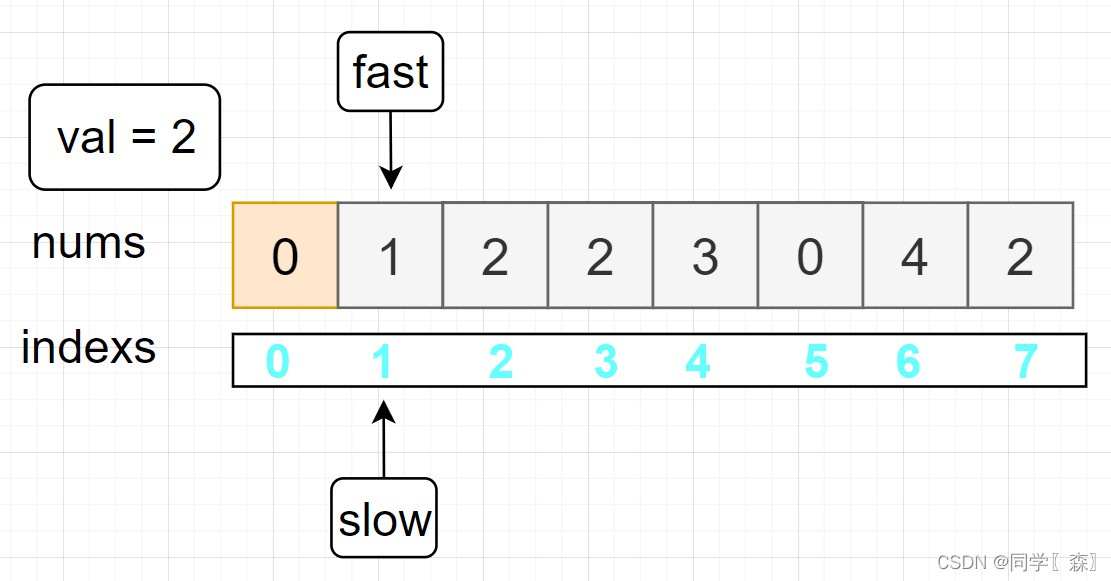
fast = 1; nums[1] != val
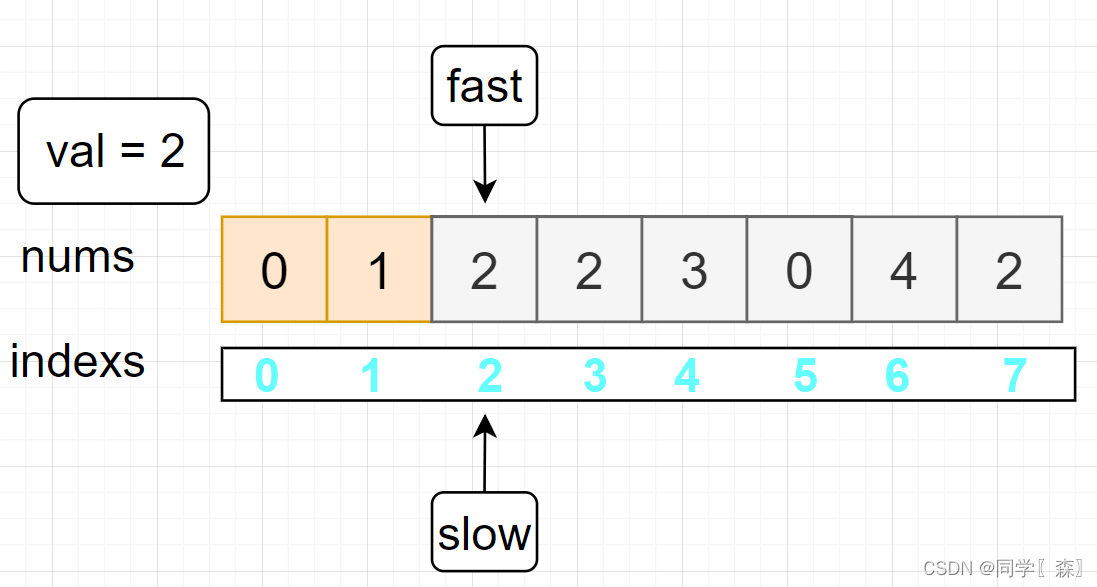
fast = 2 nums[2] == val
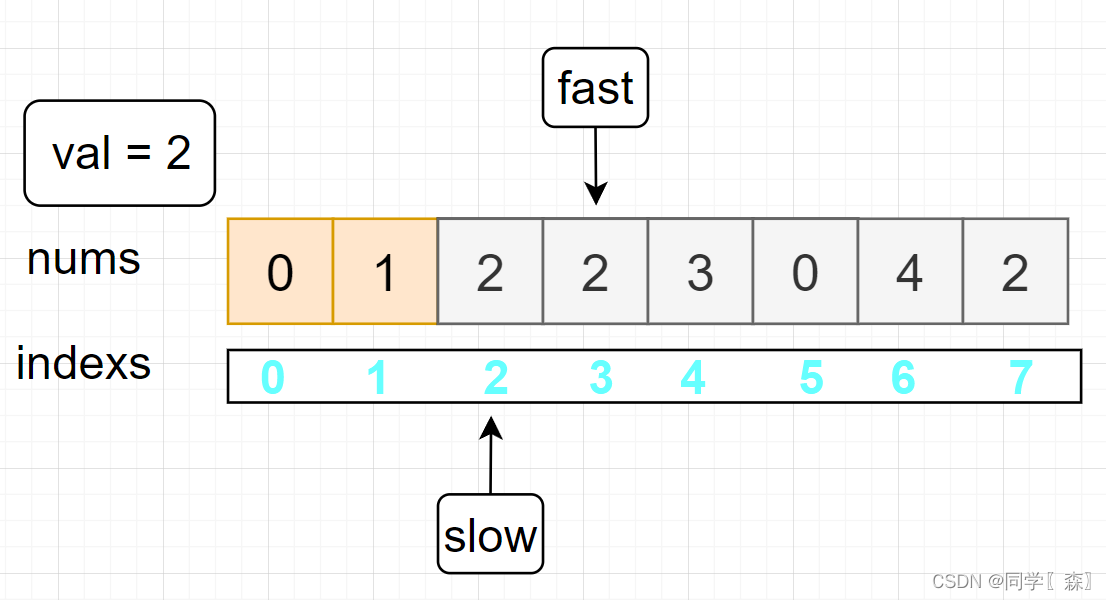
fast == 3 nums[3] == val
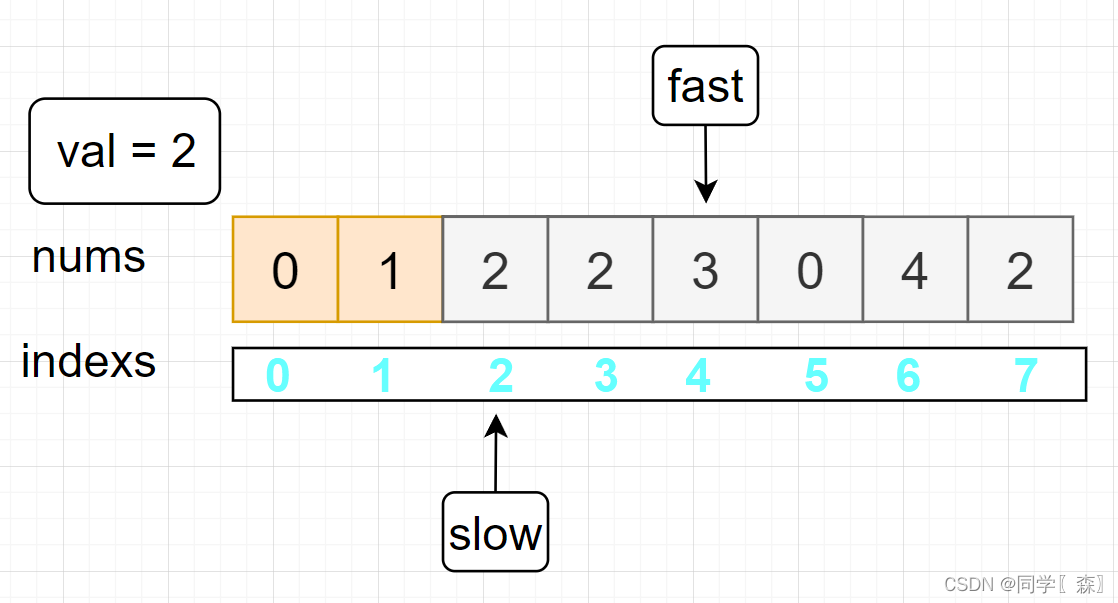
fast == 4 nums[4] != 2
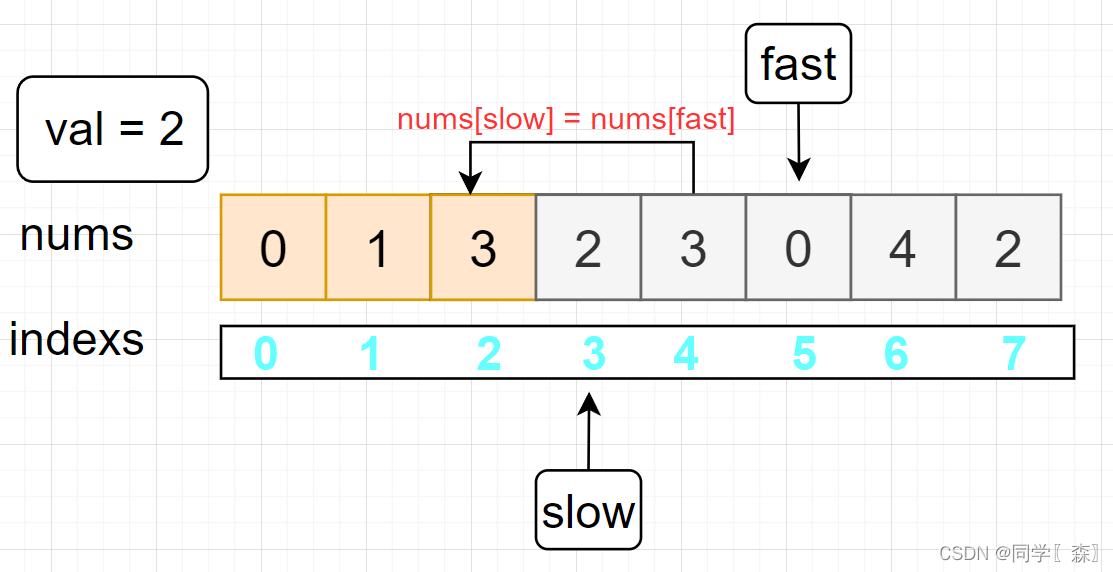
fast = 5 nums[5] != val
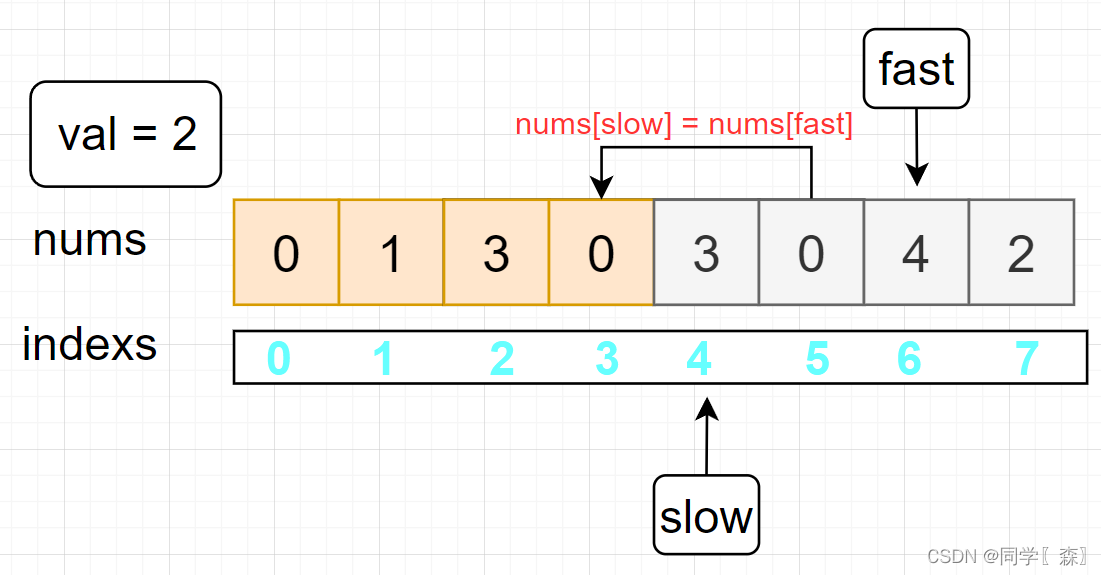
fast = 6 nums[6] != val
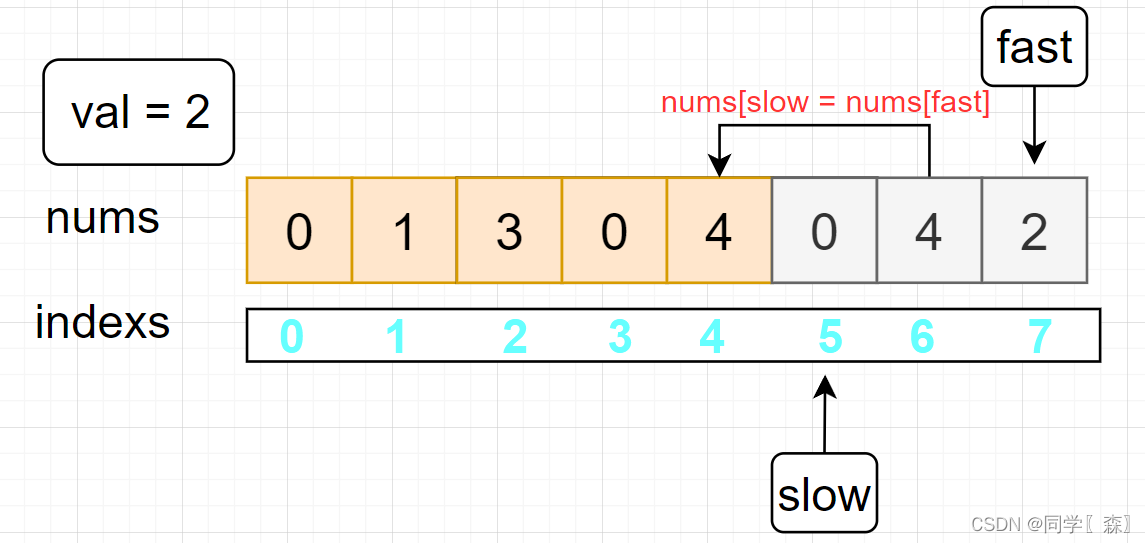
fast = 8 nums[7] == val
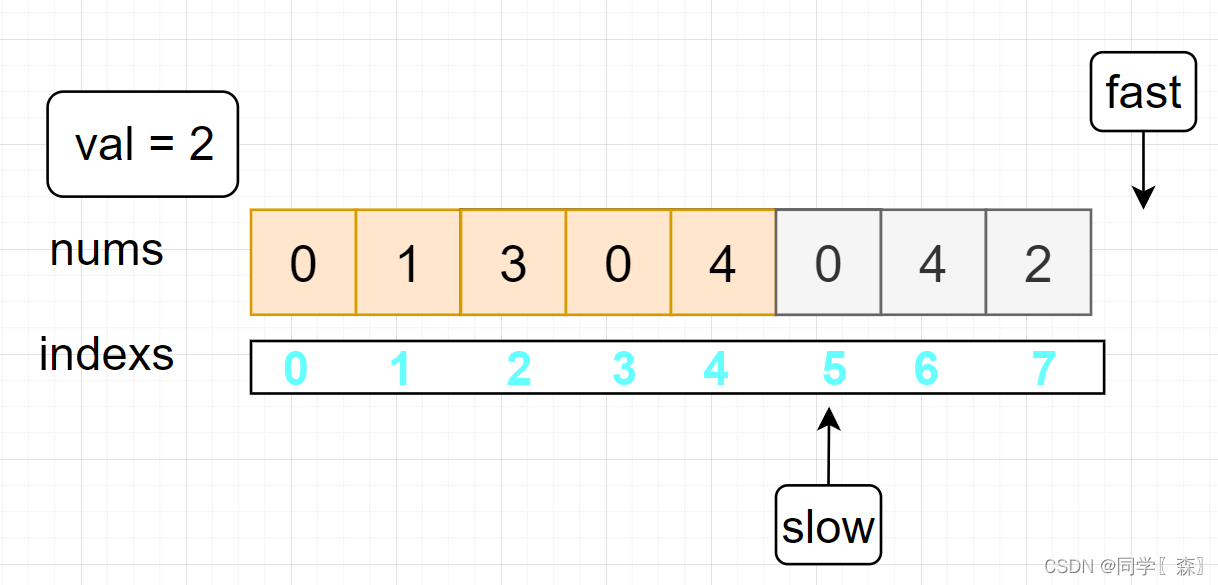
fast = 8 == nums.length 跳出循环
此时slow 所值的下标位置,正好等于新数组(橙色部分)的长度;
将slow返回;
这次解法比上一次解法时间复杂度直接从O(n^2) 降低到 O(n)但这种算法在最坏情况下(数组没有元素等于val)需要左右指针各遍历一次数组,遍历了两次数组,而且还进行了无效复制 nums[slow] = nums[fast](fast == slow时)
解法三:双指针优化
相向双指针:通过左右两个指针,向中间遍历实现只遍历一次完成删除的工作
- 前提: 元素的顺序可以改变
- 思路:如果要移除的元素在数组开头,我们可以直接从后面不排除的元素移动到开头这个元素的位置
例:【3 4 6 2 7 8】 val 3 我们直接可以用 8 来替代 3 得到 【8 4 6 2 7】同样满足题目
这个优化在序列中val 元素的数量较少时效果较明显;
实现 :
- 使用left = 0; right = nums.length; 向中间遍历,
- 如果 left 指向的元素等于 val 就将 right 指向的元素 复制到left的位置,然后right–;
- 如果 left 指向的元素 不等于 val, 就left ++
- 会有一种情况是right 指向的元素也等于 val ,不过没有关系,因为上一步中 没有left++;还会检查新复制来的元素是不是为val;
- 当left 和 right重合的时候就遍历完数组中所有元素,结束循环
完整代码
// 时间复杂度: O(n)
// 空间复杂度: O(1)
public class Solution {
public static int removeElement(int[] nums, int val) {
int left = 0; // 指向数组第一个元素
int right = nums.length - 1; // 指向数组最后一个元素
while(left <= right){
if (nums[left] == val) {
// 如果 left 所指向的元素等于 val 就将 right 指向的元素复制到 left 的位置
nums[left] = nums[right--];
} else {
// 不等于 val, 就left++;
left++;
}
}
return left;
}
}
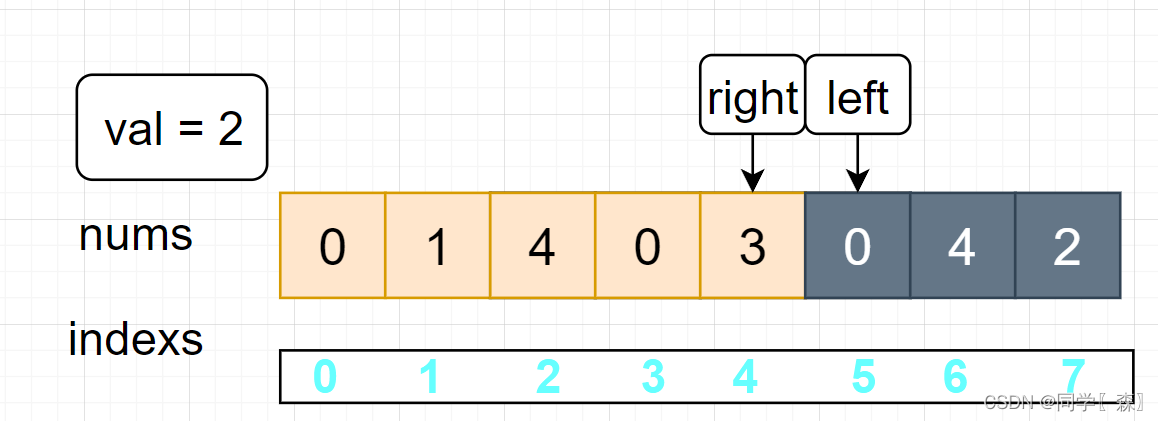
例:nums = [0,1,2,2,3,0,4,2], val = 2 移除 nums 中的 2
初始化
left = 0; right = 7
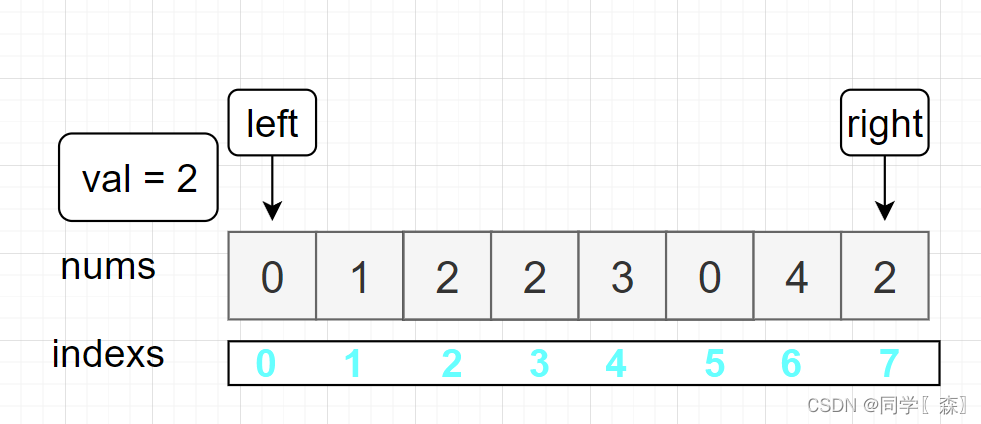
left = 0 nums[0] != val
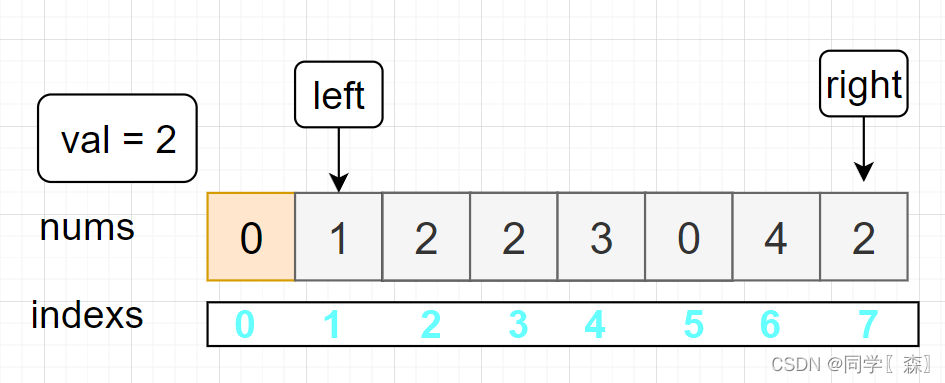
left = 1 nums[0] != val
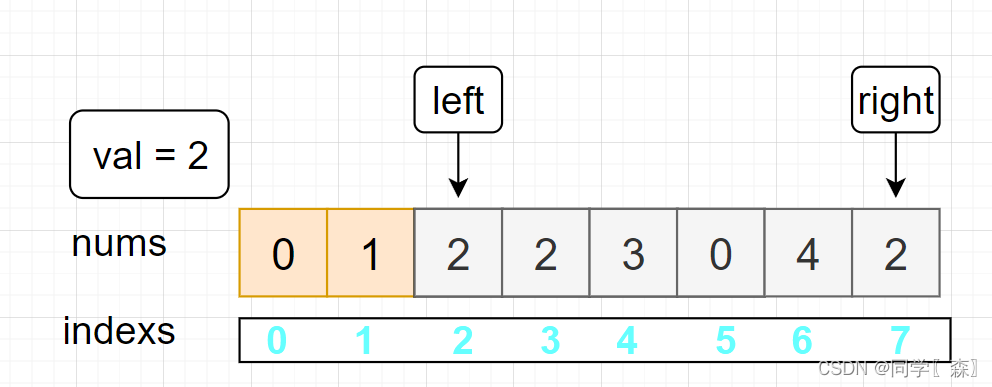
left = 2 nums[0] == val
nums[left] = nums[right–]
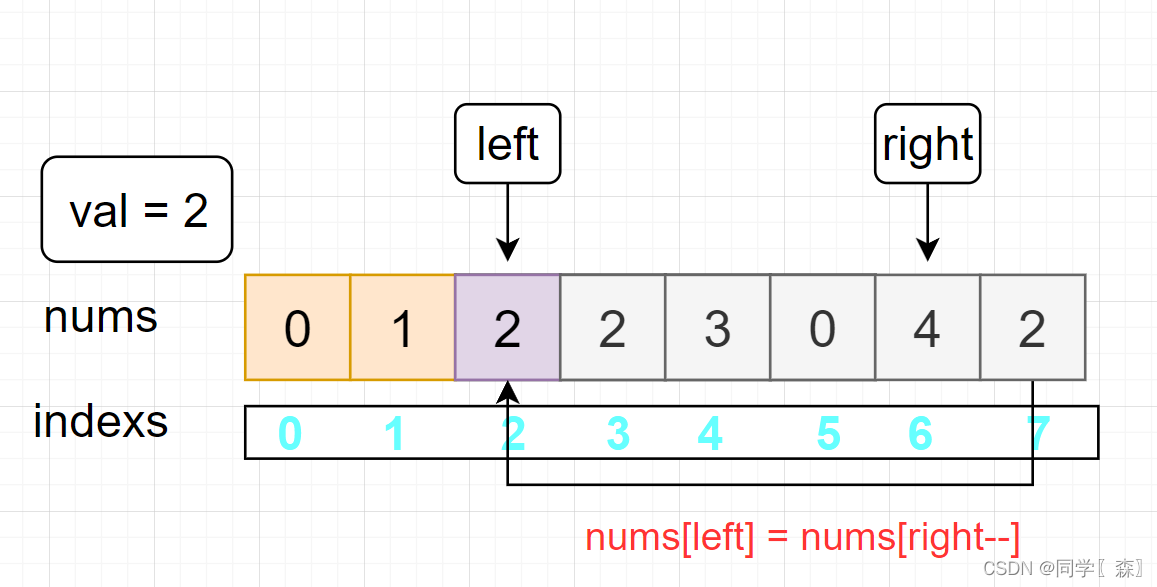
left = 2 nums[0] == val
nums[left] = nums[right–]
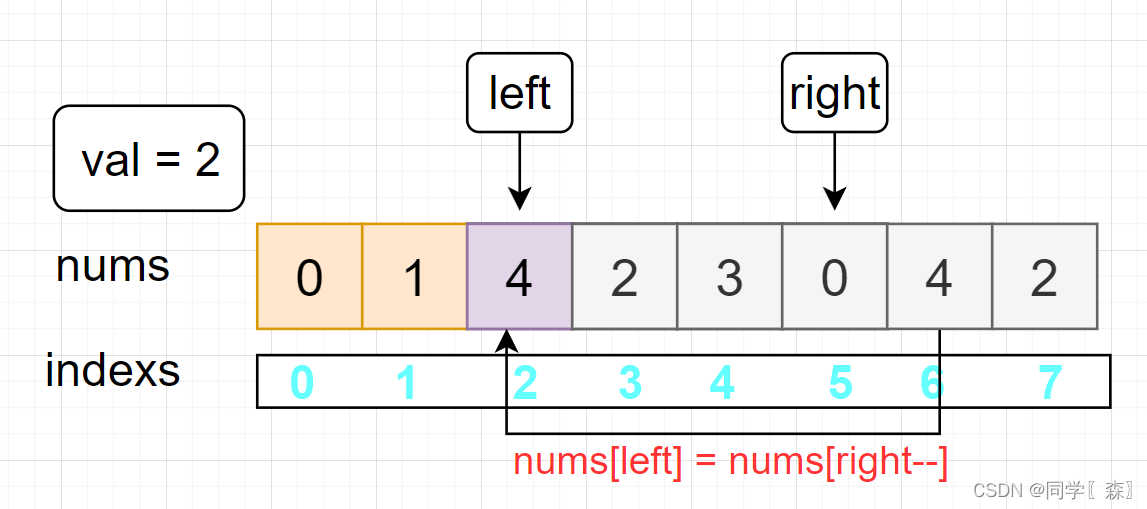
left = 2 nums[2] == 4 != 2
left++
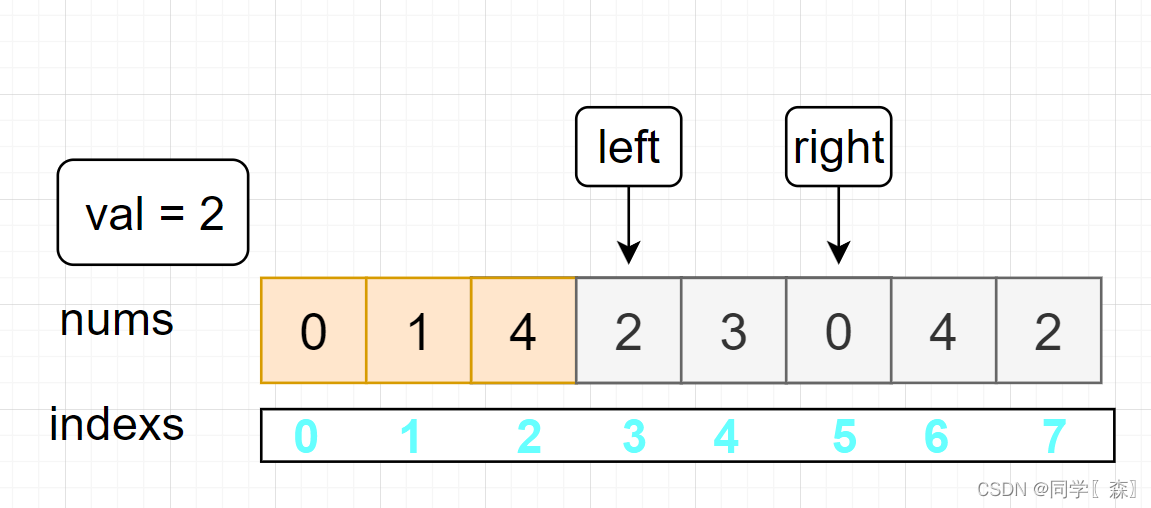
left = 3
nums[3] = 2 == val
nums[left] = nums[right–]
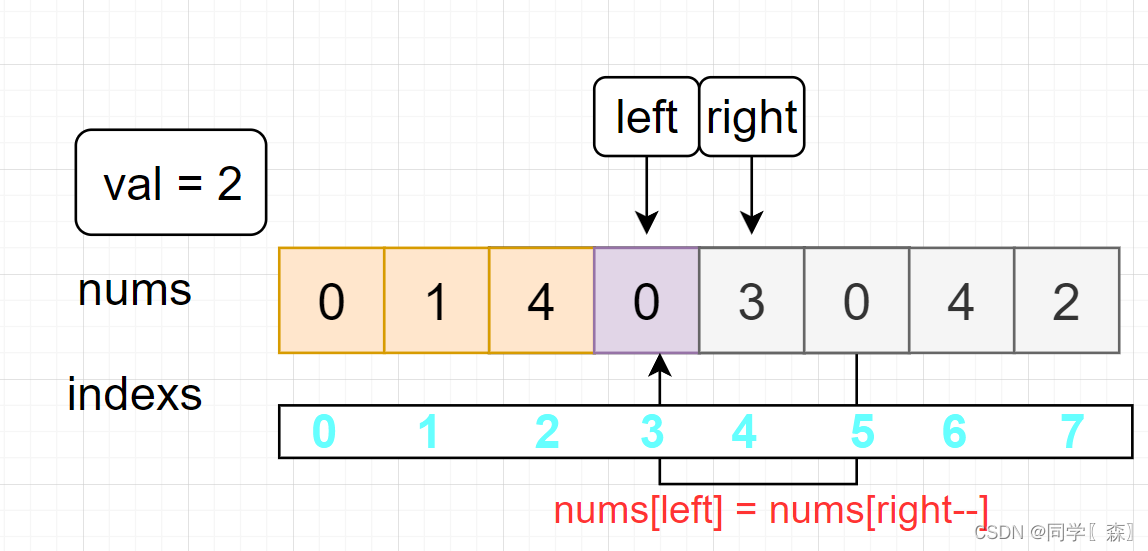
left = 3 nums[3] != val
left++;
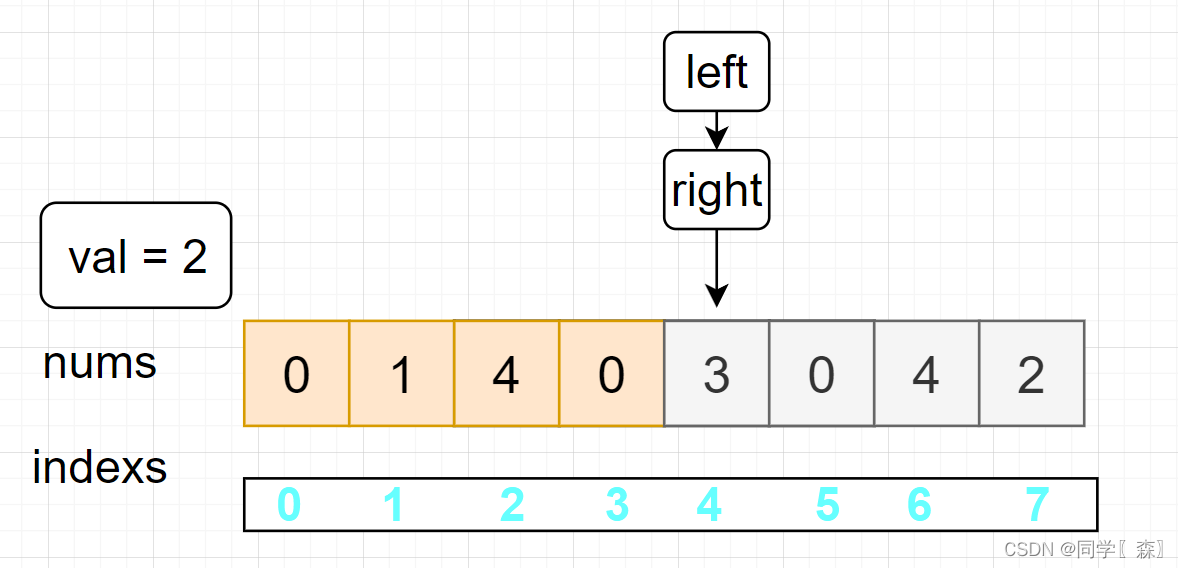
left = 4 nums[4] != val
left++;
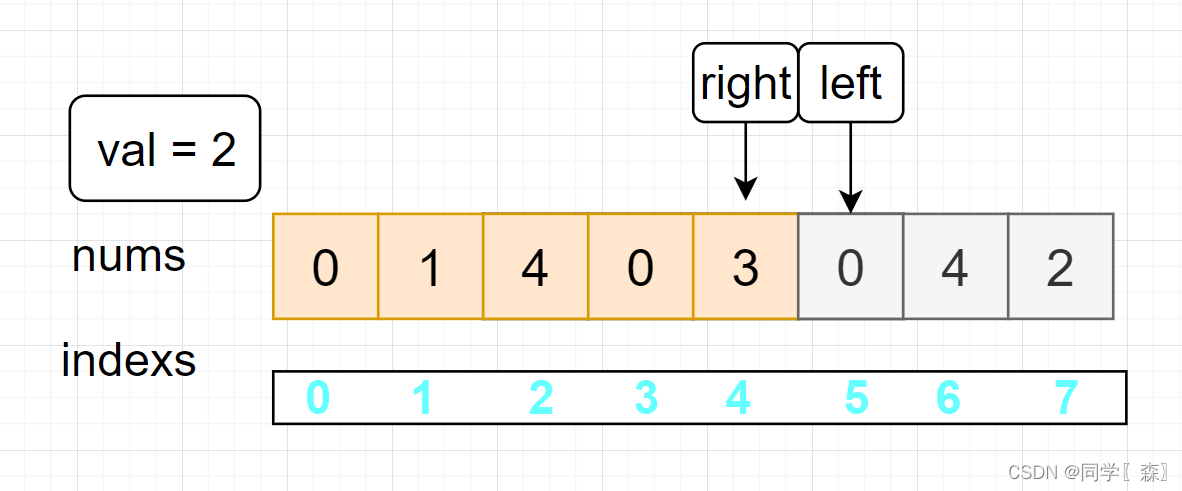
left > right
跳出循环, 返回 left ,5
这种算法两个指针在最坏的情况下合起来只遍历了数组一次,避免了需要保存的元素的重复复制操作
但是这种算法重复第判断了好几次在同一个下标位置,对于right指向的元素 等于val 的情况还复制了过去,还存在着一定的问题,所以我们还可以进行优化
寻找left 指向的元素 等于 val 和 right 指向的元素 不等于 val,这种情况下才进行复制
完整代码
// 时间复杂度: O(n)
// 空间复杂度: O(1)
public class Solution {
public static int removeElement(int[] nums, int val) {
int left = 0; // 指向数组第一个元素
int right = nums.length - 1; // 指向数组最后一个元素
while (left <= right){
while (left <= right && nums[left] != val){ // 寻找左边等于 val 的元素
left++;
}
while (left <= right && nums[right] == val){ // 寻找右边不等于 val 的元素
right--;
}
if (left < right) { // 将右边不等于val的元素覆盖掉左边等于val的元素
nums[left++] = nums[right--];
}
}
return left; // left 制定指向最终数组末尾的下一个元素;
}
}
例:nums = [0,1,2,2,3,0,4,2], val = 2 移除 nums 中的 2
图解 : 初始化
left = 0; right = 7
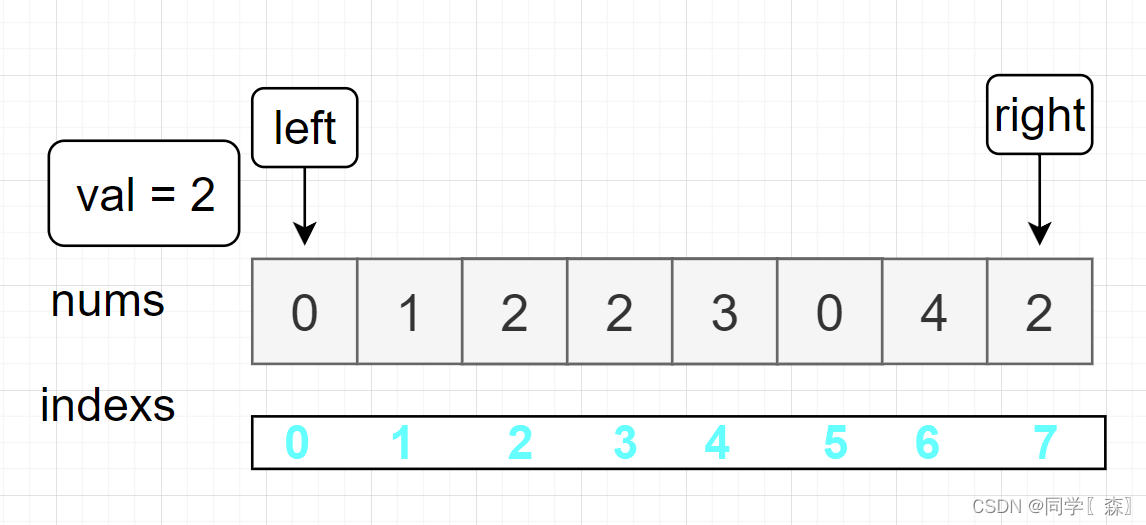
寻找左边等于 val 的元素 left = 2
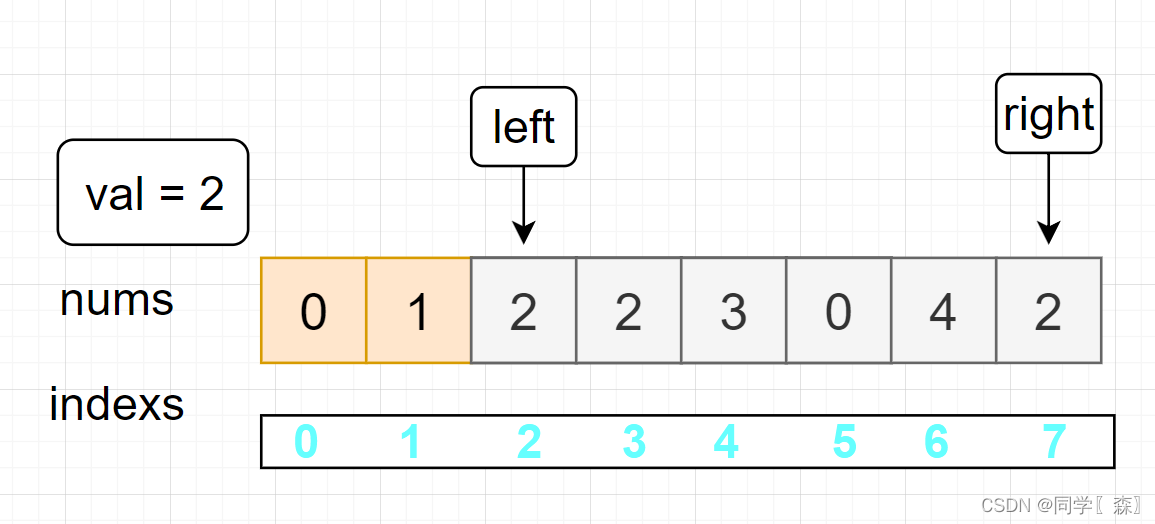
寻找右边不等于 val 的元素 right = 6
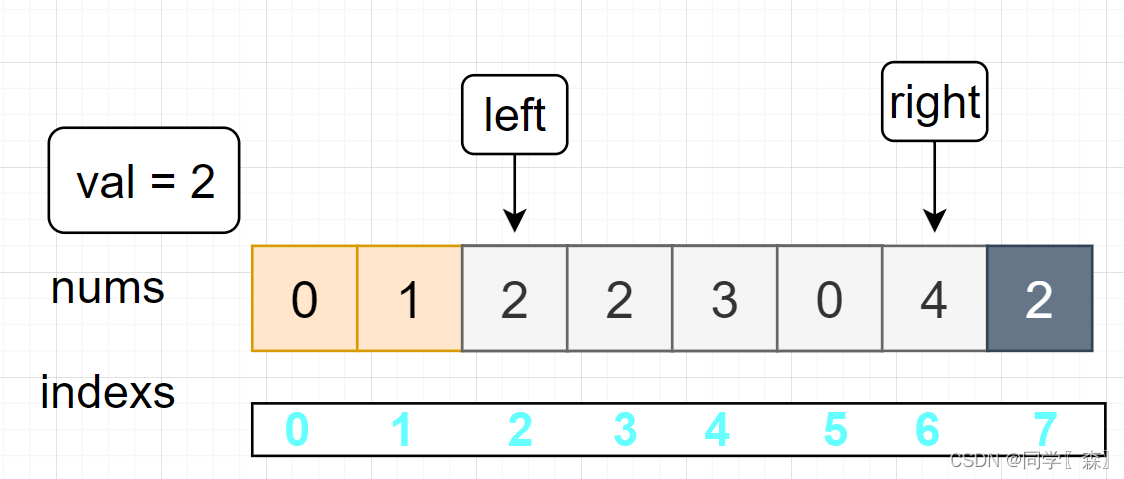
left < right
nums[left++] = nums[right–]; 将右边不等于val的元素覆盖掉左边等于val的元素
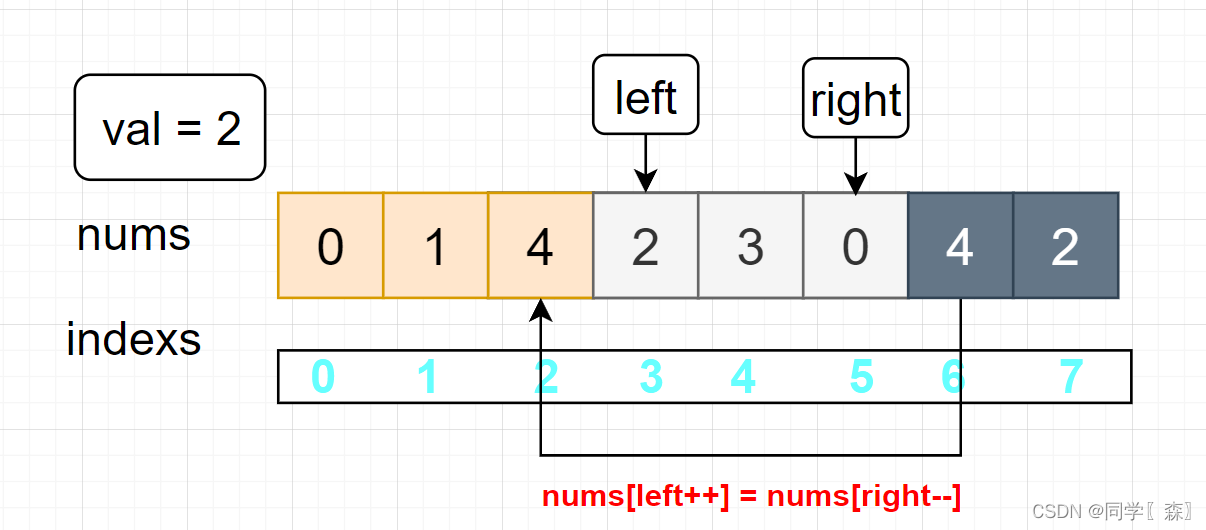
left <= right 进入循环
寻找左边等于 val 的元素 left = 3
寻找右边不等于 val 的元素 right = 5
left < right
nums[left++] = nums[right–]; 将右边不等于val的元素覆盖掉左边等于val的元素
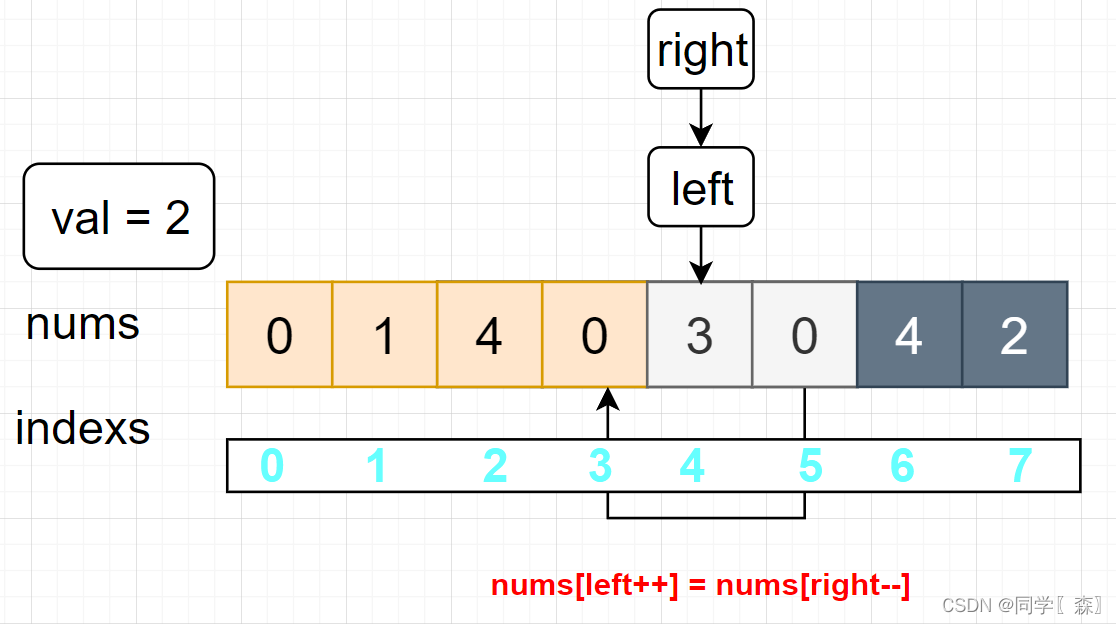
left == right 进入循环
寻找左边等于 val 的元素 left = 5
left > right跳出循环
left > right 不会进入循环 并且也不会 进行交换


![P1039 [NOIP2003 提高组] 侦探推理](https://img-blog.csdnimg.cn/img_convert/a6e0b45b676d8b20ba3321a37e64fb7d.png)








![P1037 [NOIP2002 普及组] 产生数](https://img-blog.csdnimg.cn/img_convert/7cc4e2ba95cca1686a1fe63850d84b36.png)
