北邮22信通一枚~   

跟随课程进度每周更新数据结构与算法的代码和文章 

持续关注作者  解锁更多邮苑信通专属代码~

获取更多文章  请访问专栏~

北邮22信通_青山如墨雨如画的博客-CSDN博客

目录

1.二叉树的前序遍历

1.1递归算法

1.2非递归算法

1.2.1模板类实现栈  

1.2.2模板类实现栈的优化算法

 1.2.3 STL栈

2.二叉树的中序遍历

2.1递归算法

2.2非递归算法

2.2.1模板类实现栈

2.2.2模板类实现栈的优化算法

2.2.3 STL栈

3.二叉树的后序遍历

3.1递归算法

3.2非递归算法

3.3说明

4.层序遍历

5.模板类实现栈完整代码

5.1代码部分

5.2运行结果

 6.STL实现栈完整代码

6.1代码部分

6.2运行结果：

---

1.二叉树的前序遍历

1.1递归算法

template<class temp>
void bintree<temp>::preorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		cout << r->data;
		preorder(r->leftchild);
		preorder(r->rightchild);
	}
}

1.2非递归算法

1.2.1模板类实现栈  

栈顶元素永远为当前元素的父节点，设r为当前访问的节点，则

1.若r！=NULL，访问r（cout<<s[top].r->data;)并入栈（s[++top].r=r;），调用r=r->leftchild;将r标记为1（s[top].tag=1;）返回1；

2.若r==NULL，重新设r为栈顶元素

        2.1若r标记为2，说明右子树返回；r出栈，重新设r为栈顶元素（top--;），返回2.1；

        2.2若r标记为1，说明左子树返回；调用r=r->rightchild；将r标记为2（s[top].tag=2;），返回1；

反复执行，直到栈空（top==-1），程序结束。

if(r!=NULL)

{

cout<<r->data;入栈

}

if(r==NULL)

        1.不出栈，换右支

        2.出栈

template<class temp>
void bintree<temp>::stackpreorder(binnode<temp>* r)
{
	linkstack<temp> s[100];//栈
	int top = -1;//栈顶指针
	do
	{
		while (r != NULL)//入栈并访问，设置为左子树
		{
			s[++top].r = r;
			s[top].tag = 1;
			cout << s[top].r->data;
			r = r->leftchild;
		}
		while ((top != -1) && s[top].tag == 2)//出栈
			top--;
		if ((top != -1) && (s[top].tag == 1))
		{
            //设置栈顶访问右子树
			r = s[top].r->rightchild;
			s[top].tag = 2;
		}
	} while (top != -1);
}

1.2.2模板类实现栈的优化算法

        当前节点，访问完其左子树之后，依靠当前结点找到右子树，之后当前节点不再提供信息，等待出栈；可以提前让当前结点出栈，简化递归过程。

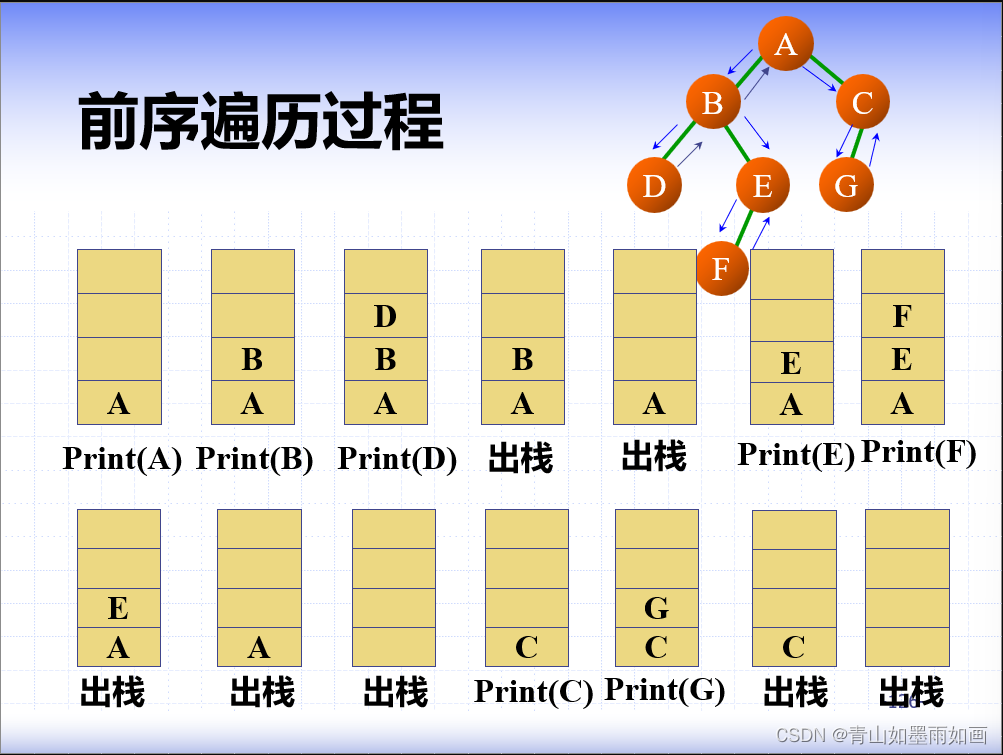
算法优化：

if(r!=NULL)

{

        cout<<r->data;入栈

}

if(R==NULL)

        出栈，换右支

template<class temp>
void bintree<temp>::quickstackpreorder(binnode<temp>* r)
{
	linkstack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			cout << r->data;
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.pop();
			r = r->rightchild;
		}
	}
}

 1.2.3 STL栈

template<class temp>
void bintree<temp>::quickSTLpreorder(binnode<temp>* r)
{
	stack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			cout << r->data;
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.top();
			s.pop();
			r = r->rightchild;
		}
	}
}

2.二叉树的中序遍历

2.1递归算法

template<class temp>
void bintree<temp>::inorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		inorder(r->leftchild);
		cout << r->data;
		inorder(r->rightchild);
	}
}

2.2非递归算法

2.2.1模板类实现栈

栈顶元素永远为当前元素的父节点，设r为当前访问的节点，则

1.若r！=NULL，r入栈（s[++top].r=r;），调用r=r->leftchild;将r标记为1（s[top].tag=1;），返回1；

2.若r==NULL，重新设r为栈顶元素

        2.1若r标记为2，说明右子树返回；r出栈，重新设r为栈顶元素（top--；），返回2.1；

        2.2若r标记为1，说明左子树返回；调用r=r->rightchild；访问r（cout<<s[top].r->data;）并将r标记为2（s[top].tag=2;），返回1；

反复执行，直到栈空（top==-1），程序结束。

if(r!=NULL)

{

        入栈；

}

if(r==NULL)

        1:cout<<r->data;不出栈，换右支；

        2:出栈

template<class temp>
void bintree<temp>::stackinorder(binnode<temp>* r)
{
	linkstack<temp> s[100];
	int top = -1;
	do
	{
		while (r != NULL)
		{
			s[++top].r = r;
			s[top].tag = 1;
			r = r->leftchild;
		}
		while ((top != -1) && (s[top].tag == 2))
			top--;
		if ((top != -1) && (s[top].tag == 1))
		{
			r = s[top].r->rightchild;
			cout << s[top].r->data;
			s[top].tag = 2;
		}
	} while (top != -1);
}

2.2.2模板类实现栈的优化算法

        当前节点，访问完其左子树之后，依靠当前结点找到右子树，之后当前节点不再提供信息，等待出栈；可以提前让当前结点出栈，简化递归过程。

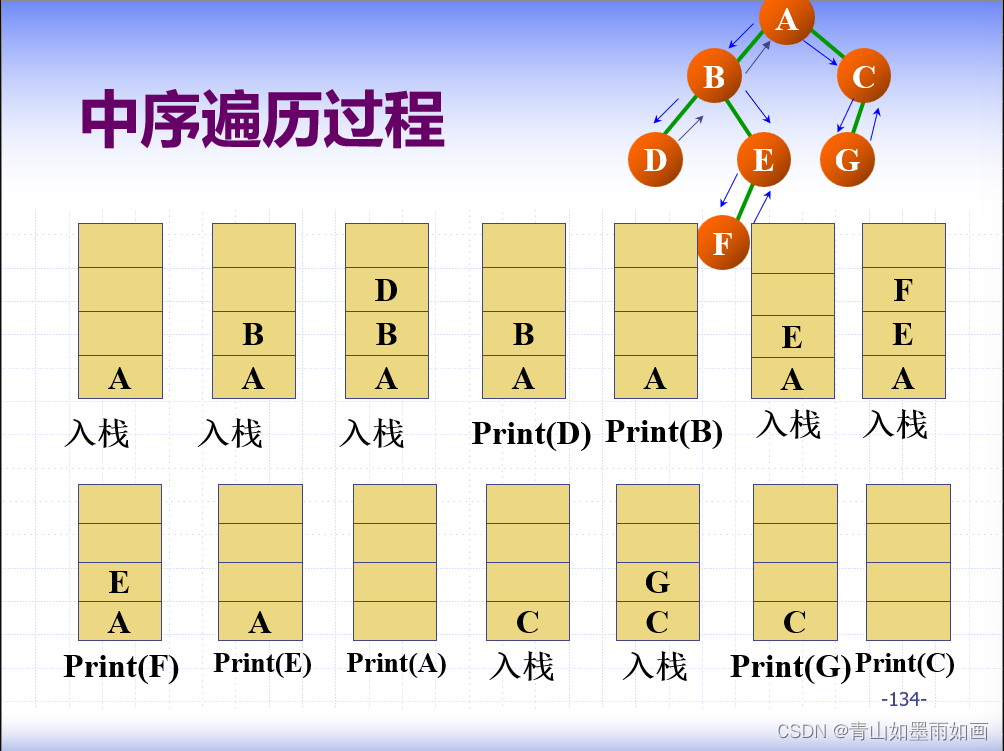
算法优化

if(r!=NULL)

{

        入栈；

}

if(r==NULL)

{

        cout<<r->data;

        出栈，换右支；

}

template<class temp>
void bintree<temp>::quickstackinorder(binnode<temp>* r)
{
	linkstack<binnode<temp>*>s;
	while (!s.empty() || r != NULL)
	{
		if (r != NULL)
		{
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.pop();
			cout << r->data;
			r = r->rightchild;
		}
	}
}

2.2.3 STL栈

template<class temp>
void bintree<temp>::quickSTLinorder(binnode<temp>* r)
{
	stack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.top();
			s.pop();
			cout << r->data;
			r = r->rightchild;
		}
	}
}

3.二叉树的后序遍历

3.1递归算法

template<class temp>
void bintree<temp>::postorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		postorder(r->leftchild);
		postorder(r->rightchild);
		cout << r->data;
	}
}

3.2非递归算法

栈顶元素永远为当前元素的父节点，设r为当前访问的节点，则

1.若r！=NULL，r入栈（s[++top].r=r;），调用r=r->leftchild;将r标记为1（s[top].tag=1;），返回1；

2.若r==NULL，重新设r为栈顶元素

        2.1若r标记为2，说明右子树返回；访问r（cout<<s[top].r->data;）r出栈，重新设r为栈顶元素（top--；），返回2.1；

        2.2若r标记为1，说明左子树返回；调用r=r->rightchild；将r标记为2（s[top].tag=2;），返回1；

反复执行，直到栈空（top==-1），程序结束。

if(r!=NULL)

{

        入栈；

}

if(r==NULL)

        1:不出栈，换右支；

        2:cout<<r->data;出栈

template<class temp>
void bintree<temp>::stackpostorder(binnode<temp>* r)
{
	linkstack<temp> s[100];
	int top = -1;
	do
	{
		while (r != NULL)
		{
			s[++top].r = r;
			s[top].tag = 1;
			r = r->leftchild;
		}
		while ((top != -1) && (s[top].tag == 2))
		{
			cout << s[top].r->data;
			top--;
		}
		if ((top != -1) && (s[top].tag == 1))
		{
			r = s[top].r->rightchild;
			s[top].tag = 2;
		}
	} while (top != -1);
}

3.3说明

        非递归遍历的优化算法核心是：因为根节点的作用是索引左子树，所以访问完左子树之后根节点就没有意义了，所以可以跳过根节点直接访问右子树，从而减小了时间复杂度。但是在后序遍历中，根节点最后访问，所以没有相应的优化算法。

4.层序遍历

层序遍历请看这篇文章  有详细讲解~

北邮22信通：二叉树层序遍历的两种方法&&首发模板类交互_青山如墨雨如画的博客-CSDN博客

5.模板类实现栈完整代码

下面给出模板类实现栈的完整代码。

5.1代码部分

#include<iostream>
using namespace std;
#define MAXSIZE 100005

class student
{
private:
	int ID;
	string name;
public:
	int existence;
	student()
	{
		this->ID = 0;
		this->name = "unknown name";
		this->existence = 0;
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
		this->existence = 1;
	}
	friend ostream& operator<<(ostream& output, student& s)
	{
		output << s.ID << " " << s.name << endl;
		return output;
	}
};

template<class temp>
struct binnode;
//栈
template <class temp>
struct node
{
	temp data;
	node<temp>* next;
};

template <class temp>
class linkstack
{
public:
	binnode<temp>* r;
	int tag;
	linkstack() { top = NULL; }
	~linkstack();
	void push(temp x);
	temp pop();
	temp gettop();
	bool empty()
	{
		return top == NULL ? true : false;
	}
private:
	node<temp>* top;
};

template <class temp>
void linkstack<temp>::push(temp x)
{
	node<temp>* p = new node<temp>;
	p->data = x;
	p->next = this->top;
	this->top = p;
}

template<class temp>
temp linkstack<temp>::pop()
{
	if (empty())throw "下溢";
	temp x = this->top->data;
	node<temp>* p = this->top;
	this->top = this->top->next;
	delete p;
	return x;
}

template<class temp>
linkstack<temp>::~linkstack()
{
	while (this->top != NULL)
	{
		node<temp>* p = this->top;
		this->top = this->top->next;
		delete p;
	}
}

template<class temp>
temp linkstack<temp>::gettop()
{
	if (empty())throw"下溢";
	return this->top->data;
}

//二叉树
template<class temp>
struct binnode
{
	temp data;
	binnode<temp>* leftchild;
	binnode<temp>* rightchild;
};

template<class temp>
class bintree
{
private:
	void create(binnode<temp>*& r, temp data[], int i, int n);
	void release(binnode<temp>* r);
public:
	binnode<temp>* root;
	bintree(temp data[], int n);
	void preorder(binnode<temp>* r);
	void stackpreorder(binnode<temp>* r);
	void quickstackpreorder(binnode<temp>* r);
	void inorder(binnode<temp>* r);
	void stackinorder(binnode<temp>* r);
	void quickstackinorder(binnode<temp>* r);
	void postorder(binnode<temp>* r);
	void stackpostorder(binnode<temp>* r);
	void levelorder(binnode<temp>* r);

	~bintree();
};

template<class temp>
void bintree<temp>::create(binnode<temp>*& r, temp data[], int i, int n)
{
	if (i <= n && data[i - 1].existence != 0)
	{
		r = new binnode<temp>;
		r->data = data[i - 1];
		r->leftchild = r->rightchild = NULL;
		create(r->leftchild, data, 2 * i, n);
		/*书上代码错误1：向函数传入实参时少传入一个n*/
		create(r->rightchild, data, 2 * i + 1, n);/*书上代码错误同上*/
	}
}

template<class temp>
bintree<temp>::bintree(temp data[], int n)
{
	create(this->root, data, 1, n);
}

template<class temp>
void bintree<temp>::preorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		cout << r->data;
		preorder(r->leftchild);
		preorder(r->rightchild);
	}
}

template<class temp>
void bintree<temp>::stackpreorder(binnode<temp>* r)
{
	linkstack<temp> s[100];
	int top = -1;
	do
	{
		while (r != NULL)
		{
			s[++top].r = r;
			s[top].tag = 1;
			cout << s[top].r->data;
			r = r->leftchild;
		}
		while ((top != -1) && s[top].tag == 2)
			top--;
		if ((top != -1) && (s[top].tag == 1))
		{
			r = s[top].r->rightchild;
			s[top].tag = 2;
		}
	} while (top != -1);
}

template<class temp>
void bintree<temp>::quickstackpreorder(binnode<temp>* r)
{
	linkstack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			cout << r->data;
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.pop();
			r = r->rightchild;
		}
	}
}

template<class temp>
void bintree<temp>::inorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		inorder(r->leftchild);
		cout << r->data;
		inorder(r->rightchild);
	}
}

template<class temp>
void bintree<temp>::stackinorder(binnode<temp>* r)
{
	linkstack<temp> s[100];
	int top = -1;
	do
	{
		while (r != NULL)
		{
			s[++top].r = r;
			s[top].tag = 1;
			r = r->leftchild;
		}
		while ((top != -1) && (s[top].tag == 2))
			top--;
		if ((top != -1) && (s[top].tag == 1))
		{
			r = s[top].r->rightchild;
			cout << s[top].r->data;
			s[top].tag = 2;
		}
	} while (top != -1);
}

template<class temp>
void bintree<temp>::quickstackinorder(binnode<temp>* r)
{
	linkstack<binnode<temp>*>s;
	while (!s.empty() || r != NULL)
	{
		if (r != NULL)
		{
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.pop();
			cout << r->data;
			r = r->rightchild;
		}
	}
}

template<class temp>
void bintree<temp>::postorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		postorder(r->leftchild);
		postorder(r->rightchild);
		cout << r->data;
	}
}

template<class temp>
void bintree<temp>::stackpostorder(binnode<temp>* r)
{
	linkstack<temp> s[100];
	int top = -1;
	do
	{
		while (r != NULL)
		{
			s[++top].r = r;
			s[top].tag = 1;
			r = r->leftchild;
		}
		while ((top != -1) && (s[top].tag == 2))
		{
			cout << s[top].r->data;
			top--;
		}
		if ((top != -1) && (s[top].tag == 1))
		{
			r = s[top].r->rightchild;
			s[top].tag = 2;
		}
	} while (top != -1);
}

template<class temp>
void bintree<temp>::levelorder(binnode<temp>* R)
{
	binnode<temp>* queue[MAXSIZE];
	int f = 0, r = 0;
	if (R != NULL)
		queue[++r] = R;//根节点入队
	while (f != r)
	{
		binnode<temp>* p = queue[++f];//队头元素入队
		cout << p->data;//出队打印
		if (p->leftchild != NULL)
			queue[++r] = p->leftchild;//左孩子入队
		if (p->rightchild != NULL)
			queue[++r] = p->rightchild;//右孩子入队
	}
}

template <class temp>
void bintree<temp>::release(binnode<temp>* r)
{
	if (r != NULL)
	{
		release(r->leftchild);
		release(r->rightchild);
		delete r;
	}
}

template<class temp>
bintree<temp>::~bintree()
{
	release(this->root);
}

int main()
{

	system("color 0A");
	student stu[5] = { {1,"zhang"},{2,"wang"},{3,"li"},{4,"zhao"},{5,"liu"} };
	bintree<student>bintreee(stu, 5);
	cout << "前序遍历:" << endl;
	bintreee.preorder(bintreee.root);
	cout << endl << "模板类实现栈前序遍历:" << endl;
	bintreee.stackpreorder(bintreee.root);
	cout << endl << "栈快排前序遍历:" << endl;
	bintreee.quickstackpreorder(bintreee.root);

	cout << endl << "中序遍历:" << endl;
	bintreee.inorder(bintreee.root);
	cout << endl << "模板类实现栈中序遍历:" << endl;
	bintreee.stackinorder(bintreee.root);
	cout << endl << "栈快排中序遍历" << endl;
	bintreee.quickstackinorder(bintreee.root);

	cout << endl << "后序遍历:" << endl;
	bintreee.postorder(bintreee.root);
	cout << endl << "模板类实现栈后序遍历:" << endl;
	bintreee.stackpostorder(bintreee.root);

	cout << endl << "层序遍历:" << endl;
	bintreee.levelorder(bintreee.root);
	cout << endl;
	return 0;
}

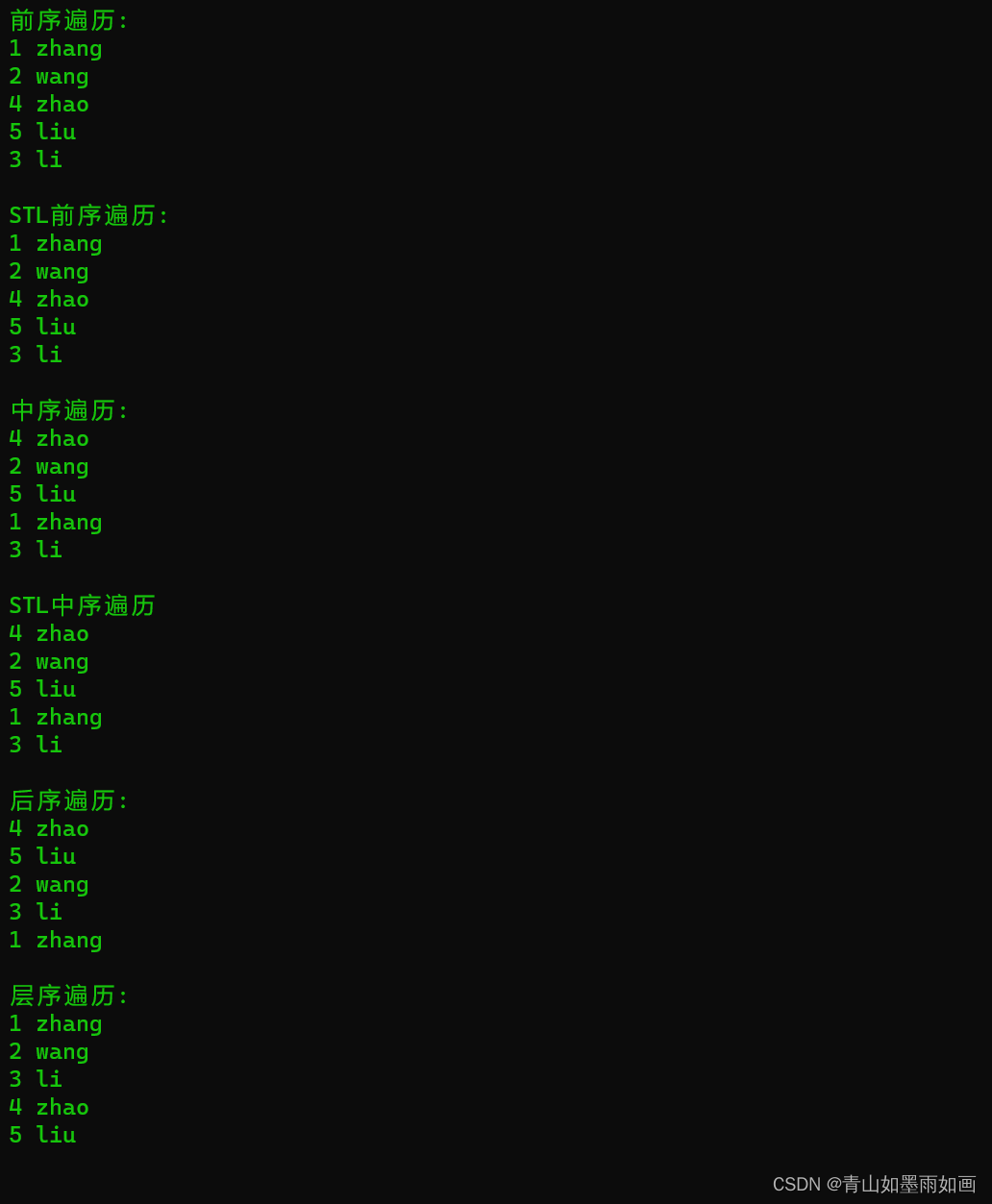
5.2运行结果

5.2.1代码效果图：

 5.2.2运行结果：

​

 6.STL实现栈完整代码

6.1代码部分

#include<iostream>
#include<stack>
using namespace std;
#define MAXSIZE 100005

class student
{
private:
	int ID;
	string name;
public:
	int existence;
	student()
	{
		this->ID = 0;
		this->name = "unknown name";
		this->existence = 0;
	}
	student(int ID, string name)
	{
		this->ID = ID;
		this->name = name;
		this->existence = 1;
	}
	friend ostream& operator<<(ostream& output, student& s)
	{
		output << s.ID << " " << s.name << endl;
		return output;
	}
};

//二叉树
template<class temp>
struct binnode
{
	temp data;
	binnode<temp>* leftchild;
	binnode<temp>* rightchild;
};

template<class temp>
class bintree
{
private:
	void create(binnode<temp>*& r, temp data[], int i, int n);
	void release(binnode<temp>* r);
public:
	binnode<temp>* root;
	bintree(temp data[], int n);
	void preorder(binnode<temp>* r);
	void quickSTLpreorder(binnode<temp>* r);
	void inorder(binnode<temp>* r);
	void quickSTLinorder(binnode<temp>* r);
	void postorder(binnode<temp>* r);
	void levelorder(binnode<temp>* r);

	~bintree();
};

template<class temp>
void bintree<temp>::create(binnode<temp>*& r, temp data[], int i, int n)
{
	if (i <= n && data[i - 1].existence != 0)
	{
		r = new binnode<temp>;
		r->data = data[i - 1];
		r->leftchild = r->rightchild = NULL;
		create(r->leftchild, data, 2 * i, n);
		/*书上代码错误1：向函数传入实参时少传入一个n*/
		create(r->rightchild, data, 2 * i + 1, n);/*书上代码错误同上*/
	}
}

template<class temp>
bintree<temp>::bintree(temp data[], int n)
{
	create(this->root, data, 1, n);
}

template<class temp>
void bintree<temp>::preorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		cout << r->data;
		preorder(r->leftchild);
		preorder(r->rightchild);
	}
}

template<class temp>
void bintree<temp>::quickSTLpreorder(binnode<temp>* r)
{
	stack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			cout << r->data;
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.top();
			s.pop();
			r = r->rightchild;
		}
	}
}

template<class temp>
void bintree<temp>::inorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		inorder(r->leftchild);
		cout << r->data;
		inorder(r->rightchild);
	}
}

template<class temp>
void bintree<temp>::quickSTLinorder(binnode<temp>* r)
{
	stack<binnode<temp>*>s;
	while (!s.empty() || (r != NULL))
	{
		if (r != NULL)
		{
			s.push(r);
			r = r->leftchild;
		}
		else
		{
			r = s.top();
			s.pop();
			cout << r->data;
			r = r->rightchild;
		}
	}
}

template<class temp>
void bintree<temp>::postorder(binnode<temp>* r)
{
	if (r != NULL)
	{
		postorder(r->leftchild);
		postorder(r->rightchild);
		cout << r->data;
	}
}

template<class temp>
void bintree<temp>::levelorder(binnode<temp>* R)
{
	binnode<temp>* queue[MAXSIZE];
	int f = 0, r = 0;
	if (R != NULL)
		queue[++r] = R;//根节点入队
	while (f != r)
	{
		binnode<temp>* p = queue[++f];//队头元素入队
		cout << p->data;//出队打印
		if (p->leftchild != NULL)
			queue[++r] = p->leftchild;//左孩子入队
		if (p->rightchild != NULL)
			queue[++r] = p->rightchild;//右孩子入队
	}
}

template <class temp>
void bintree<temp>::release(binnode<temp>* r)
{
	if (r != NULL)
	{
		release(r->leftchild);
		release(r->rightchild);
		delete r;
	}
}

template<class temp>
bintree<temp>::~bintree()
{
	release(this->root);
}

int main()
{

	system("color 0A");
	student stu[5] = { {1,"zhang"},{2,"wang"},{3,"li"},{4,"zhao"},{5,"liu"} };
	bintree<student>bintreee(stu, 5);
	cout << "前序遍历:" << endl;
	bintreee.preorder(bintreee.root);
	cout << endl << "STL前序遍历:" << endl;
	bintreee.quickSTLpreorder(bintreee.root);

	cout << endl << "中序遍历:" << endl;
	bintreee.inorder(bintreee.root);
	cout << endl << "STL中序遍历" << endl;
	bintreee.quickSTLinorder(bintreee.root);

	cout << endl << "后序遍历:" << endl;
	bintreee.postorder(bintreee.root);

	cout << endl << "层序遍历:" << endl;
	bintreee.levelorder(bintreee.root);
	cout << endl;
	return 0;
}

6.2运行结果：