基于杂草优化算法的线性规划问题求解matlab程序

1 杂草算法简介
1.1 IWO定义
IWO是2006年由A. R. Mehrabian等提出的一种从自然界杂草进化原理演化而来的随机搜索算法，模仿杂草入侵的种子空间扩散、生长、繁殖和竞争性消亡的基本过程，具有很强的鲁棒性和自适应性。

IWO算法是一种高效的随机智能优化算法，以群体中优秀个体来指导种群的进化，以正态分布动态改变标准差的方式将由优秀个体产生的子代个体叠加在父代个体周围，再经过个体之间的竞争，得到最优个体。算法兼顾了群体的多样性和选择力度。

1.2 IWO搜索与性能
IWO相比其他的进化算法拥有更大的搜索空间和更好的性能。与GA相比，IWO算法简单，易于实现，不需要遗传操作算子，能简单有效地收敛问题的最优解，是一种强有力的智能优化工具。
1.3 IWO算法实现步骤
1.3.1 初始化种群
一定数据的杂草初始分布在搜索空间中，位置随机，个数根据实际情况调整；
1.3.2 子代繁殖
分布在整个搜索空间的父代，根据父代的适应值产生下一代种子，种子的个数由适应度值决定，适应值高的产生的种子多，低的个体产生种子数少。
1.3.3 空间扩散
子代个体按照一定规律分布在父代个体周围，分布位置规律满足正态分布（父代为轴线（均值），标准差随着代数不断变化）。
1.3.4 竞争淘汰
当一次繁殖的个体数超过种群数量的上限时，将子代和父代一起排序，适应值低的个体将被清除。

2 线性规划算例
2.1算例

2.2算例答案

3 杂草优化算法求解结果

1）迭代曲线

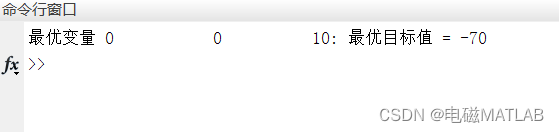
2）求解答案

4 matlab程序
1）主函数

%% 基于杂草算法的线性规划求解
clc;
clear;
close all;
%% Problem Definition
CostFunction = @(x) Sphere(x);     % 目标函数
nVar = 3;              % 决策变量数
VarSize = [1 nVar];    % 决策变量矩阵大小
VarMin = 0;       % 决策变量下限
VarMax = 15;        % 决策变量上限
%% IWO Parameters
MaxIt = 500;    % 最大迭代次数

nPop0 = 10;     % 初始种群规模
nPop = 25;      % 最大种群规模

Smin = 0;       % 繁殖种子数下限
Smax = 5;       % 繁殖种子数上限

Exponent = 3;             % 方差缩减指数（非线性调和因子）
sigma_initial = 0.5;      % 标准差初值
sigma_final = 0.001;	  % 标准差终值
%% Initialization
% 置空植物矩阵（包含位置和适应度值）
empty_plant.Position = [];
empty_plant.Cost = [];
pop = repmat(empty_plant, nPop0, 1);    % 初始种群矩阵
for i = 1:numel(pop)
    % 初始化位置
    pop(i).Position = unifrnd(VarMin, VarMax, VarSize);
    % 初始化适应度值
    pop(i).Cost = CostFunction(pop(i).Position);
end
% 初始化最优函数值历史记录
BestCosts = zeros(MaxIt, 1);
%% IWO Main Loop
for it = 1:MaxIt
    % 更新标准偏差
    sigma = ((MaxIt - it)/(MaxIt - 1))^Exponent * (sigma_initial - sigma_final) + sigma_final;
    % 获得最佳和最差的目标值
    Costs = [pop.Cost];
    BestCost = min(Costs);
    WorstCost = max(Costs);
    % 初始化子代种群
    newpop = [];
    % 繁殖
    for i = 1:numel(pop)
        % 比例系数
        ratio = (pop(i).Cost - WorstCost)/(BestCost - WorstCost);
        % 每个杂草产生的种子数
        S = floor(Smin + (Smax - Smin)*ratio);
        for j = 1:S
            % 初始化子代
            newsol = empty_plant;         
            % 生成随机位置
            % randn是一种产生标准正态分布的随机数或矩阵的函数
            newsol.Position = pop(i).Position + sigma * randn(VarSize); 
            % 边界(下限/上限)处理
            newsol.Position = max(newsol.Position, VarMin);
            newsol.Position = min(newsol.Position, VarMax);
            % 子代的目标函数值
            newsol.Cost = CostFunction(newsol.Position);
            % 添加子代
            newpop = [newpop;
                      newsol];  % #ok
        end
    end
    % 合并种群
    pop = [pop;
           newpop];
    % 种群排序
    [~, SortOrder] = sort([pop.Cost]);
    pop = pop(SortOrder);
    % 竞争排除（删除额外成员）
    if numel(pop)>nPop
        pop = pop(1:nPop);
    end
    % 保存最佳种群
    BestSol = pop(1);
    % 保存最优函数值历史记录
    BestCosts(it) = BestSol.Cost;
    % 显示迭代信息
%     disp(['Iteration ' num2str(it) ': Best Cost = ' num2str(BestCosts(it))]);
end
%% Results
figure;
% plot(BestCosts, 'LineWidth', 2);
semilogy(BestCosts, 'r', 'LineWidth', 2);
xlabel('Iteration');
ylabel('Best Cost');
grid on;
%% 输出结果
disp(['最优变量 ' num2str(BestSol.Position) ': 最优目标值 = ' num2str(BestCosts(it))]);

。。。。。。。略