最近实验中用到了仿射加解密算法，其中的解密操作是通过扩展欧几里得算法实现的，因此在这里对 欧几里得算法、扩展欧几里得算法 做一个完整的记录。

1. 欧几里得算法（也叫辗转相除法）

---

1.1 直接上模拟

现在求 6 和 16 的最大公约数，根据高中知识（其实我也忘了，现学的芭芭拉迪）：
每一次将除式中的除数作为下一次的被除数，将余数作为下一次的除数，直到商为 0，此时的除数就是最大公约数：

• 16 ➗ 6 = 2 $\cdots \cdots$ 4
• 6 ➗ 4 = 1 $\cdots \cdots$ 2
• 4 ➗ 2 = 2 $\cdots \cdots$ 0

因此，最大公约数为 2；

---

1.2 几何理解

假设现在需要对 a, b (不妨假设 a >b) 求最大公约数，在几何上可以这样进行理解：

• 以 $a,b$ 为矩形的边长，构造一个矩形 $A$；
• 以矩形的短边（这里为 $b$）构造正方形 B，然后计算这样的正方形 B 在矩形 A 中最多能够放置多少个；

这样就对问题进行了一个抽象：目标就是去寻找能够没有缝隙地铺满矩形 $A$ 的正方形 $B$ 的最大边长值；
假设上面的正方形 $B$ 不能将矩形 $A$ 铺满，那么接下来：

• 用长边剩余的长度够构建正方形，继续去填补未被覆盖的部分；
• 以此类推，直到找到一个能够刚好无缝隙地填满未覆盖部分的正方形，这个正方形的边长就是最大公约数；

这样会产生一个疑问，怎么保证填满未覆盖部分的正方形能够填满大的矩形呢？
我们通过作图来理解：

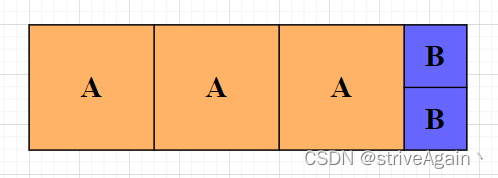
可以看到正方形 $B$ 刚好填满了正方形 $A$ 未覆盖的部分，并且显然从最右边的 $A$ 与两个 $B$ 的关系可以看出 $A$ 的边长是 $B$ 的两倍。
那么，如果用 $B$ 来填充 $A$ 的话，

• 纵向可以刚好填满，
• 而又因为 $A$ 是正方形，因此横向也可以刚好填满，

这就证明了：能填满未覆盖部分的 $B$ 一定可以填满覆盖了的所有 $A$，这就是欧几里得算法的几何解释；
现在用函数 $gcd(b,a)$ 来表示在长边为 $a$，短边为 $b$ 的矩形中，刚好能够无缝隙地覆盖的最大正方形边长，那么有

• 长边剩余部分的长度为 $a\%b$；
• 短边为 $b$；
• 上述几何解释告诉我们：$gcd(a,b)=gcd(b,a\%b)$；

---

1.3 用代数方法证明 $gcd(a,b)=gcd(b,a\%b)$

1.3.1 左推右：$gcd(a,b)=gcd(b,a\%b)$

现在有一个除式：$A➗B=C\cdots \cdots D$，并且 $A$ 和 $B$ 的最大公约数为 $k$，现在要求 $k$：

• 由题可设：$A=a\times k，B=b\times k$；
• 又因为 $D=A-B\times C$；
• 所以 $D=k(a-b\times C)$；
• 由于 $a,b,C,k$ 都是整数，因此 $D$ 也是整数，且是 $k$ 的倍数；
• 所以，被除数、除数、余数都有相同的公约数 $k$，且一定是最大的（假设不是最大的，则这个数一定也是被除数和除数的公约数，这与假设中的 最大公约数 矛盾）

因此，左推右得证；

1.3.2 右推左：$gcd(b,a\%b)=gcd(a,b)$

这个跟左推右的证明思路一样，关于除式 $A➗B=C\cdots \cdots D$，假设 $B$ 和 $D$ 的最大公约数为 $m$，现在要求 $m$：

• 由题可设：$B=b\times m,D=d\times m$；
• 又因为 $A=B\times C+D$；
• 所以 $A=m(bC+d)$；
• 由于 $b,C,d,m$ 都是整数，因此 $A$ 也是整数，且是 $m$ 的倍数；

因此，右推左得证；

---

1.4 欧几里得算法（辗转相除法）代码

展开版：

int gcd(int a, int b) {
	if (!b) {
		return a;
	}
	
	return gcd(b, a % b);
}

简化版：

int gcd(int a, int b) {
    return (b) ? gcd(b, a % b) : a;
}

---

2. 扩展欧几里得算法

扩展欧几里得算法是在欧几里得算法的运行过程中，求出方程 $ax+by=c$ 的一组解的算法；

2.1 直接上模拟

对于上面我们对欧几里得算法进行的模拟过程：

• 16 ➗ 6 = 2 $\cdots \cdots$ 4
• 6 ➗ 4 = 1 $\cdots \cdots$ 2
• 4 ➗ 2 = 2 $\cdots \cdots$ 0

可以从下到上对这些式子进行变形：

• $2=4\times 0+2\times 1$
• $2=6\times 1+4\times (-1)$
• $2=16\times (-1)+6\times 3$

意思就是说，一定可以找到方程 $gcd(a,b)=ax+by$ 的一组解；

---

2.2 裴蜀定理

由上面的分析可以得到一个定理：
裴蜀定理：设 a, b 为正整数，则关于 x, y 的方程 ax + by = c 有整数解 当且仅当 c 是 gcd(a, b) 的倍数;
下面给出一个简要的证明：
$$\begin{array}{rl}& \because ax+by=c\\ & \therefore \frac{a}{gcd(a,b)}x+\frac{b}{gcd(a,b)}y=\frac{c}{gcd(a,b)}\\ & \because gcd(a,b)肯定是a,b的因子\\ & \therefore 等式左边肯定是一个整数\\ & \therefore 等式右边也是整数\\ & \therefore 不妨设k=\frac{c}{gcd(a,b)}\\ & \therefore c=k\cdot gcd(a,b)\\ & \therefore c是gcd(a,b)的倍数\end{array}$$
充分性按照上面的思路反推即可；
因此，假设现在要求 $ax+by=c=k\cdot gcd(a,b)$ 的一组解，只需求出 $ax+by=gcd(a,b)$ 的一组解 $(x^{\prime },y^{\prime })$，然后令系数 $x=k{x}^{\prime },y=k{y}^{\prime }$ 即可；

---

2.3 算法公式推导

现在看下面的方程：
$$b{x}_0+(a\%b)y_0=gcd(b,a\%b)$$
由于 $gcd(a,b)=gcd(b,a\%b)$，因此有
$$b{x}_0+(a\%b)y_0=gcd(a,b)$$
因此有
$$b{x}_0+(a-\lfloor \frac{a}{b}\rfloor \times b)y_0=gcd(a,b)$$
整理得到
$$a{y}_0+b(x_0-\lfloor \frac{a}{b}\rfloor y_0)=gcd(a,b)$$
由于 $ax+by=gcd(a,b)$，对比两个方程，令对应系数相等可以得到：
$$\{\begin{array}{rl}& x=y_0\\ & y=x_0-\lfloor \frac{a}{b}\rfloor y_0\end{array}$$
所以递归更新参数 $x,y$，即可得到答案；

---

下面看看递归终止条件是什么：
当 $b=0$ 时有：
$$gcd(a,b)=a$$
此时对于方程 $ax+by=gcd(a,b)$，有
$$x=1,y=0$$
此为递归终止条件；

2.4 上代码

// d 为最大公约数
int extgcd(int a, int b, int& x, int& y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }

    int d = extgcd(b, a % b, x, y);
    int x0 = x, y0 = y;

    x = y0;
    y = x0 - (a / b) * y0;

    return d;
}

简化版还可以在递归的时候交换一下 $y$ 和 $x$：

int extgcd(int a, int b, int& x, int& y) {
    if (!b) {
        x = 1;
        y = 0;
        return a;
    }

    int d = extgcd(b, a % b, y, x);
    y -= (a / b) * x;

    return d;
}

---

2.5 扩展欧几里得算法的应用

2.5.1 应用一：求解不定方程

这个过程就是求 $ax+by=c$ 的一组整数解，上面已经进行了模拟；

2.5.2 应用二：求乘法逆元

首先给出乘法逆元的定义：

若 $a$ 与 $p$ 互质，则满足 $(a\times x)modp=1$ 的 $x$ 为 $a$ 在该条件下的逆元；

举个例子：求 7 模 11 的逆元，由于 $7\times 8=5\times 11+1$，因此有 $(7\times 8)mod11=1$，因此 7 在该条件下的逆元为 8；

因此，现在给出 $a$ 和 $p$，求出的方程 $ax+kp=1$ 的一组解 $(x_1,k_1)$ 其中的 $x_1$ 就是 $a$ 在该条件下的逆元；

要使用扩展欧几里得算法进行求解，需要满足 $gcd(a,p)=1$，即 $a$ 与 $p$ 互质，一定注意这个条件！！！

---

2.6 拓展：扩展欧几里得算法的通解

上面的过程我们只是求出了方程 $ax+by=c$ 的一组特解，现在要求的是其通解，可参考下面的过程：

2.6.1 $\frac{a}{gcd(a,b)}$ 与 $\frac{b}{gcd(a,b)}$ 互质

首先证明 $\frac{a}{gcd(a,b)}$ 与 $\frac{b}{gcd(a,b)}$ 互质：

采用反证法
假设 $\frac{a}{gcd(a,b)}$ 与 $\frac{b}{gcd(a,b)}$ 不互质，说明它们之间还有不等于 1 的公约数
假设这个公约数为 $k(k>0且k\ne 1)$；
因此有 $\frac{a}{gcd(a,b)}=k\Rightarrow a=k\cdot gcd(a,b)>gcd(a,b)$；
这就违反了 gcd(a, b) 求取的是最大公约数的约定；
因此 $\frac{a}{gcd(a,b)}$ 与 $\frac{b}{gcd(a,b)}$ 互质；

2.6.2 求通解

$$\begin{array}{rl}假设(x,y)与& (x_0,y_0)都是方程ax+by=c的解，因此有：\\ & ax+by=c\cdots \cdots ①\\ & a{x}_0+b{y}_0=c\cdots \cdots ②\\ & ①-②，有：a(x-x_0)=b(y_0-y)\\ & 两边同时除以gcd(a,b)\\ & \frac{a}{gcd(a,b)}(x-x_0)=\frac{b}{gcd(a,b)}(y_0-y)\\ & \because \frac{a}{gcd(a,b)}与\frac{b}{gcd(a,b)}互质\\ & \therefore x-x_0=t\cdot \frac{b}{gcd(a,b)}\to x=x_0+t\cdot \frac{b}{gcd(a,b)}\\ & \therefore y_0-y=t\cdot \frac{a}{gcd(a,b)}\to y=y_0-t\cdot \frac{a}{gcd(a,b)}\end{array}$$

欢迎补充~