知识导图：

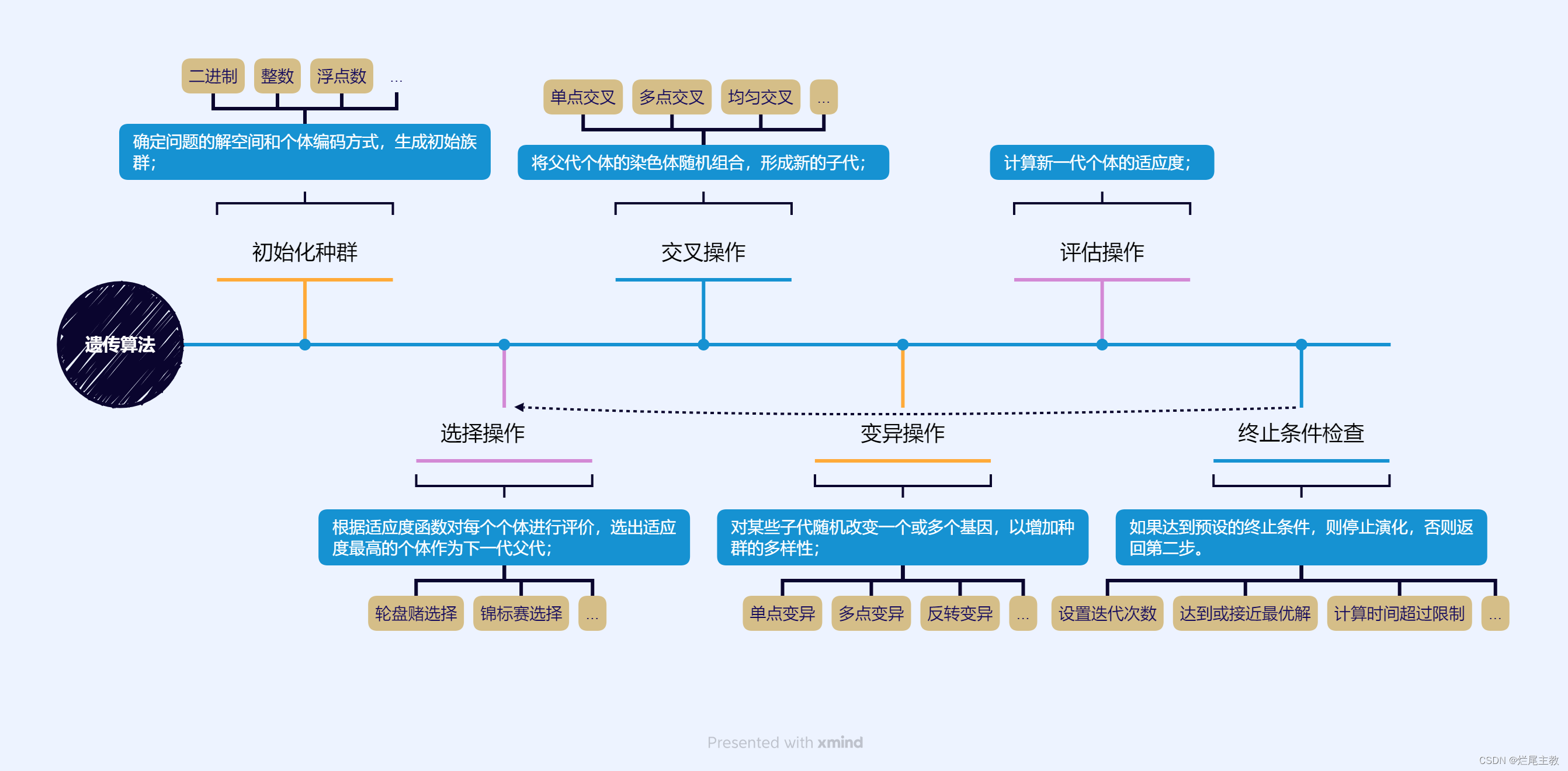
遗传算法（概念）

可以把遗传算法类比成一个游戏，我们需要通过这个游戏来找到最佳的解决方案。

首先，我们需要创建一些角色（也就是种群），每个角色有自己的装备和技能（染色体），但是我们并不知道哪个角色更加强大。
然后，我们让这些角色相互竞争，通过升级、打怪等方式来获得经验值（适应度值）。经验值越高的角色，就拥有了更多胜利的可能性。
接着，我们会将经验值高的角色进行复制，将装备/技能进行升级，继承属性（对应其交叉操作），而一些随机变异的角色也会加入其中。这些新的角色代表了我们在寻找答案的过程中的探索。如果它们的表现好于之前的角色，那么我们就可以用它们来代替原来的角色。
最后，通过这样的迭代过程，我们会逐渐找到最强大的角色，也就是最优解。

总之，遗传算法通过不断地试错，从而找到最优解决方案，就像在玩游戏一样。

具体来说，遗传算法的流程包括以下几个步骤：

初始化种群：通过随机方式生成一组初始解，称为种群。
适应度函数：根据问题要求，设计一个适应度函数，用于评价每个个体的好坏程度。
选择操作：按照适应度函数的评价结果，从当前种群中选择一些优秀的个体作为父代，并使用复制、交叉等方法产生下一代种群。
变异操作：在新产生的个体中进行随机变异的操作，增加搜索的多样性。
终止条件：根据预设的停止条件（如迭代次数、达到最优解等）决定算法何时结束。

遗传算法通过不断地试错，在种群中选择、交叉和变异来生成新的个体，并计算它们的适应度值。然后，根据设定的适应度函数来选择出适应度值高的个体作为下一代的父母，再进行交叉和变异操作，生成新的个体。通过这样的迭代过程，逐渐找到最优解决方案

1.初始化种群

初始化种群是指在遗传算法中，初始阶段按照其规定的编码方式随机生成一组个体，并将其作为遗传算法的起点。

这些个体构成了一个种群，每个个体都代表了问题的一个可能解。通过对这些个体进行交叉、变异等操作，不断迭代，从而逐步逼近问题的最优解。因此，初始化种群的质量和数量对于遗传算法的性能有很大影响。

基础篇，理解并学会使用以下三种编码方式方法：

二进制
整数
~~浮点数~~

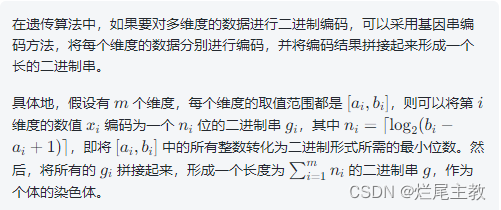
二进制编码与解码

顾名思义，就是将10进制数编码成二进制数

以下是我总结的常用方式和其代码：

假设需要解决一个最小化函数 $f (x)$ （适应函数 $f$ ），其中变量x是取值范围出现以下情况：

1. 当x是取值范围为 $[a, b]$ 之间的实数。公式(一)： $a+\frac{x_{⑩}}{2^n-1}*(b-a)$

例如：假设需要解决一个最小化函数f(x)，其中变量x是取值范围为[0,10]之间的实数。可以将x表示为一个长度为n的二进制串，其中n满足 $2^n-1>=10$ 。例如，当 $n = 5$ 时，可将二进制串 $10101$ 表示为 $(\frac{21}{31})*10=6.77$

$x_{⑩}$ 是二进制串的值（10进制），如10101的值为21

n的取值和你所需要的精度p有关， $2^{n-1}<(b-a)*10^p<2^{n}$

例如：例子来源

代码：

import math
import random


# 求n（已知精度p,x的取值范围[a,b]）
def calculate_n(p, a, b):
    power = math.log2((b - a) * 10 ** p)
    n = math.ceil(power)
    return n


# 随机生成n位二进制数
def generate_binary_number(n):
    binary = ""
    for i in range(n):
        bit = random.randint(0, 1)
        binary += str(bit)
    return binary


# 初始化种群（二进制版）
def initialize_population(population_size, n):
    population = []
    for i in range(population_size):
        individual = generate_binary_number(n)
        population.append(list(map(int,individual)))
    return population


n = calculate_n(1, -5, 5)
print(n)
population = initialize_population(100, n)
print(population)