刷题顺序参考于《2023华为机考刷题指南：八周机考速通车》

前言

单调栈：分为单调递增和单调递减栈。(栈内元素成递增或者递减性)：

单调递增栈：从栈底到栈顶数据是从大到小，即栈内的元素从栈顶到栈底是递增的，也就是栈顶的最小，栈底最大；
单调递减栈：从栈底到栈顶数据是从小到大，栈内的元素从栈顶到栈底是递减的，也就是栈顶的最大，栈底最小。

单调栈的性质：元素加入栈前会把栈顶破坏单调性的元素删除；一般使用单调栈的题目具有以下的两点：离自己最近（栈的后进先出的性质），比自己大（小）、高(低)；

单调栈的应用：单调栈一般是用来解决需要寻找当前点的左右边界最大最小值之类的问题；主要应用：

如果是求右边的第一个最大，那么就是从右向左遍历，构建单调递增栈；
如果是求右边的第一个最小，那么就是从右向左遍历，构建单调递减栈；
如果是求左边的第一个最大，那么就是从左向右遍历，构建单调递增栈；
如果是求左边的第一个最小，那么就是从左向右遍历，构建单调递减栈；

……
简言之：求第一个最大用单调递增栈，求第一个最小用单调递减栈，根据左右，选择是前向遍历还是后向遍历。

单调栈使用模板：

stack<Integer> stack = new Stack<>();
for (遍历这个数组){
   if (栈空 || 栈顶元素大于等于当前比较元素){
       入栈;
   }
   else{
       while (栈不为空 && 栈顶元素小于当前元素){
            栈顶元素出栈;
            更新结果;
        }
        当前数据入栈;
   }
}

更多内容可参考：
[1] 单调栈什么时候从后向前遍历，什么时候从前向后遍历？
[2] 刷题笔记6（浅谈单调栈）

一、739. 每日温度

1、题目描述

给定一个整数数组 temperatures ，表示每天的温度，返回一个数组 answer ，其中 answer[i] 是指对于第 i 天，下一个更高温度出现在几天后。如果气温在这之后都不会升高，请在该位置用 0 来代替。

2、测试用例

在这里插入图片描述

3、题解

根据题目分析，要求我们找出右边第一个最大，那么根据前言中的总结，就需要我们从右向左（倒序遍历）的构建单调递增栈。

3.1 单调栈（⭐）

时间复杂度 O(n) ，空间复杂度 O(n)

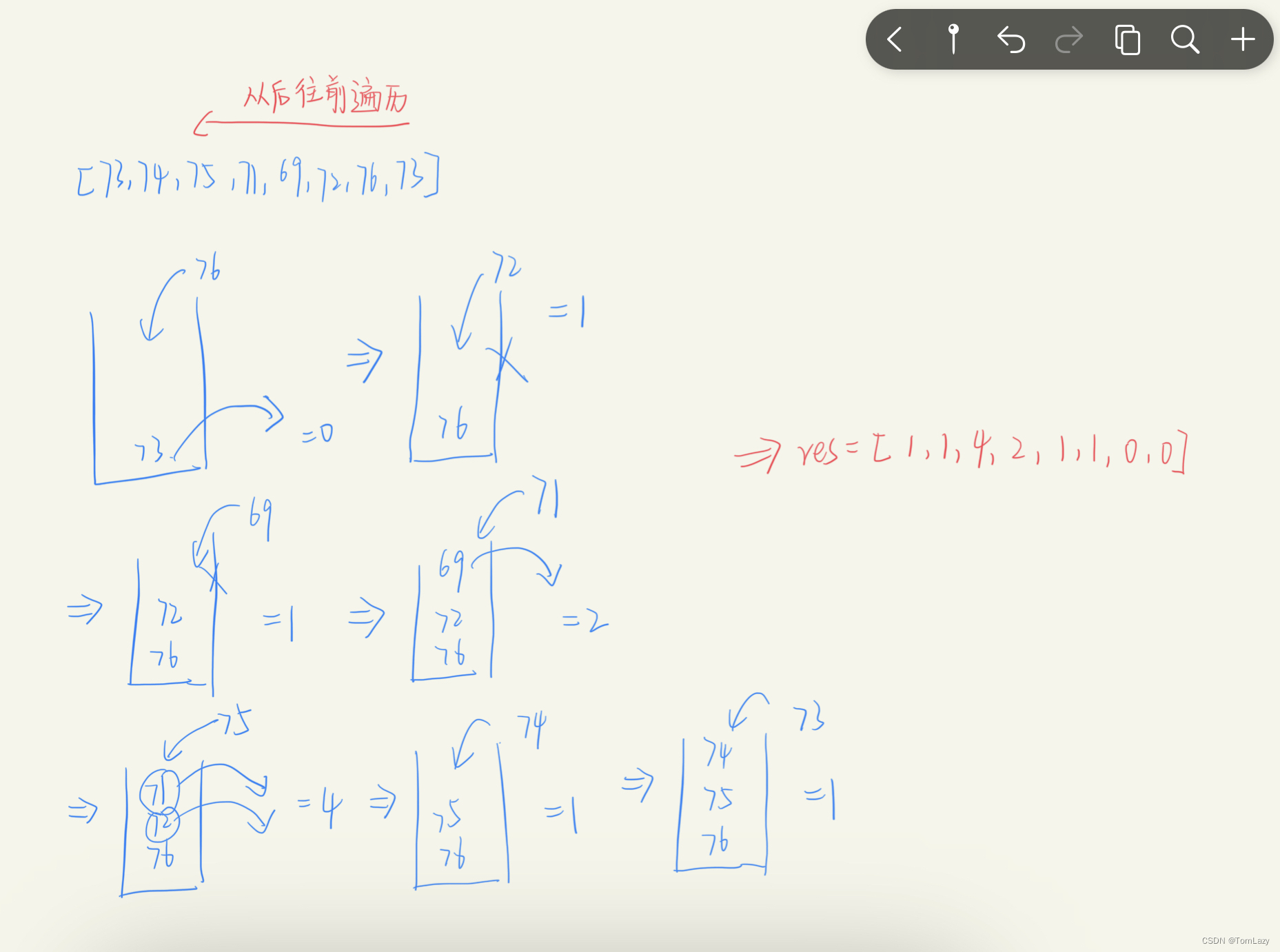
以 [73,74,75,71,69,72,76,73] 为例的单调栈过程：
在这里插入图片描述

class Solution {
    // 思路分析：
    // 1. 非最高温度 对应 下一个更高温度与当前温度的位置差
    // 2. 数组中当前最高 对应 0
    
    // 难点在于：
    // - 如何确定当前数 较之 后面的元素 是否为最大
    
    // Solution1：枚举思路：（遇事不决，暴力枚举！）
    // - 让每个元素都与其后面的元素作比较，直到找到比当前元素大的元素或结束
    // - 时间复杂度为 O(n^2)，超出时间限制
    
    // 如何进行优化，降低时间复杂度呢？
    // 枚举的高时间复杂度原因在于 对于每一个元素的最坏情况 都有可能是遍历完整个数组
    // 那么是否有办法很快就让当前元素 确定 下一个比它大的数呢？
    
    // Solution2：单调栈：从后往前遍历，既然从前往后遍历，我们在当前位置就确定谁大谁小（因为没遍历到后面的元素），
    // 那么我们就从后往前遍历，后面的遍历过了，当前的只需要判断就可以

    public int[] dailyTemperatures(int[] temperatures) {
        // 无效输入判断
        int n = temperatures.length;
        if (n <= 0) return new int[0];
        // 定义结果数组，用来返回结果，数组会默认初始化，数组元素全为0
        int[] res = new int[n];
        // 定义一个栈，用来实现单调栈，栈中元素保持 从 栈底到栈顶 数据是从大到小
        Stack<Integer> stack = new Stack<>();
        // 从后向前遍历
        for (int i = n-1; i >= 0; i--) {
            // 如果栈中元素非空，且当前元素大于栈顶元素，则说明后面没有比当天的气温高，弹出栈顶元素
            while (!stack.isEmpty() && temperatures[i] >= temperatures[stack.peek()]) 
                stack.pop();
            // 比较完毕后，如果此时栈为空的话，则说明后面没有比当天更高的温度，该天即为最高温度，赋值为 0
            // 如果栈不为空，则说明后面存在比当天更高的温度，那么让 此时的 栈顶元素 - i 即可
            res[i] = stack.isEmpty() ? 0 : stack.peek() - i;
            // 元素入栈
            stack.push(i);
        }
    
        // 循环结束，返回结果
        return res;
    }  
}

在这里插入图片描述

3.2 暴力枚举 (超时)

时间复杂度 O(n²) ，空间复杂度 O(n)

class Solution {
    // 枚举思路：
    // - 让每个元素都与其后面的元素作比较，直到找到比当前元素大的元素或结束
    public int[] dailyTemperatures(int[] temperatures) {
        // 无效输入判断
        if (temperatures.length <= 0) return new int[0];
        // 定义结果数组，用来返回结果，数组会默认初始化，数组元素全为0
        int[] res = new int[temperatures.length];
        // 双循环遍历
        for (int i = 0; i < temperatures.length-1; i++) {
            for (int j = i+1; j < temperatures.length; j++) {
                if (temperatures[i] < temperatures[j]) {
                    res[i] = j-i;
                    break;
                }
            }
        }
        // 循环结束，返回结果
        return res;
    }  
}

在这里插入图片描述

二、503. 下一个更大元素 II

1、题目描述

给定一个循环数组 nums （ nums[nums.length - 1] 的下一个元素是 nums[0] ），返回 nums 中每个元素的下一个更大元素。

数字 x 的下一个更大的元素是按数组遍历顺序，这个数字之后的第一个比它更大的数，这意味着你应该循环地搜索它的下一个更大的数。如果不存在，则输出 -1 。

2、测试用例

在这里插入图片描述

3、题解

与上一题 739 不同，该题给定的数组是一个循环数组，所以要考虑的更多，简单的说就是之前我们只考虑每个元素的后面就行了，现在循环数组的话他前面的元素也有可能成为它的下一个更大元素。

Note：循环数组的下标可以用取余的方式减少重复循环，达到直接定位的效果，如在本题中就通过了 i%n 的方式实现了对数组下标的定位，更多的相关内容可参考【LeetCode】剑指 Offer 62. 圆圈中最后剩下的数字（约瑟夫环问题） p300 – Java Version（模拟环形链表）。

3.1 两次遍历 + 单调栈（⭐）

时间复杂度 O(n) ，空间复杂度 O(n)
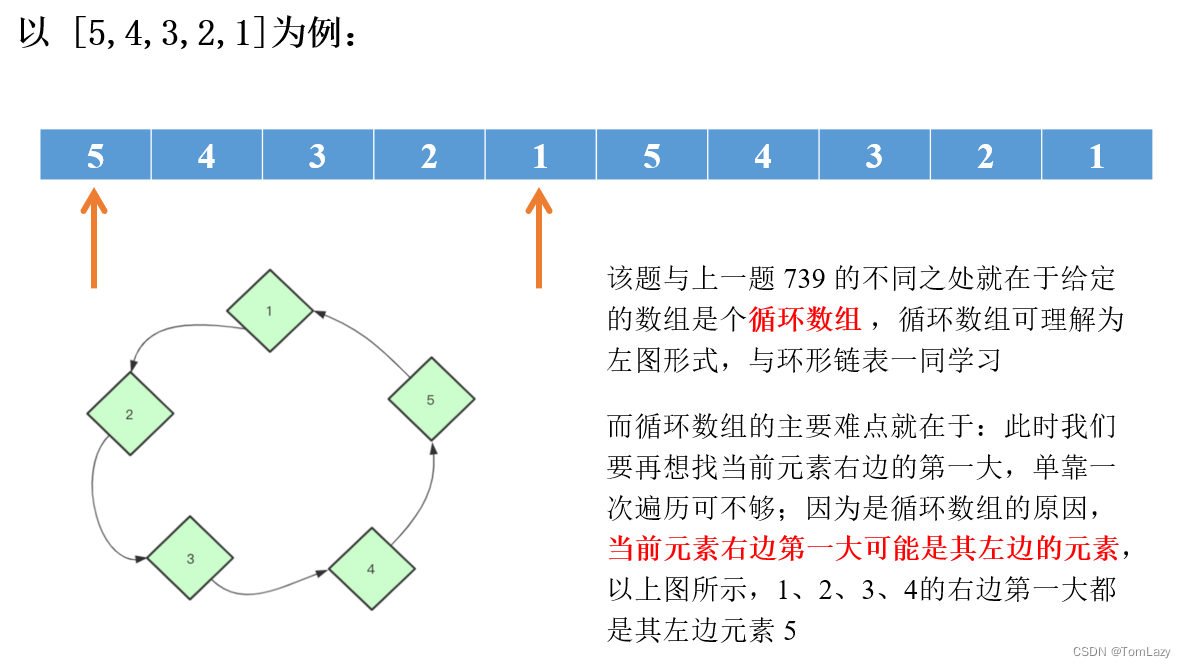
在这里插入图片描述

Q1：元素右边第一大可能是其左边的元素，那么是否可以通过单调栈找左第一大的方式找到该元素？
不能！与一开始的分析和上图可知，由于形参 nums 是一个循环数组，那么其中的某一元素的右边第一大就有可能是其左边的元素，那么我们该如何来解决这个问题呢？是要实现两个单调栈，一个去找右第一大，一个去找左第一大吗？非也！因为找左第一大，不符合题意，由于是循环数组的原因，1 的右第一大应该是 5，如果我们去找了 1 的左第一大，那么找到的结果是 2，很明显不符合题意。

Q1：元素右边第一大可能是其左边的元素，那么是否可以通过单调栈找左第一大的方式找到该元素？

不能！与一开始的分析和上图可知，由于形参 nums 是一个循环数组，那么其中的某一元素的右边第一大就有可能是其左边的元素，那么我们该如何来解决这个问题呢？是要实现两个单调栈，一个去找右第一大，一个去找左第一大吗？非也！因为找左第一大，不符合题意，由于是循环数组的原因，1 的右第一大应该是 5，如果我们去找了 1 的左第一大，那么找到的结果是 2，很明显不符合题意。

那么正确的做法就应该是：

将循环范围扩大到数组长度的 2 倍，通过索引 % 数组长度的这种求余方式来定位数组下标，这就相当于对数组进行了两次遍历，此时进行的单调栈中就包含了当前元素的左边元素（因为我们在遍历第一遍数组的时候，就已经将数组中最大的元素存入了栈中，所以第二次遍历的时候，如果当前元素它的右边第一大是它的某个左元素，那么这个左元素此时一定存储在了单调栈中）
直接定义一个二倍数组长度的临时数组，将入参数组 nums 中的元素拷贝两次，然后倒序实现单调递增栈即可，该题解写法可见 3.2

class Solution {
    // Solution1: 两次遍历 + 单调栈
    public int[] nextGreaterElements(int[] nums) {
        
        int n = nums.length; // 获得数组长度
        Stack<Integer> rs = new Stack<>();  // 倒序遍历 找 右第一大
        int[] res = new int[n]; // 定义返回数组，用来存储返回结果

        for (int i = 2*n-1; i >= 0; i--) // 倒序找右第一大，通过取余的方式相当于人工拼接了一次数组
        {
            while (!rs.isEmpty() && nums[i%n] >= nums[rs.peek()]) rs.pop();
            res[i%n] = rs.isEmpty() ? -1 : nums[rs.peek()]; // 定位右第一大元素是谁
            rs.push(i%n); // 将数组元素下标依次压栈
        }

        return res;
    }
}

在这里插入图片描述

3.2 double数组 + 单调栈

时间复杂度 O(n) ，空间复杂度 O(n)

class Solution {
    // Solution2: double数组 + 单调栈
    public int[] nextGreaterElements(int[] nums) {
        
        int n = nums.length; // 获得数组长度
        Stack<Integer> rs = new Stack<>();  // 倒序遍历 找 右第一大
        int[] res = new int[n]; // 定义返回数组，用来存储返回结果

        int[] tmp = new int[2*n]; // 拷贝两次输入数组
        for (int i = 0; i < 2*n; i++) 
        {
            tmp[i] = nums[i%n];
            //System.out.println(tmp[i]);
        }
        
        for (int i = 2*n-1; i >= 0; i--) // 倒序找右第一大
        {
            while (!rs.isEmpty() && tmp[i] >= tmp[rs.peek()]) rs.pop();
            res[i%n] = rs.isEmpty() ? -1 : tmp[rs.peek()]; // 定位右第一大元素是谁
            rs.push(i); // 将数组元素下标依次压栈
        }

        return res;
    }
}

在这里插入图片描述

三、901. 股票价格跨度

1、题目描述

设计一个算法收集某些股票的每日报价，并返回该股票当日价格的跨度。
当日股票价格的跨度被定义为股票价格小于或等于今天价格的最大连续日数（从今天开始往回数，包括今天）。

例如，如果未来 7 天股票的价格是 [100,80,60,70,60,75,85]，那么股票跨度将是 [1,1,1,2,1,4,6] 。

在这里插入图片描述

2、测试用例

在这里插入图片描述

3、题解

该题与前两题不同之处在于：前两题都是找右第一大，本题是来找左第一大，所以根据前言中的模板，此时我们需要从左到右的去构建一个从栈顶到栈底单调递增栈，通过这种方式，我们就可以从左向右遍历所有元素，如果遍历到的当前元素 大于等于 栈顶元素，则弹出栈顶元素，直至栈中出现了比当前元素大的数，才停止弹出，此时用当前遍历元素的下标减去栈顶元素的下标即为今日股票价格的跨度。

3.1 单调栈 + 二元对（⭐）

时间复杂度 O(n) ，空间复杂度 O(n)
以 [100,80,60,70,60,75] 为例的出出入栈过程，如下图所示：
在这里插入图片描述

由于本题中没有给定类似数组之类的输入参数，而是需要我们自己去补充完成 next 方法，所以我们没有办法直接获取到输入数据的下标，那么此时就需要我们从 0 开始定义它的下标 idx，并将其同价格一同存储起来，我们可以使用二元数对 int[2] 来存储股票价格的下标（即天数）和股票价格（其中，int[0] 为当前股票价格下标，int[1]为当前股票价格）。同时，我们可以在栈中先插入一个最大值作为天数为 −1 天的价格，来保证栈不会为空。调用 next 时，时，先将栈中价格小于等于此时 price 的元素都弹出，直到遇到一个大于 price 的值，并将 price 入栈，计算下标差后返回。

class StockSpanner {
    Stack<int[]> stack;
    int idx;

    public StockSpanner() {  // 构造函数：用来初始化定义的数据结构
        stack = new Stack<int[]>();  
        stack.push(new int[]{-1, Integer.MAX_VALUE});
        idx = -1;
    }

    public int next(int price) {    
        idx++;
        while (price >= stack.peek()[1]) {  // 二元对：[0]代表下标索引，[1]代表价格
            stack.pop();
        }
        int ret = idx - stack.peek()[0];  // 下标差
        stack.push(new int[]{idx, price});
        return ret;
    }
}
/**
 * Your StockSpanner object will be instantiated and called as such:
 * StockSpanner obj = new StockSpanner();
 * int param_1 = obj.next(price);
 */

在这里插入图片描述

3.2 单调栈 + 哈希表

如果不使用下标索引呢，那么该题就需要在遍历的过程中进行累加操作了，因为我们是从左向右遍历得出每个元素到其左第一大元素之间的跨度，那么当前元素的跨度，就会栈顶元素与它的左第一大元素之间产生了关系（如果当前元素比栈顶元素大，那么也就说明，当前栈顶元素到其左第一大元素之间的跨度属于当前元素中的一部分，然后再比较当前元素与栈顶元素的左第一大元素，如果还是当前元素要大，那么就继续比较下一个左第一大元素，直至找到比当前元素大的元素为止）

当然，即使不使用下标索引，我们还是需要一个二元数对来保存两个元素，一个是当前的股票价格，另一个就是要返回的结果：股票的跨度；那么除了用数组来存储，我们也可以使用哈希表（k-v） 来进行存储，让 key 为股票价格，value 为跨度。

Note：这里还有一个小的注意点，要注意 map.put(price,count) 的位置，不要将其写在循环里面，因为如果入参中存在重复元素时，map.get(stack.peek()) 时就有可能获得到之前存在的，然而新存在的又会覆盖掉之前的，累加起来就会导致结果错误。

class StockSpanner {
    HashMap<Integer,Integer> map;
    Stack<Integer> stack;
    
    public StockSpanner() {
        map=new HashMap<>();
        stack=new Stack<>();
        stack.push(Integer.MAX_VALUE); // 哨兵 永远在栈中 
    }
    
    public int next(int price) {
        int count = 1;
        while(price >= stack.peek()){
            count += map.get(stack.peek());
            stack.pop();
        }
        stack.push(price);
        map.put(price,count);
        return count;
    }
}

在这里插入图片描述

3.3 其它方法（两个栈/数组指针）

两个栈方法可参考：股票价格跨度 – LeetCode
数组+指针方法可参考：【爪哇缪斯】图解LeetCode

四、84. 柱状图中最大的矩形

1、题目描述

给定 n 个非负整数，用来表示柱状图中各个柱子的高度。每个柱子彼此相邻，且宽度为 1 。

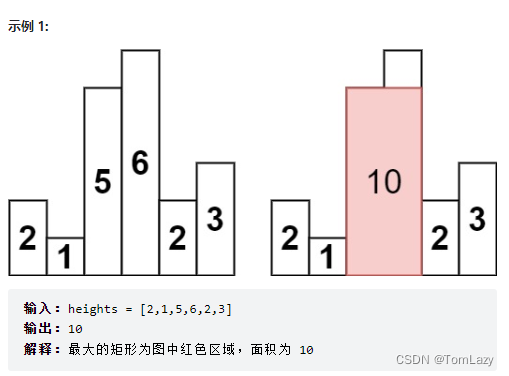
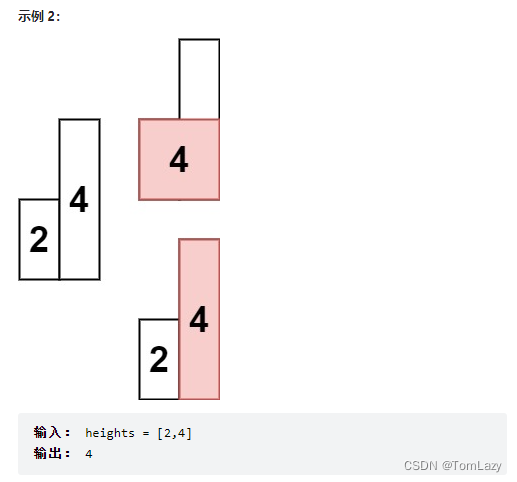
求在该柱状图中，能够勾勒出来的矩形的最大面积。

2、测试用例

在这里插入图片描述

3、题解

笔试面试高频题。该题也可理解成找左边第一小，但找左边第一小只是为了确定左边界，还需经过面积公式的操作求出柱形图中可能的矩阵的最大面积。

3.1 单调栈（⭐）

时间复杂度 O(n) ，空间复杂度 O(n)
以 [2,1,5,6,2,3] 为例：
在这里插入图片描述

如图所示，当数组遍历到2时（第一张图中的三角处），触发条件，开始计算高度为 6 时的最大矩形面积，以及高度为 5 时的最大矩形面积（此时得到柱形图中矩形的最大面积 10）；然后当数组遍历到最后一个元素（我们人为补0的位置），触发条件（弹出栈中所有大于 0 的元素 ==> 相当于清空栈中元素，看看还有哪个高度的矩形面积没有被计算，然后计算一下），开始计算高度为 3/2/1 时的最大矩阵面积，所以这也是为什么要一开始人为改造数组，给数组首尾补 0 的原因，即 保证栈内元素非空，并且对数组中每种情况的高度都能计算一遍。

Note：还有需要注意的一点是（width = r - l - 1），这是因为我们对数组进行了补 0 操作，让其左边界定位到了当前元素的左第一小处，所以需要额外减 1，这个地方也可以在给左边界赋值的时候人为加1。

class Solution {
    // Solution1：单调栈

    // 为了数据的正确进行，要改装一下 输入数组，即 为其首尾加0
    // 1. 为什么要在heights最前面加0？
    // 因为没有在heights前加0，不能保证stack不为空，所以left的值就需要赋初始值0
    // 2. 为什么要在heights最后面加0？
    // 在最后加0可以保证矩形高度都是递增的特殊情况下ans也能进行计算
    // 简言之：我们要找每个柱子的左右边界，那么首个柱子缺乏左边界，末尾柱子缺乏右边界

    public int largestRectangleArea(int[] heights) {
        // 无效输入判断
        int len = heights.length;
        if (len <= 0) return -1;
        // 改造数组，为其前后补0
        int[] newHeights = new int[len+2];
        for (int i = 1; i < newHeights.length-1; i++) {
            newHeights[i] = heights[i-1];
        }
        // 构建单调递减栈，找到左右边第一小
        Stack<Integer> stack = new Stack<>();
        // 记录数组中可能的最大面积
        int maxArea = 0;
        // 遍历改造数组
        for (int i = 0; i < newHeights.length; i++) {
            // 栈非空，且当前数组元素小于栈顶元素时，弹出栈顶
            while (!stack.isEmpty() && newHeights[i] < newHeights[stack.peek()]) {
                // 记录当前高度的下标索引（当遇到当前数组元素小于栈顶元素时，即找到了当前高度区域面积的右边界）
                int idx = stack.pop();
                // 左边界
                int l = stack.peek();
                // 右边界
                int r = i;
                // 存储当前高度的最大面积
                maxArea = Math.max(maxArea, newHeights[idx] * (r - l - 1));
            }
            stack.push(i);
        }
        return maxArea;
    }
}

3.2 公式优化（s=(right-left-1)*height[i]）

更多内容可参考：柱状图中最大的矩形（难）
根据上面的分析，我们知道对于第i根柱子所围成的最大矩形是 s=(right-left-1)*height[i]，其中 right 是右边比它小的柱子的下标，left 是左边比它小的柱子的下标，height[i] 是当前柱子的高度。那么只要我们知道了每根柱子左右两边比它小的值，我们就可以求出最大面积。

我们可以通过以下代码找到当前柱子左边比它小的柱子的下标：

    for (int i = 1; i < height.length; i++) {
        int p = i - 1;
        while (p >= 0 && height[p] >= height[i]) {
            p = leftLess[p];
        }
        leftLess[i] = p;
    }

找右边第一小也同理，于是我们就得到了以下代码：

class Solution {
    public int largestRectangleArea(int[] height) {
        if (height == null || height.length == 0) {
            return 0;
        }
        //存放左边比它小的下标
        int[] leftLess = new int[height.length];
        //存放右边比它小的下标
        int[] rightLess = new int[height.length];
        rightLess[height.length - 1] = height.length;
        leftLess[0] = -1;

        //计算每个柱子左边比它小的柱子的下标
        for (int i = 1; i < height.length; i++) {
            int p = i - 1;
            while (p >= 0 && height[p] >= height[i]) {
                p = leftLess[p];
            }
            leftLess[i] = p;
        }
        //计算每个柱子右边比它小的柱子的下标
        for (int i = height.length - 2; i >= 0; i--) {
            int p = i + 1;
            while (p < height.length && height[p] >= height[i]) {
                p = rightLess[p];
            }
            rightLess[i] = p;
        }
        int maxArea = 0;
        //以每个柱子的高度为矩形的高，计算矩形的面积。
        for (int i = 0; i < height.length; i++) {
            maxArea = Math.max(maxArea, height[i] * (rightLess[i] - leftLess[i] - 1));
        }
        return maxArea;
    }
}

在这里插入图片描述

五、小结

专题突破第一周：单调栈 739 、503 、901、84，一共分为四小题：

题目一：739. 每日温度，Medium，找右第一大；
题目二：503. 下一个更大元素 II，Medium，同样也是找右第一大，但不同之处在于输入参数为循环数组，需要两次遍历并对下标进行求余计算；
题目三：901. 股票价格跨度，Medium，找左第一大，但由于该题没有给定输入参数（eg：数组等存储元素的数据结构），所以此处需要我们自己定义一个二元数对（int[] 或哈希表）来存储下标或结果；
题目四：84. 柱状图中最大的矩形，Hard，1. 找左右第一小，该题由于要计算矩形的面积，那么就需要我们去找到当前柱子的左右第一小柱子的下标来作为左右边界（宽度），我们可以从左向右遍历，去找左第一小，如果当前元素小于栈顶元素，则弹出栈顶元素，直至栈顶元素小于或等于当前元素，那么当前元素的下标即为右边界，当前栈顶元素的下标即为左边界，被弹出的栈顶元素对应数组的值即为高（单调栈做法）；2. 除了单调栈的做法外，我们也可以直接从当前元素位置循环去找当前元素的左右第一小，然后用公式计算得出最大矩形（效率更高）。