“I hear and I forget. I see and I remember. I do and I understand”——Confucius

人类计算二进制数的方法

我们先计算本位的结果，称为加法位；再计算是否进位，称为进位位。

搭建二进制加法器

我们用逻辑门来搭建二进制加法器。它的思想与人类计算的思想很相似，先计算加法位，再计算进位位。我们先看如何计算进位位。

搭建单个进位位和加法位

搭建进位位的逻辑电路

进位位的输出表如下所示：

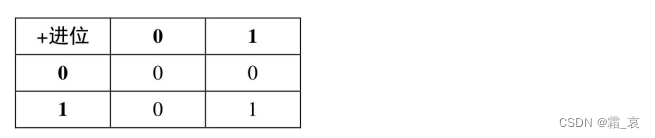
这和与门的输出是相同的，因此使用与门就可以表示进位位。

搭建加法位的逻辑电路

加法位的输出表如图所示：

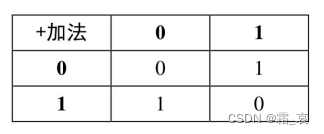
与进位位不同，这个输出表不太容易得到。我们先思考或门和与非门的输出表：

1. 或门：
   

2. 与非门：

这两个逻辑门的输出表和加法位比较相似。这里使用离散数学的知识，用真值表把我们想要的结果列出来：

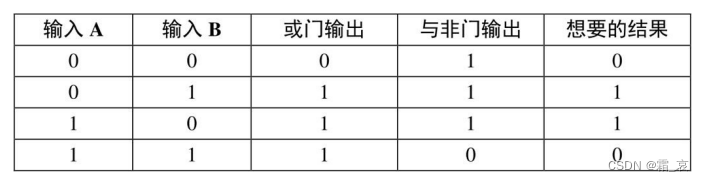
不难看出，我们想要的结果就是

（A OR B）AND（A NAND B）

也就是：

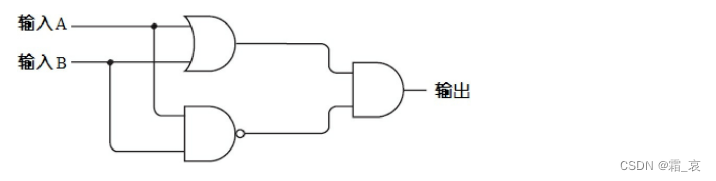
这个电路可以简化成一个符号，即异或门（XOR），当两个输入不一样时，输出为1。用符号表示就是：

半加器和全加器

我们将产生加法位和进位位的门连接在一起：

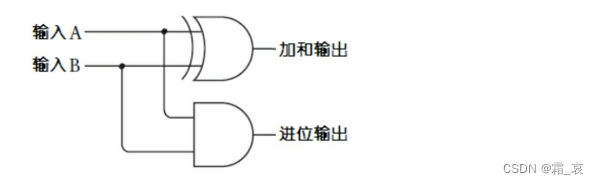
这就是半加器。用符号表示就是：

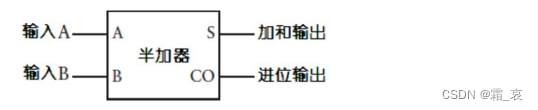
思考一下，我们在做竖式运算的时候，除了个位，其余位都要加上上一位的进位，因此需要一个三个输入的逻辑电路才行（这一位的两个输入和上一位的进位），我们可以用下述电路来表示：

每一个半加器可以把两个一位的二进制数相加，左上角的进位输入是上一位的进位位。这个电路的原理和竖式运算完全相同。
注意，右下角计算该位的进位输出时，我们也可以用半加器来计算，但经过实践，可以发现不会有两个CO都是1的情况，因此使用或门就可以产生与半加器相同的效果。
这个电路就是全加器，我们用符号表示就是：

连接全加器

我们的最终目标是要搭建一个8位二进制数的加法器。为此，我们需要连接8个全加器。

1. 最低位的全加器的进位输入为0，因此用下图表示：
   
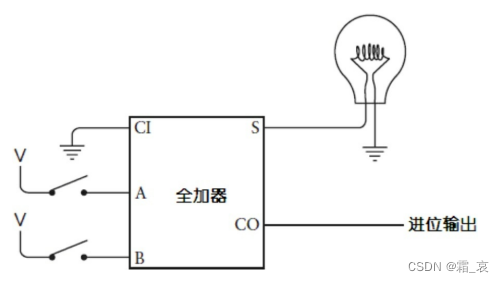
2. 中间的全加器是正常用法：
   
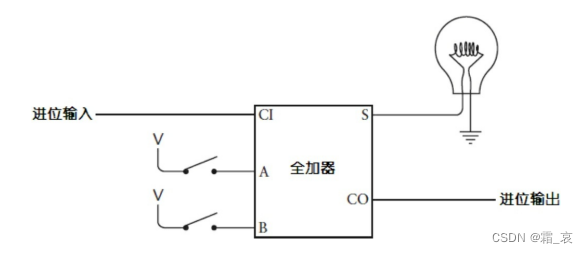
3. 最后的全加器需要把进位输出也展示出来：
   

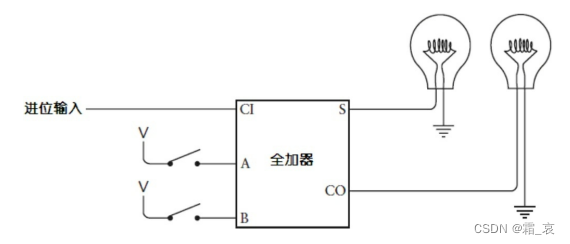
最后，我们构建了一个八位的加法器：

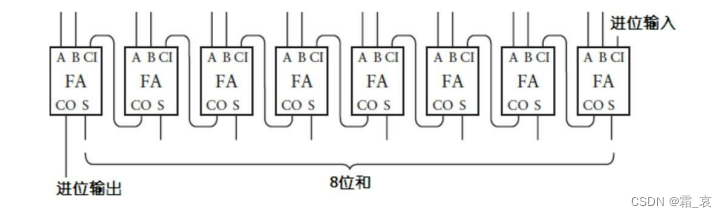
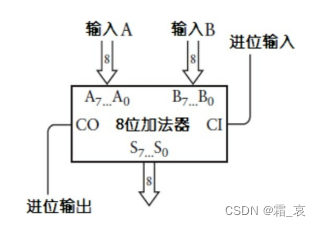
用符号表示就是：


我是霜_哀，在算法之路上努力前行的一位萌新，感谢你的阅读！如果觉得好的话，可以关注一下，我会在将来带来更多更全面的算法讲解！