Transformer 位置编码代码解析
Transformer 的 Multi-Head-Attention 无法判断各个编码的位置信息。因此 Attention is all you need 中加入三角函数位置编码(sinusoidal position embedding),表达形式为:
P
E
(
p
o
s
,
2
i
)
=
sin
(
pos
/
1000
0
2
i
/
d
modal
)
P
E
(
p
o
s
,
2
i
+
1
)
=
cos
(
pos
/
1000
0
2
i
/
d
model
)
\begin{aligned} & P E_{(\mathrm{pos}, 2 i)}=\sin \left(\operatorname{pos} / 10000^{2 i / d_{\text {modal }}}\right) \\ & P E_{(p o s, 2 i+1)}=\cos \left(\operatorname{pos} / 10000^{2 i / d_{\text {model }}}\right) \end{aligned}
PE(pos,2i)=sin(pos/100002i/dmodal )PE(pos,2i+1)=cos(pos/100002i/dmodel )
其中 pos 是单词位置,i = (0,1,... d_model) 所以d_model为 512 情况下,第一个单词的位置编码可以表示为:
P
E
(
1
)
=
[
sin
(
1
/
1000
0
0
/
512
)
,
cos
(
1
/
1000
0
0
/
512
)
,
sin
(
1
/
1000
0
2
/
512
)
,
cos
(
1
/
1000
0
2
/
512
)
,
…
]
\begin{aligned} & P E(1)=\left[\sin \left(1 / 10000^{0 / 512}\right), \cos \left(1 / 10000^{0 / 512}\right), \sin \left(1 / 10000^{2 / 512}\right), \cos \right. \\ & \left.\left(1 / 10000^{2 / 512}\right), \ldots\right] \end{aligned}
PE(1)=[sin(1/100000/512),cos(1/100000/512),sin(1/100002/512),cos(1/100002/512),…]
代码
import numpy as np
import matplotlib.pyplot as plt
def get_angles(pos, i, d_model):
angle_rates = 1 / np.power(10000, (2 * (i//2)) / np.float32(d_model))
return pos * angle_rates
def positional_encoding(position, d_model):
angle_rads = get_angles(np.arange(position)[:, np.newaxis],
np.arange(d_model)[np.newaxis, :],
d_model)
# apply sin to even indices in the array; 2i
angle_rads[:, 0::2] = np.sin(angle_rads[:, 0::2])
# apply cos to odd indices in the array; 2i+1
angle_rads[:, 1::2] = np.cos(angle_rads[:, 1::2])
pos_encoding = angle_rads[np.newaxis, ...]
return pos_encoding
tokens = 10
dimensions = 64
pos_encoding = positional_encoding(tokens, dimensions)
print (pos_encoding.shape)
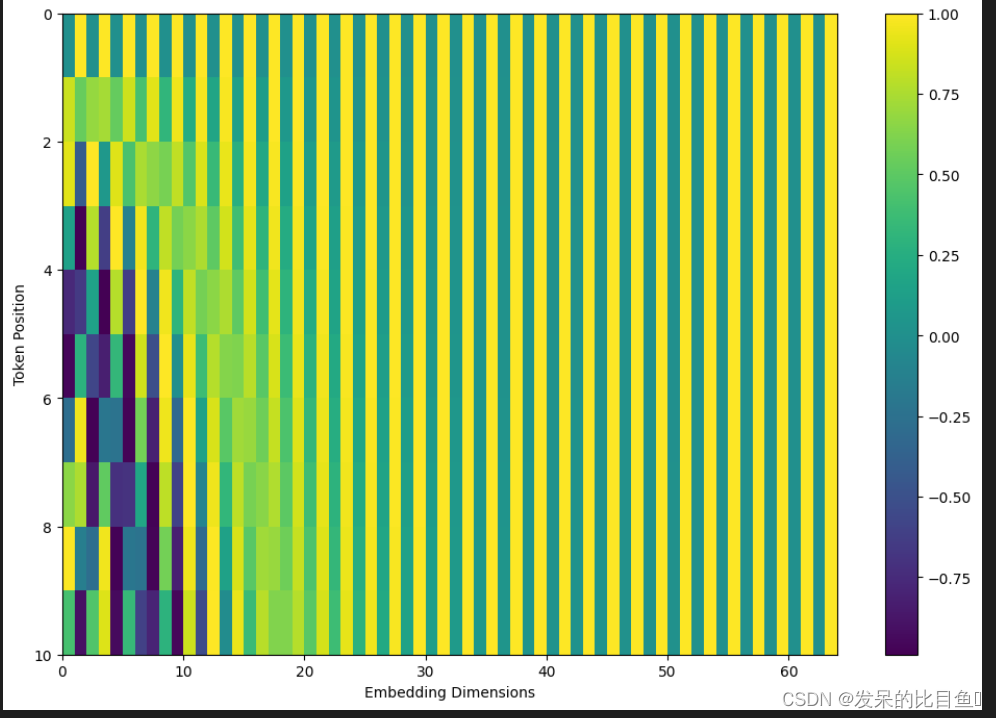
plt.figure(figsize=(12,8))
plt.pcolormesh(pos_encoding[0], cmap='viridis')
plt.xlabel('Embedding Dimensions')
plt.xlim((0, dimensions))
plt.ylim((tokens,0))
plt.ylabel('Token Position')
plt.colorbar()
plt.show()