title: 24考研数学每日一题Latex版(带解析)
date: 2023-01-28 11:49:26
plugins:
- mathjax
tags: - 学习
- 考研
categories: - 考研数学
题目来源于武老师的每日一题,答案是自己做的,不太严谨,仅供参考

2022年12月1日
知识点:求极限(1的无穷次方型)
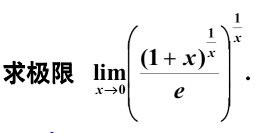
答案:
原式
=
lim
x
→
0
(
(
1
+
x
)
1
x
e
)
1
x
=
lim
x
→
0
e
1
x
l
n
(
(
1
+
x
)
1
x
e
−
1
+
1
)
=
lim
x
→
0
e
1
x
(
(
1
+
x
)
1
x
−
e
e
)
=
lim
x
→
0
e
(
(
1
+
x
)
1
x
−
e
e
x
)
=
lim
x
→
0
e
(
e
1
x
l
n
(
1
+
x
)
−
e
e
x
)
=
lim
x
→
0
e
(
(
l
n
(
1
+
x
)
x
−
1
)
e
ε
e
x
)
=
lim
x
→
0
e
(
(
l
n
(
1
+
x
)
−
x
x
)
e
ε
e
x
)
=
lim
x
→
0
e
1
e
(
(
l
n
(
1
+
x
)
−
x
x
)
e
ε
x
)
=
lim
x
→
0
e
1
e
(
l
n
(
1
+
x
)
−
x
x
2
)
=
e
−
1
2
\begin{aligned} 原式&=\lim_{x \to 0} (\frac{(1+x)^{\frac{1}{x} }}{e} )^{\frac{1}{x} } \\ &=\lim_{x \to 0}e^{\frac{1}{x}ln(\frac{(1+x)^{\frac{1}{x} }}{e}-1+1) } \\ &=\lim_{x \to 0}e^{\frac{1}{x}(\frac{(1+x)^{\frac{1}{x} }-e}{e} ) } \\ &=\lim_{x \to 0}e^{(\frac{(1+x)^{\frac{1}{x} }-e}{ex} ) } \\ &=\lim_{x \to 0}e^{(\frac{e^{\frac{1}{x}ln(1+x) }-e}{ex} ) } \\ &=\lim_{x \to 0}e^{(\frac{(\frac{ln(1+x)}{x}-1)e^\varepsilon }{ex} ) } \\ &=\lim_{x \to 0}e^{(\frac{(\frac{ln(1+x)-x}{x})e^\varepsilon }{ex} ) } \\ &=\lim_{x \to 0}e^{\frac{1}{e} (\frac{(\frac{ln(1+x)-x}{x})e^\varepsilon }{x} ) } \\ &=\lim_{x \to 0}e^{\frac{1}{e} (\frac{ln(1+x)-x }{x^2} ) } \\ &=e^{-\frac{1}{2} } \end{aligned}
原式=x→0lim(e(1+x)x1)x1=x→0limex1ln(e(1+x)x1−1+1)=x→0limex1(e(1+x)x1−e)=x→0lime(ex(1+x)x1−e)=x→0lime(exex1ln(1+x)−e)=x→0lime(ex(xln(1+x)−1)eε)=x→0lime(ex(xln(1+x)−x)eε)=x→0limee1(x(xln(1+x)−x)eε)=x→0limee1(x2ln(1+x)−x)=e−21






![[算法前沿]--014- AIGC和LLM下的Prompt Tuning微调范式](https://img-blog.csdnimg.cn/img_convert/8eb17d0ab8d09defd282366dd26ae56c.jpeg)