struc2vec: Learning Node Representations from Structural Identity

learning latent representations for the structural identity of nodes. ： 从结构特征中学习节点潜在表示
node representation : 节点表示
structural identity : 结构特征

struct2Vec是一个新的和灵活的学习框架，从结构标识中学习节点的特征。使用层次结构在不同尺度上度量节点相似性，并构建一个多层图来编码结构相似性并为节点生成结构上下文

• 它在学习捕获结构特征方面展现出优异的性能表现，所以算法在分类任务中改进，主要是依赖于结构特征的学习上

不同的节点在网络中大致中发挥着相似的功能，因此，通过节点在网络结构中发挥的功能，节点被划分成相同的类别

###节点的结构特征度量方法

1. 距离
   利用节点邻域的距离函数用于度量所有节点对之间的距离，然后通过聚类或匹配将节点放置到等价的类中
2. 递归
   构造一个对相邻节点的递归，然后迭代展开直到收敛，用最终的值来确定等价类

这两种方法各有优劣，所以我们提出了代替的方法

基于无监督的节点结构特征的学习，在分类和预测任务上表现优异。
在领域内，对节点的context进行广义的编码，w是随机游走的步长；具有相同领域的节点
节点在领域内具有相似的节点集应该具有相似的潜在表征

关键点：

1. 大多数真实网络中的许多节点特征都表现出很强的同质性

example：两个具有相同政治倾向的博客更有可能被联系起来，而不是随机地联系起来

2. 具有给定特征的节点的邻居更有可能具有相同的特征

在网络和潜在表示中接近的节点将倾向于共享特征，同理，网络中远的两个节点在潜在表示中倾向于分离，独立于它们的局部结构

• 结构等价性将不能被正确地捕获在潜在的表示中

然而，如果对更依赖结构同一性而更少依赖同质性的特征进行分类，那么这些最近的方法很可能会被捕获结构同一性的潜在表现所超越

算法核心思想

1. 评估节点之间独立于节点和边缘的结构相似性以及它们在网络中的位置。
   将考虑两个具有相似局部结构的节点，独立于网络位置和节点标签，且也不需要网络连接，并且在不同连接的组件中识别出结构相似的节点
2. 建立一个层次结构来度量结构上的相似性，对结构相似的概念越来越严格。
   在层次结构的底部，节点之间的结构相似性只取决于它们的程度，而在层次结构的顶部，相似性取决于整个网络。
3. 为节点生成随机context，来划分通过加权随机游走历多层图观察到的结构相似的节点。
   出现在相似的context中的两个节点很可能具有相似的结构，这种context可以通过语言模型来学习节点的潜在表示
4. 节点的潜在表示之间的距离应该与它们的结构相似性密切相关。具有相同结构特征中，而具有不同结构特征的节点应该相距很远
5. 节点的结构标识必须独立于它在网络中的“位置”
6. 节点的潜在表示不应该依赖于任何节点或边属性，包括节点标签
7. 相似性度量应该是分层的，并应对不断增加的邻域大小，捕获更多重复的结构相似性概念
8. 具有相同度的两个节点在结构上是相似的，但是如果它们的邻居也具有相同的度，那么它们在结构上甚至更相似

总结：Struct2Vec算法不要求任何特定的结构相似性度量或表征学习框架

Example：

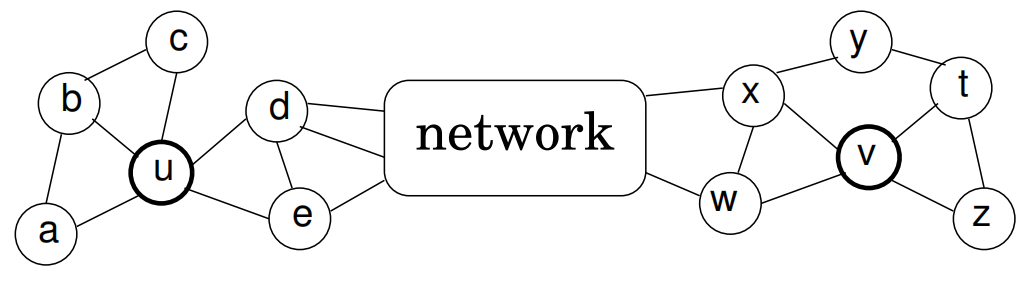
• U和V两个节点结构相似，图的度也相似，但是它们间的距离很远

DeepWalk和node2vec不能捕捉到结构特征，在分类任务中节点标签更依赖于结构特征，struct2vec在分类任务中更优越

DeepWalk算法

核心词：node embedding

基础知识补充：

什么是context？

如果两个不同的单词有着非常相似的“上下文”（也就是窗口单词很相似，比如“Kitty climbed the tree”和“Cat climbed the tree”），那么通过我们的模型训练，这两个单词的嵌入向量将非常相似。
那么两个单词拥有相似的“上下文”到底是什么含义呢？比如对于同义词“intelligent”和“smart”，我们觉得这两个单词应该拥有相同的“上下文”。而例如”engine“和”transmission“这样相关的词语，可能也拥有着相似的上下文。

实际上，这种方法实际上也可以帮助你进行词干化（stemming），例如，神经网络对”ant“和”ants”两个单词会习得相似的词向量。

词干化（stemming）就是去除词缀得到词根的过程。

什么是embedding

这个概念在深度学习领域最原初的切入点是所谓的Manifold Hypothesis（流形假设）。流形假设是指“自然的原始数据是低维的流形嵌入于(embedded in)原始数据所在的高维空间”。那么，深度学习的任务就是把高维原始数据（图像，句子）映射到低维流形，使得高维的原始数据被映射到低维流形之后变得可分，而这个映射就叫嵌入（Embedding）。Embedding其实就是一个映射，将单词从原先所属的空间映射到新的多维空间中，也就是把原先词所在空间嵌入到一个新的空间中去。比如Word Embedding，就是把单词组成的句子映射到一个表征向量。但后来不知咋回事，开始把低维流形的表征向量叫做Embedding，其实是一种误用。。。如果按照现在深度学习界通用的理解（其实是偏离了原意的）.
我们从直观角度上来理解一下，cat这个单词和kitten属于语义上很相近的词，而dog和kitten则不是那么相近，iphone这个单词和kitten的语义就差的更远了。通过对词汇表中单词进行这种数值表示方式的学习（也就是将单词转换为词向量），能够让我们基于这样的数值进行向量化的操作从而得到一些有趣的结论。比如说，如果我们对词向量kitten、cat以及dog执行这样的操作：kitten - cat + dog，那么最终得到的嵌入向量（embedded vector）将与puppy这个词向量十分相近。

• 综上：Embedding就是从原始数据提取出来的Feature，也就是那个通过神经网络映射之后的低维向量。

什么是Word2Vec？

Word2Vec是从大量文本语料中以无监督的方式学习语义知识的一种模型，它被大量地用在自然语言处理（NLP）中。那么它是如何帮助我们做自然语言处理呢？Word2Vec其实就是通过学习文本来用词向量的方式表征词的语义信息，即通过一个嵌入空间使得语义上相似的单词在该空间内距离很近。

Skip-Gram模型

参考链接：

Word2Vec模型中，主要有Skip-Gram和CBOW两种模型，从直观上理解，Skip-Gram是给定input word来预测上下文。而CBOW是给定上下文，来预测input word。

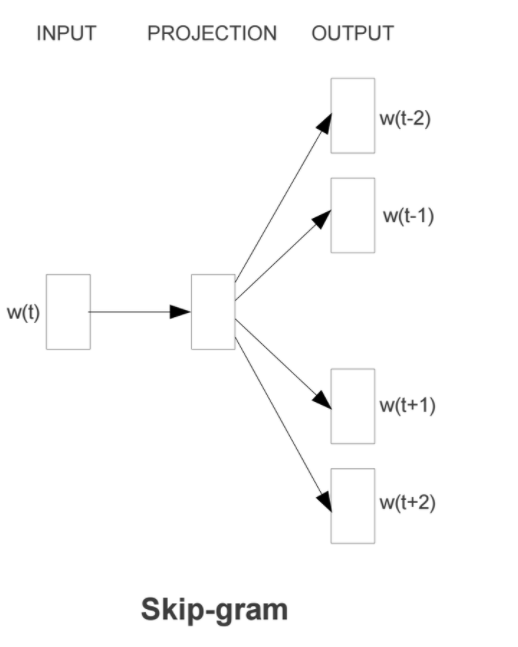
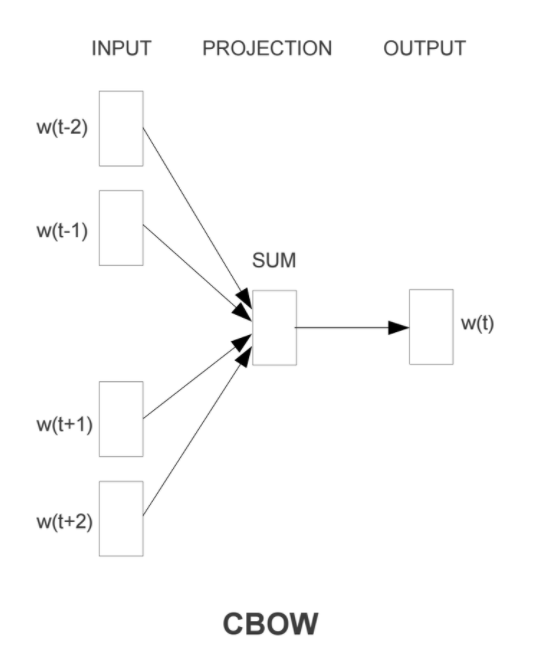
Skip-Gram模型实际上分为了两个部分，第一部分为建立模型，第二部分是通过模型获取嵌入词向量。Skip-Gram的整个建模过程实际上与自编码器（auto-encoder）的思想很相似，即先基于训练数据构建一个神经网络，当这个模型训练好以后，我们并不会用这个训练好的模型处理新的任务，我们真正需要的是这个模型通过训练数据所学得的参数，例如隐层的权重矩阵——后面我们将会看到这些权重在Skip-Gram中实际上就是我们试图去学习的“word vectors”。基于训练数据建模的过程，我们给它一个名字叫“Fake Task”，意味着建模并不是我们最终的目的。

上面提到的这种方法实际上会在无监督特征学习（unsupervised feature learning）中见到，最常见的就是自编码器（auto-encoder）：通过在隐层将输入进行编码压缩，继而在输出层将数据解码恢复初始状态，训练完成后，我们会将输出层“砍掉”，仅保留隐层。

The Fake Task

我们在上面提到，训练模型的真正目的是获得模型基于训练数据学得的隐层权重。为了得到这些权重，我们首先要构建一个完整的神经网络作为我们的“Fake Task”，后面再返回来看通过“Fake Task”我们如何间接地得到这些词向量。

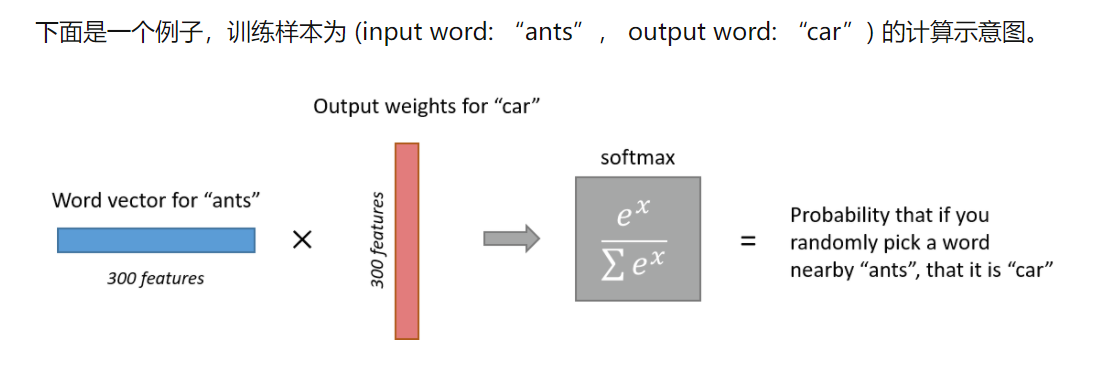
• Example:接下来我们来看看如何训练我们的神经网络。假如我们有一个句子“The dog barked at the mailman”。

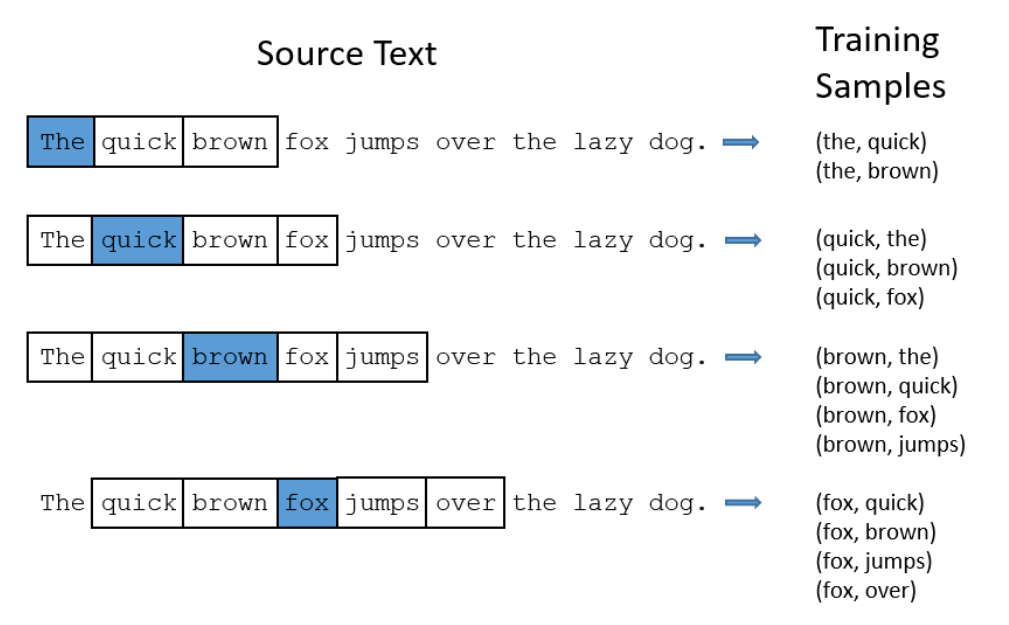
• 我们将通过给神经网络输入文本中成对的单词来训练它完成上面所说的概率计算。下面的图中给出了一些我们的训练样本的例子。我们选定句子“The quick brown fox jumps over lazy dog”，设定我们的窗口大小为2,window_size=2,也就是说我们仅选输入词前后各两个词和输入词进行组合。下图中，蓝色代表input word，方框内代表位于窗口内的单词

• 模型表示：首先，我们都知道神经网络只能接受数值输入，我们不可能把一个单词字符串作为输入，因此我们得想个办法来表示这些单词。最常用的办法就是基于训练文档来构建我们自己的词汇表（vocabulary）再对单词进行one-hot编码。

神经网络结构：

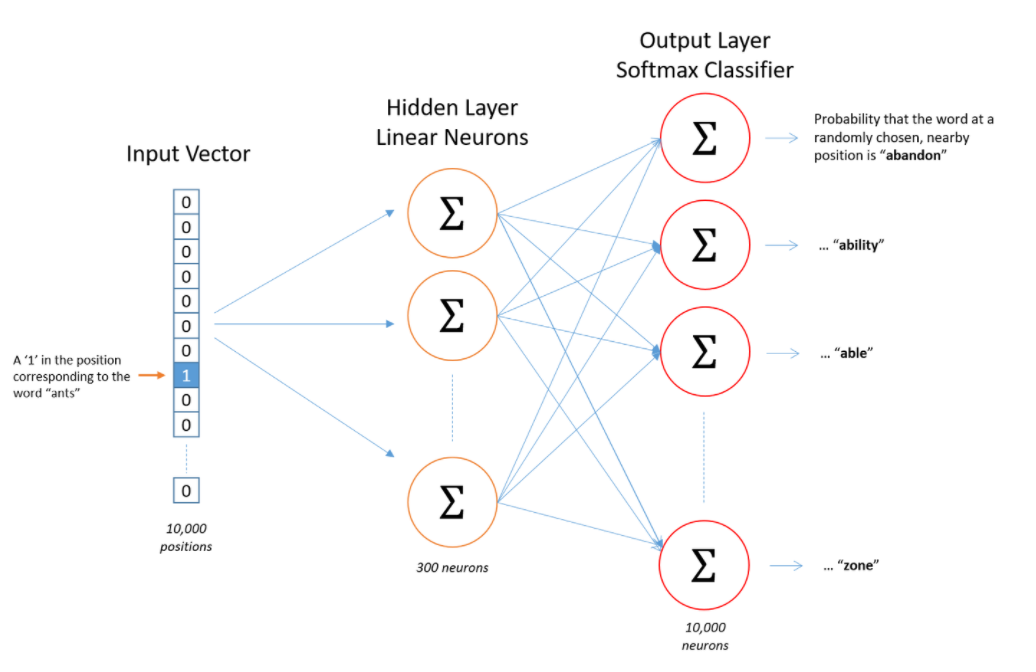
• 隐层没有使用任何激活函数，但是输出层使用了sotfmax。

我们基于成对的单词来对神经网络进行训练，训练样本是 ( input word, output word ) 这样的单词对，input word和output word都是one-hot编码的向量。最终模型的输出是一个概率分布

• 隐层

说完单词的编码和训练样本的选取，我们来看下我们的隐层。如果我们现在想用300个特征来表示一个单词（即每个词可以被表示为300维的向量）。那么隐层的权重矩阵应该为10000行，300列（隐层有300个结点）

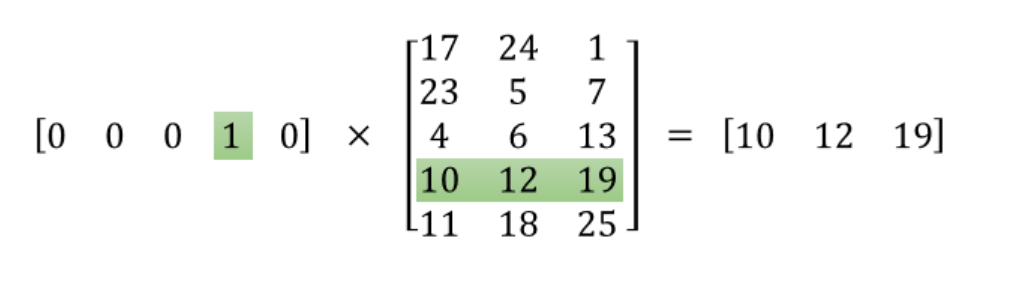
在自然语言处理领域，给稀疏数据生成密集嵌入向量

• 矩阵是非常稀疏的！我们来看一下上图中的矩阵运算，左边分别是1 x 5和5 x 3的矩阵，结果应该是1 x 3的矩阵，按照矩阵乘法的规则，结果的第一行第一列元素为，同理可得其余两个元素为12，19。如果10000个维度的矩阵采用这样的计算方式是十分低效的。

• 为了有效地进行计算，这种稀疏状态下不会进行矩阵乘法计算，可以看到矩阵的计算的结果实际上是矩阵对应的向量中值为1的索引，上面的例子中，左边向量中取值为1的对应维度为3（下标从0开始），那么计算结果就是矩阵的第3行（下标从0开始）—— [10, 12, 19]，这样模型中的隐层权重矩阵便成了一个”查找表“（lookup table），进行矩阵计算时，直接去查输入向量中取值为1的维度下对应的那些权重值。隐层的输出就是每个输入单词的“嵌入词向量”。

• 输出：经过神经网络隐层的计算，ants这个词会从一个1 x 10000的向量变成1 x 300的向量，再被输入到输出层。输出层是一个softmax回归分类器，它的每个结点将会输出一个0-1之间的值（概率），这些所有输出层神经元结点的概率之和为1。

node2vec算法

优化目标

是将顶点映射为embedding向量的映射函数,对于图中每个顶点，通过采样策略 采样出的顶点的近邻顶点集合。

node2vec优化的目标是给定每个顶点条件下，令其近邻顶点（如何定义近邻顶点很重要）出现的概率最大

两个假设：1.条件独立性假设 2.特征空间对称性假设

顶点序列采样策略

node2vec依然采用随机游走的方式获取顶点的近邻序列，不同的是node2vec采用的是一种有偏的随机游走。

• 参数p控制重复访问刚刚访问过的顶点的概率
• q 控制着游走是向外还是向内，若 q>1 ，随机游走倾向于访问和 接近的顶点(偏向BFS)。若 q<1，倾向于访问远离 的顶点(偏向DFS

算法步骤

Step 1：评估结构相似度

我们需要定义出一种独立于nodes和edges的相似性定义， 此外，这种相似性度量应该是分层的，并应对不断增加的邻域大小， 捕捉更多结构相似性。 直观地说，具有相同的度的两个节点在结构上是相似的，但如果它们的邻居也具有相同的程度，那么它们的结构更加更相似，以无权图为例，如果某两个节点的度为5，则其结构完全相似

代码学习链接：https://blog.csdn.net/u012151283/article/details/87255951

Step 3：为节点生成上下文

多层图结构（捕获两两间的结构相似度完全不带节点信息）会为每个节点生成上下文

1. sturct2vec是通过随机漫步（马尔可夫链状态连）生成节点序列，但是在这是通过偏重的随机漫步，根据图矩阵的权重
2. 随机漫步每一步之前，都要看是否要改变层级（概率大于0就不用）

随机漫步比较喜欢相似度比较高的节点，避免相似度低的节点

• 如果呆在当前层级（p>0）：
  节点u到v的概率定义为：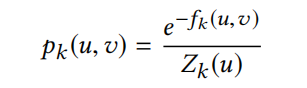

  

Z是在k层词向量u的归一化因子
定义：

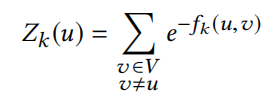
-如果概率为1-q，需要改变层级，移动到相关节点然后层级+1或者-1，然后定义边权重

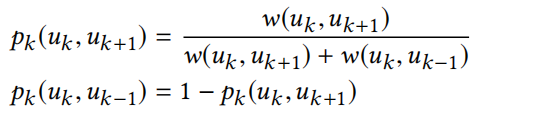
注意，每次在一个层中随机漫步时，它都将当前顶点作为其上下文的一部分，独立于层级
所以，词向量u不仅在k层有上下文，而且在k+1层也有上下文，因为结构相似度不能随着层级上升而增加

核心：这是一个跨层的层次化上下文的概念

整个过程：先在第一层在相关联的节点间开始随机漫步；随机漫步会随机游走有一个固定的和
相对较短的长度（步数）,然后过程中会重复一定次数导致多次的独立漫步

学习语言模型

关键词：词向量映射，节点序列
SKip-Gram算法会生成节点序列代替词序列，最大化上下文在序列中的可能性 ；而struct2vec采用多层图的随机漫步，而且采用层级化的Softmax映射（通过一个二分类的树模型来描述，节点和层级对应）

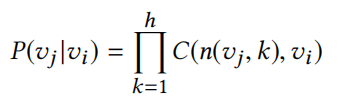
节点嵌入这里，不仅可以用SKip-Gram其他的技术也可以用

复杂度和最优化

考虑一下计算的复杂度，在每一层中我们都要计算每个节点对之间的结构距离，并且采用的是DTW距离来计算两个序列之间的距离，复杂度O（n2），每层有2n个节点对，网络中最大的度为k，总时间复杂度为O（k*n3）

优化思路一： 减小度序列的长度

因为计算序列中的每一个度，代价太大，而且很多节点在网络中都有相同的度，所以我们要提出了压缩有度序列（具有度和事件发生次数的元组），来减小计算量

更换DTW距离：

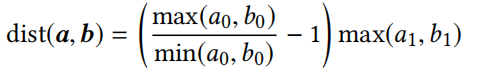
• 注意一点，用压缩有序度序列去计算原始序列的化可能会产生相同的度，DTW距离也相似；但是序列本身已经缩小了，DTW距离也会跟着变化，所以不产生影响

优化思路二：减少成对的相似度计算

原始框架评估每个层 k 的每个节点对之间的相似性，显然这似乎是不必要的， 考虑两个节点如果具有非常不同的度，则它们的结构距离即使在底层（k=0）层都会差异很大， 因此，它们之间的edge的权重就会很小， 这就导致了在为这些节点生成上下文时，**随机游走不太可能遍历这个edge。 因此，在M中没有这个edge影响很微小； 我们将成对相似性计算的数量限制在每个节点： **

让Ju表示在层次图结构中M中节点u的邻居的节点集，这对于每个layer都是相同的， ju应该有结构上和node u 结构最相似的节点， 为了确定Ju，我们取与u最相似的度的节点，可以通过对网络中所有节点的有序度序列(对于节点u的degree)执行二分法，并在每个方向上取Log（n）个连续节点来计算 ，实际上就是减少了计算的点，本来要计算n个相近的nodes，现在就计算logn个相近的nodes；保存的edge的空间复杂度也从O（n2）变成O(logn)；

减少层数k

网络的直径k∗决定了层次结构图M中的层数。 然而，对于许多网络来说，直径可能比平均距离大得多（极端的例子，graph中两个nodes的距离为1000 hop，而其它nodes和其中一个nodes的距离只有1 hop）。 此外，评估两个节点之间的结构相似性的重要性随着k的增大而降低，因为当k接近k的时候，即越来越趋于层级结构M的顶层的时候， **度序列的长度变得相对较短（层数越高，一个nodes的k hop处的节点越少），则fk(u,v)和fk-1(y,v)之间的差异性越小，因此实际上没必要建那么多层graph，我们取一个k<k来建立就好了**，比如设定为超参数，人工进行设置。