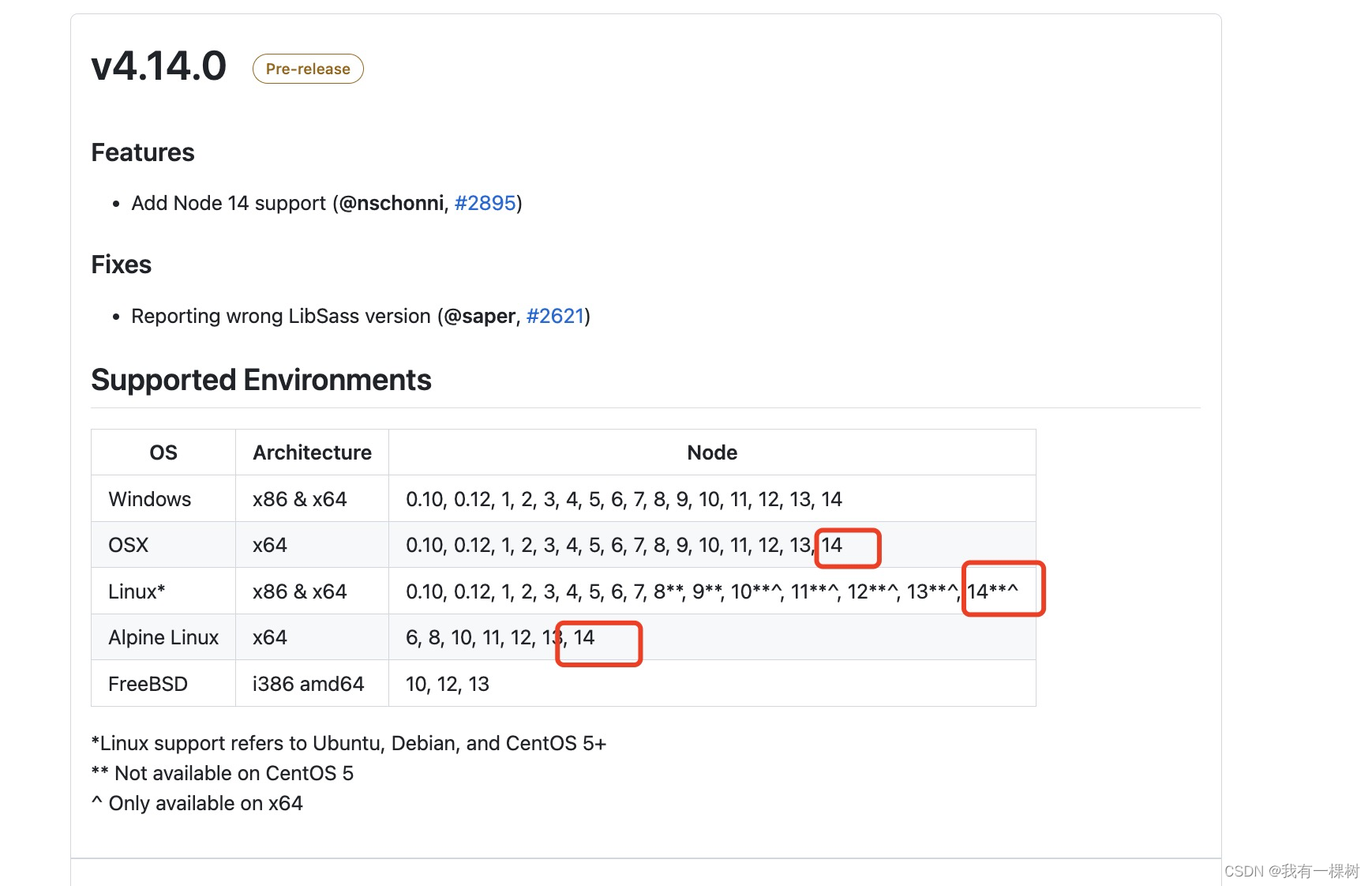
问:k最近邻分类模型是非线性模型。
答:正确。k最近邻分类模型是非线性模型,因为它的决策边界是由最近邻居点的类别决定的,而最近邻居点的分布通常是不规则的,因此决策边界也就不是线性的。因此,k最近邻分类模型是一种非参数化的方法,它能够适应各种复杂的数据集,并且不需要预先假设数据的分布形式。
最近有一批数据,通过4个特征来预测1个值,原来用线性回归和神经网络尝试过,准确率只能到40%左右。用KNN结合网格搜索和交叉验证,正确率达到了79%,没错,KNN解决回归问题也很赞。
问:已知五维空间中的两个点分别为(2,4,5,3,7)和(1,3,5,4,2),试计算这两个点的曼哈顿距离、欧几里得距离和切比雪夫距离。
答:
一、什么是KNN
KNN 算法,或者称 k-最近邻算法,是 有监督学习 中的 分类算法 。它可以用于分类或回归问题,但它通常用作分类算法。KNN就是K近邻算法(k-NearestNeighbor),所谓K最近邻,就是k个最近的邻居的意思,说的是每个样本都可以用它最接近的k个邻居来代表。
二、KNN 核心思想
KNN 的原理就是:当预测一个新样本的类别时,根据它距离最近的 K 个样本点是什么类别来判断该新样本属于哪个类别(多数投票)。
分析:K 值的影响
如果k值比较小,相当于我们用较小的领域内的训练样本对实例进行预测。这时,算法的近似误差(Approximate Error)会比较小,因为只有与输入实例相近的训练样本才会对预测结果起作用。但是,它也有明显的缺点:算法的估计误差比较大,预测结果会对近邻点十分敏感,也就是说,如果近邻点是噪声点的话,预测就会出错。因此,k值过小容易导致KNN算法的过拟合。
同理,如果k值选择较大的话,距离较远的训练样本也能够对实例预测结果产生影响。这时候,模型相对比较鲁棒,不会因为个别噪声点对最终预测结果产生影响。但是缺点也十分明显:算法的近邻误差会偏大,距离较远的点(与预测实例不相似)也会同样对预测结果产生影响,使得预测结果产生较大偏差,此时模型容易发生 欠拟合。
因此,在实际工程实践中,我们一般采用交叉验证的方式选取 k 值。通过以上分析可知,一般 k 值选得比较小,我们会在较小范围内选取 k 值,同时把测试集上准确率最高的那个确定为最终的算法超参数 k 。
三、KNN 的关键
实际上,KNN 算法有两个关键点:1. 点之间距离的计算;2. K 值的选取。
1. 距离计算
样本空间内的两个点之间的距离量度表示两个样本点之间的相似程度:距离越短,表示相似程度越高;反之,相似程度越低。
常用的距离量度方式包括:
- 闵可夫斯基距离
- 曼哈顿距离
- 欧氏距离
- 切比雪夫距离
- 余弦距离
1. 闵可夫斯基距离
闵可夫斯基距离本身不是一种距离,而是一类距离的定义。
其中,p是一个可变参数:
- 当p=1时,被称为曼哈顿距离;
- 当p=2时,被称为欧氏距离;
- 当p=∞时,被称为切比雪夫距离。
2. 曼哈顿距离

它测量两点之间的绝对值
3. 欧氏距离

欧氏距离(L2范数)是最易于理解的一种距离计算方法,源自欧氏空间中两点间的距离公式,也是最常用的距离量度。它测量两点之间的直线距离。
通常 KNN 算法中使用的是欧式距离。
4. 切比雪夫距离
切比雪夫距离是将2个点之间的距离定义为其各坐标数值差的最大值。对应L∞范数:

5. 余弦距离
余弦相似度的取值范围是[-1,1],相同两个向量的之间的相似度为1。
余弦相似度的定义公式为 :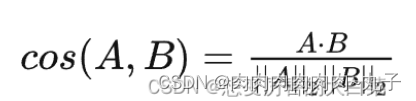
余弦距离的取值范围是[0,2]: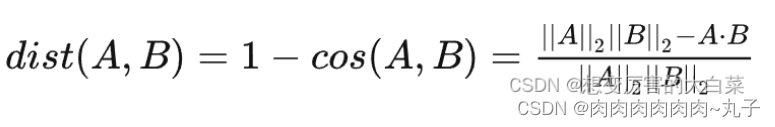
总结
这样我们就明白了如何计算距离。KNN 算法最简单粗暴的就是将预测点与所有点距离进行计算,然后保存并排序,选出前面 K 个值看看哪些类别比较多。但其实也可以通过一些数据结构来辅助,比如最大堆、KDTree,能够减小计算量,从而快速找到 K 个最近邻。