一、轻量化网络结构

目的就是减少网络的计算量

同时也需要保证模型的精确度

1. 分组卷积

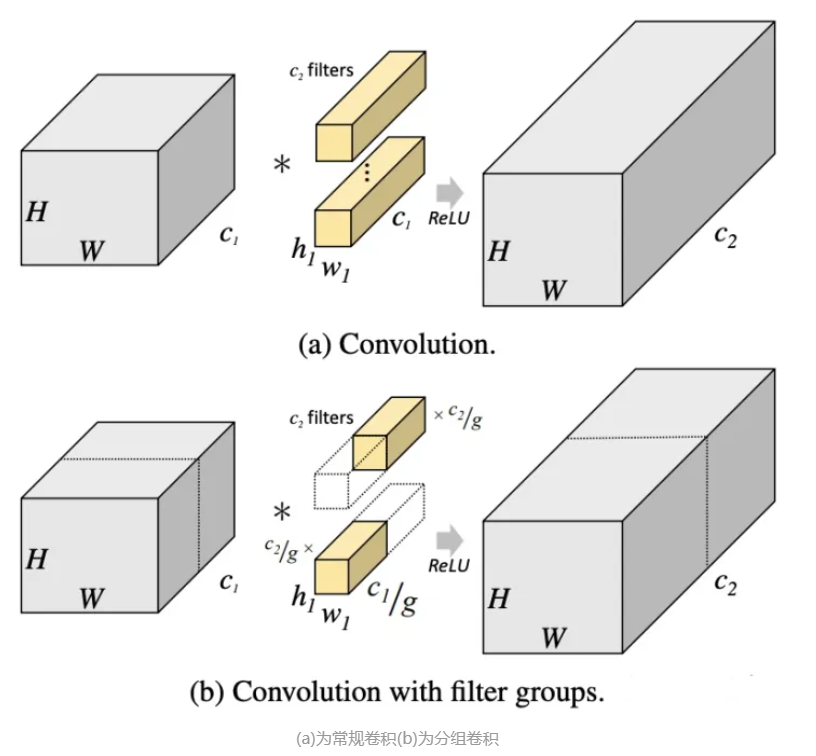
将输入特征图按通道均分为 g 组，然后对每一组进行常规卷积

由于分组后，每组输入特征图的通道数为 $\frac{C_{in}}{g}$ ，所以每个卷积核的通道数也降低到 $\frac{C_{in}}{g}$

由于每组内进行的是常规卷积，所以每组至少需要一个卷积核，即分组卷积输出通道数至少为 g，如果每组有 n 个卷积核，则输出 $C_{out} = n \times g, n \ge 1$ , 所以输出通道数是分组数的整数倍

综上所述，分组卷积中要求输入和输出通道数均能整除分组数 g

分组卷积的运算量和参数量的减少，归根结底是一个卷积核本身通道数减少为原来的 g 分之一

2. 深度可分离卷积

一种极致的分组卷积：当分组数等于输入通道数，且等于输出通道数，即 $g=C_{in}=C_{out}$ 时，我们把分组卷积称为深度可分离卷积,此时每个输出特征图仅仅与一个输入特征图相关，输入和输出一一对应。

由于深度可分离卷积每个输出通道仅由输入的一个通道得来，缺乏了输入通道之间的信息交换，所以通常在后面加一个1x1卷积来实现通道间的信息交换。

二、GhostNet

1. 动机

卷积的目的就是生成多个特征图，要减少卷积操作的运算量，在之前的网络结构中使用了分组卷积和深度可分离卷积的方法，这些是使用新的运算操作来替换掉传统的卷积操作。

GhostNet 这篇文件核心就是观察到通过传统卷积方式得到的特征图之间存在相似。那么能不能通过一种特殊的方式直接利用一个特征图生成另一个与之相似的特征图。

2. Ghost Module

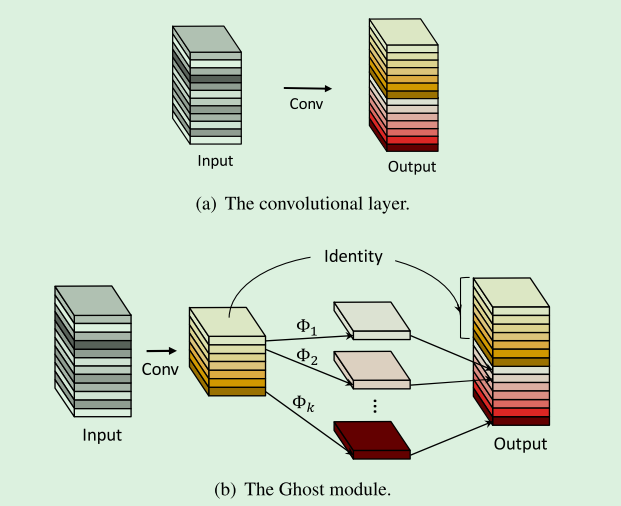
结合上图，传统卷积是 Input 经过 (a) 中卷积层得到通道数为 n 的 Output。

在 Ghost Module 中，Input 先经过传统卷积得到通道数为 m 的特征图，但是最终需要的 Output 是 n 的通道数，Ghost Module 就需要把 m 个通道扩展到 n 个通道。

论文中提到对每个固有特征图进行一系列的线性变换生成 s 个特征图。那么就有等式

$\times s$

如何实现扩充操作如下列式子所示：

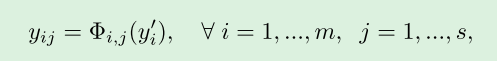
$y^{'}_{i}$ 表示由传统卷积得到的第 $i$ 个通道的特征图

$y_{ij}$ 表示由第 $i$ 个通道得到的第 $j$ 个特征图

$\Phi_{i,j}$ 表示线性变换，是指将第 $i$ 个通道的特征图，经过线性变换得到第 $j$ 个特征图

？？？疑问？？？

怎么选择 $y^{'}_{i}$ , 也就是怎么得到模块中所需要的通过传统卷积产生的特征图？
线性变换的具体操作是什么？

在代码中可以看见下面部分

        init_channels = math.ceil(oup / ratio)
        new_channels = init_channels*(ratio-1)

        self.primary_conv = nn.Sequential(
            nn.Conv2d(inp, init_channels, kernel_size, stride, kernel_size//2, bias=False),
            nn.BatchNorm2d(init_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

        self.cheap_operation = nn.Sequential(
            nn.Conv2d(init_channels, new_channels, dw_size, 1, dw_size//2, groups=init_channels, bias=False),
            nn.BatchNorm2d(new_channels),
            nn.ReLU(inplace=True) if relu else nn.Sequential(),
        )

    def forward(self, x):
        x1 = self.primary_conv(x)
        x2 = self.cheap_operation(x1)
        out = torch.cat([x1,x2], dim=1)