一.学习背景
在MySQL的学习中,我们了解到了索引的知识,而关于MySQL索引背后的数据结构,我们在这里进行学习.
首先,我们要了解到的是,MySQL的索引用到的数据结构为B+树.
使用B+树是因为,在数据量大的时候,内存不够用,大部分数据只能存放在磁盘上,只有需要的数据才加载到内存中。一般而言内存访问的时间约为 50 ns,而磁盘在 10 ms 左右。速度相差了近 5 个数量级,磁盘读取时间远远超过了数据在内存中比较的时间。这说明程序大部分时间会阻塞在磁盘 IO 上。这也正是我们采取B树的原因,普通的二叉树,红黑树等是没法满足这类需求的.所以我们采用新的存储方式.
二叉树是二分树,多分树是二叉树的推广。多分树主要适用于静态的索引数据文件,在插入和删除的时候需要把插入位置之后的每个记录都要向后移动,从而导致增加新的索引项和索引页块,需要对外存上的页块进行大量的调整。因此对于经常需要插入和删除的动态索引顺序文件,使用多分树并不合适,需要采用动态索引结构,即B树和B+树。
二.B树(B-树):
1.B树简介
B-树,这里的 B 表示 balance( 平衡的意思),B-树是一种多路自平衡的搜索树(B树是一颗多路平衡查找树)
它类似普通的平衡二叉树,不同的一点是B-树允许每个节点有更多的子节点。B树是可以认为是一个N叉搜索树.
B树的出现是为了弥补不同的存储级别之间的访问速度上的巨大差异,实现高效的 I/O。平衡二叉树的查找效率是非常高的,并可以通过降低树的深度来提高查找的效率。但是当数据量非常大,树的存储的元素数量是有限的,这样会导致二叉查找树结构由于树的深度过大而造成磁盘I/O读写过于频繁,进而导致查询效率低下。另外数据量过大会导致内存空间不够容纳平衡二叉树所有结点的情况。B树是解决这个问题的很好的结构。
2.B树概念:
一棵m阶B树是一棵平衡的m路搜索树,它或者是空树,或者是满足下列性质的树:
- 树中每个结点至多有m棵子树。(即至多含有m-1个关键字,两颗子树指针夹着一个关键字);
- 若根结点不是终端结点,则至少有两颗子树。(至少一个关键字);
- 除根结点外的所有非叶子结点至少有[m/2]棵子树。(即至少含有[m/2]-1个关键字);
- 所有的叶子结点出现在同一个层次上,不带信息。(就像是折半查找判断树中查找失败的结点)。
3.B树图示
由图可知,当节点的子树多了,叶子节点的个数就多了,说明可以保存的key值也变多了
这也就意味着,在保存key值相同个数的条件下,B树的高度相对于二叉搜索树就要低很多.这样的优势非常明显:磁盘 IO 的次数将大大减少!
4.B-树特点:
- 所有键值分布在整颗树中(索引值和具体data都在每个节点里)
- 任何一个关键字出现且只出现在一个结点中
- B树的每个节点可以存储N个key,N个key同时也划分出了N+1个区间
5.B树的查找代码:
Data* BTreeSearch(Root *node, Key key)
{
Data* data;
if(root == NULL)
return NULL;
data = BinarySearch(node);
if(data->key == key)
{
return data;
}else{
node = ReadDisk(data->next);
BTreeSearch(node, key);
}
}
二.B+树
1.B+树简介
B+树是应文件系统所需而产生的B树的变形树,那么可能一定会想到,既然有了B树,又出一个B+树,那B+树必然是有很多优点的。
B+树在B树上又做出了改进.B+树是B-树的变体,也是一种多路搜索树, 它与 B- 树的不同之处在于:
- 所有关键字存储在叶子节点出现,内部节点(非叶子节点并不存储真正的 data)
- 为所有叶子结点增加了一个链指针
2.B+树概念
B+树是B树上的一个修改或者改版:
- n棵子tree的节点包含n个关键字,不用来保存数据而是保存数据的索引。
- 所有的叶子结点中包含了全部关键字的信息,及指向含这些关键字记录的指针,且叶子结点本身依关键字的大小自小而大顺序链接。
- 所有的非终端结点可以看成是索引部分,结点中仅含其子树中的大(或小)关键字。
- B+树中,数据对象的插入和删除仅在叶节点上进行。
- B+树有2个头指针,一个是树的根节点,一个是小关键码的叶节点。
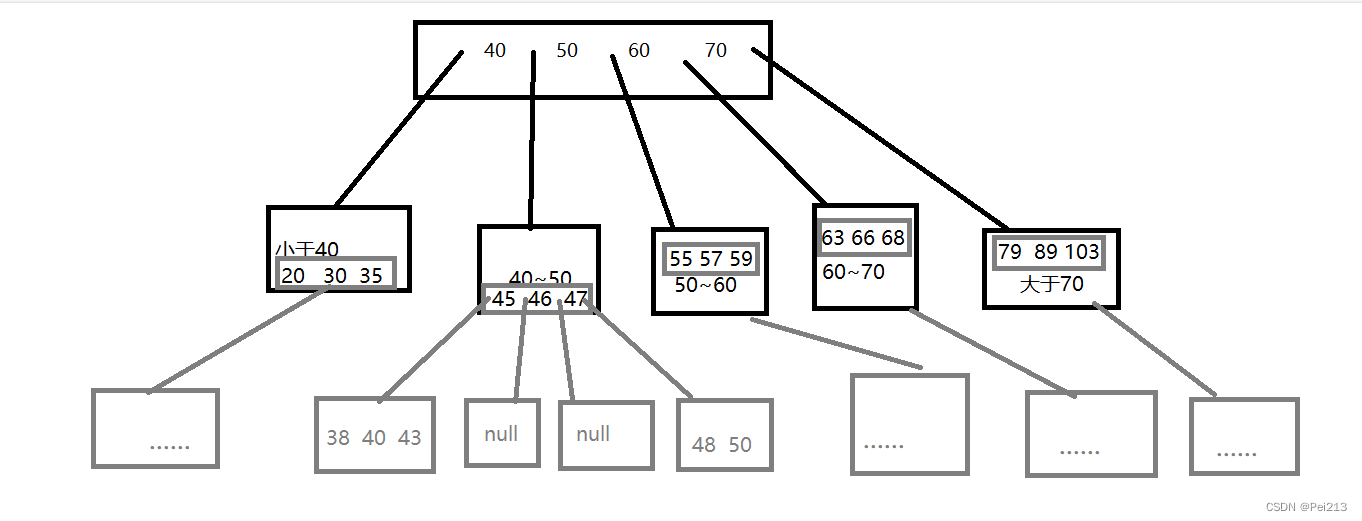
3.B+树图示

4.B+树特点:
1.B+树的每个节点可以存储N个key,N个key同时也划分出了N个区间(B树是N+1个区间)
2.B+树中每个节点中key的值,都会在子节点中也出现,并且是该子节点的最大值
3.B+树的叶子结点,是首尾相连的,类似于一个链表
4.B+树的叶子结点是完整的数据集合,只会在叶子结点这里存储每一行的数据,而不是叶子结点本身,只需要存储key值即可
三.B树和B+树的比较
B+树的优势:
1.一个节点保存更多的key,最终树的相对高度是更低的,查询的时候减少了IO次数(这点和B树相同)
2.所有的查询最后都会落到叶子节点上(查询任何一个数据,经过的IO访问次数是一样的)确保了稳定性,能够对程序的执行效率有更准确的评估.
3.B+树的所有的叶子结点可以构成链表,方便进行范围查询.
4.由于所有的数据都在叶子节点上,非叶子结点指存储key,这样非叶子节点占用的空间很小,(可能在内存中缓存或缓存一部分),又进一步减少了IO的次数
补充:B树的范围查找用的是中序遍历,而B+树用的是在链表上遍历。
| B树 | B+树 |
|---|---|
| 有m颗子树的节点中含有 m-1 个关键码 | 有m颗子树的节点中含有 m 个关键码 |
| B树中非叶子节点的关键码与叶子结点的关键码均不重复,它们共同构成全部的索引信息 | 所有的叶子结点中包含了完整的索引信息,包括指向含有这些关键字记录的指针,中间节点每个元素不保存数据,只用来索引 |
| B 树的非叶子节点包含需要查找的有效信息 | 所有的非叶子节点可以看成是高层索引, 结点中仅含有其子树根结点中最大(或最小)关键字 |