此栏目记录我学习《流畅的Python》一书的学习笔记,这是一个自用笔记,所以写的比较随意,随缘更新
用bisect来管理已排序的序列
bisect 模块包含两个主要函数,bisect 和 insort,两个函数都利用二分查找算法来在有序序列中查找或插入元素。
用bisect来搜索
import bisect
import sys
# 在有序序列中用 bisect 查找某个元素的插入位置,不按下标,返回的是真正的位置,从1开始
num_list = [1, 3, 4, 5, 6, 7, 8, 9, 10]
find_num = 3
position = bisect.bisect(num_list, find_num)
print(position)
# 仿照书中例子
needles = [1, 11, 2, 4]
# 第一个格式化值(一个整数)应该输出为 2 位数字,如果不足则用前导零补全。例如,如果传入的值是 1,则输出为 01
# 第二个格式化值(也是一个整数)应该输出为 2 位数字,如果不足则用前导零补全。例如,如果传入的值为 5,则输出为 05
# {2} 是一个占位符,用于表示要替换的偏移量,用于在第一个占位符和第二个占位符之间打印分割符号。在实际使用时,偏移量由代码根据所需的空格数计算得出
# 最后一个占位符 {0:<2d} 表示第一个格式化值应该输出为左对齐的 2 位数字,并使用空格填充。例如,如果传入的值为 1,则输出为 1
ROW_FMT = '{0:2d} @ {1:2d} {2}{0:<2d}'
# 找位置打印
def test_func(bisect_fn):
# 倒序打印各needle
for needle in reversed(needles):
# 确定其位置
position = bisect_fn(num_list, needle)
# 添加分隔的标记
offset = position * ' |'
print(ROW_FMT.format(needle, position, offset))
if sys.argv[-1] == 'left':
bisect_fn = bisect.bisect_left
else:
bisect_fn = bisect.bisect
print('DEMO:', bisect_fn.__name__)
print('num ->', ' '.join('%2d' % n for n in num_list))
test_func(bisect_fn)
输出结果:
2
DEMO: bisect_right
num -> 1 3 4 5 6 7 8 9 10
4 @ 3 | | |4
2 @ 1 |2
11 @ 9 | | | | | | | | |11
1 @ 1 |1
bisect 函数其实是 bisect_right 函数的别名,后者还有个姊妹函数叫 bisect_left。它们的区别在于,bisect_left 返回的插入位置是原序列中跟被插入元素相等的元素的位置,也就是新元素会被放置于它相等的元素的前面,而 bisect_right 返回的则是跟它相等的元素之后的位置。
换成bisect_left:
import bisect
import sys
# 在有序序列中用 bisect 查找某个元素的插入位置,不按下标,返回的是真正的位置,从1开始
num_list = [1, 3, 4, 5, 6, 7, 8, 9, 10]
find_num = 3
position = bisect.bisect_left(num_list, find_num)
print(position)
# 仿照书中例子
needles = [1, 11, 2, 4]
# 第一个格式化值(一个整数)应该输出为 2 位数字,如果不足则用前导零补全。例如,如果传入的值是 1,则输出为 01
# 第二个格式化值(也是一个整数)应该输出为 2 位数字,如果不足则用前导零补全。例如,如果传入的值为 5,则输出为 05
# {2} 是一个占位符,用于表示要替换的偏移量,用于在第一个占位符和第二个占位符之间打印分割符号。在实际使用时,偏移量由代码根据所需的空格数计算得出
# 最后一个占位符 {0:<2d} 表示第一个格式化值应该输出为左对齐的 2 位数字,并使用空格填充。例如,如果传入的值为 1,则输出为 1
ROW_FMT = '{0:2d} @ {1:2d} {2}{0:<2d}'
# 找位置打印
def test_func(bisect_fn):
# 倒序打印各needle
for needle in reversed(needles):
# 确定其位置
position = bisect_fn(num_list, needle)
# 添加分隔的标记
offset = position * ' |'
print(ROW_FMT.format(needle, position, offset))
bisect_fn = bisect.bisect_left
print('DEMO:', bisect_fn.__name__)
print('num ->', ' '.join('%2d' % n for n in num_list))
test_func(bisect_fn)
运行结果:
1
DEMO: bisect_left
num -> 1 3 4 5 6 7 8 9 10
4 @ 2 | |4
2 @ 1 |2
11 @ 9 | | | | | | | | |11
1 @ 0 1
确实是这样,即返回的插入位置是原序列中跟被插入元素相等的元素的位置,这返回的是下标
根据旧十年假面骑士对应的年份找到其名字
# 根据旧十年假面骑士对应的年份找到其名字
import bisect
def get_rider_name(year
, rider_names=['Kuuga', 'Agito', 'Ryuki', 'Faiz', 'Blade', 'Hibiki', 'Kabuto', 'Den-o', 'Kiva', 'Decade']
, years=[2000,2001,2002,2003,2004,2005,2006,2007,2008,2009]):
i = bisect.bisect_left(years, year)
return rider_names[i]
print(get_rider_name(2000))
print(get_rider_name(2009))
运行结果:
Kuuga
Decade
用bisect.insort插入新元素
bisect.insort有序插入元素
import bisect
import random
# bisect.insort保持序列有序插入
l = [1, 2, 3]
# 插入一个随机数,有序插入
for i in range(0,10):
bisect.insort(l, random.randint(-10000, 10000))
print(l)
运行结果:
[-7968, -6609, -5859, -1062, 1, 2, 3, 2009, 5035, 5832, 6156, 7794, 9202]
数组
from array import array
from random import random
# 一个浮点型数组的创建、存入文件和从文件读取的过程
# 生成10个浮点数
floats = array('d', (random() for i in range(10 ** 7)))
print(floats[-1])
fp = open('floats.bin', 'wb')
# 使用 array.tofile 写入到二进制文件,
# 比以每行一个浮点数的方式把所有数字写入到文本文件要快 7倍。
floats.tofile(fp)
fp.close()
floats2 = array('d')
fp = open('floats.bin', 'rb')
# 用 array.fromfile 从一个二进制文件里读出 1000 万个双精度浮点数只需要 0.1 秒,
# 这比从文本文件里读取的速度要快60 倍,
# 因为后者会使用内置的 float 方法把每一行文字转换成浮点数。
floats2.fromfile(fp, 10**7)
fp.close()
print(floats[-1])
运行结果:
0.19028480838760442
0.19028480838760442
内存视图
这个玩意挺有意思,先说明一下,有符号整数占4个字节,一个字节是8位二进制(比特),而无符号整数占2个字节,有符号整数从左到右第一位二进制是符号位,1为负数,0位整数,后面是有效数字,有符号短整型占2个字节,其特性和有符号整型类似,只不过是2个字节限制,无符号字符型占1个字节。总而言之,无符号数没有符号位占位所以如果按字节存的话能比有符号数多一位二进制数,那么就出现了有意思的事情
import array
numbers = array.array('h', [-2, -1, 0, 1, 2])
# 利用含有 5 个短整型有符号整数的数组(类型码是 'h')创建一个 memoryview
memv = memoryview(numbers)
l = memv.tolist()
print(l)
print(memv[0])
# 转成无符号字符型
memv_oct = memv.cast('B')
l = memv_oct.tolist()
print(l)
输出结果:
[-2, -1, 0, 1, 2]
-2
[254, 255, 255, 255, 0, 0, 1, 0, 2, 0]
我们看到,数组变化了,这是为什么呢
我们将所有的数据转成二进制看看,计算机中都是以补码存储数据,这里补充一下原码,补码,反码的知识
对于有符号整数:
- 原码
原码就是符号位加上真值的绝对值, 即用第一位表示符号, 其余位表示值.- 反码
正数的反码是其本身
负数的反码是在其原码的基础上, 符号位不变,其余各个位取反.- 补码
补码的表示方法是:
正数的补码就是其本身
负数的补码是在其原码的基础上, 符号位不变, 其余各位取反, 最后+1. (即在反码的基础上+1)
P.S 无符号数就按其为正数算即可
P.S 补码的补码是原码
大小端模式
- 大端模式,是指数据的高字节保存在内存的低地址中,而数据的低字节保存在内存的高地址中,这样的存储模式有点儿类似于把数据当作字符串顺序处理:地址由小向大增加,数据从高位往低位放;这和我们的阅读习惯一致。
- 小端模式,是指数据的高字节保存在内存的高地址中,而数据的低字节保存在内存的低地址中,这种存储模式将地址的高低和数据位权有效地结合起来,高地址部分权值高,低地址部分权值低。
了解完这些,写个代码测试一下:
import array
import sys
numbers = array.array('h', [-2, -1, 0, 1, 2])
memv = memoryview(numbers)
l = memv.tolist()
# 给定原码,返回反码,number是存储二进制数字的字符串
# is_signed,True是有符号整数,False为无符号整数
def get_inverse_code(number, is_signed):
if number == "" or number is None:
raise ValueError("请输入有效的二进制数字符串!")
temp_str = ""
# 如果一个数是正数,反码和原码相同,负数则按位取反保留符号位
if number[0] == '0':
return number
# 无符号数的补码、反码、补码一致
if not is_signed:
return number
# 有符号数,则保留符号位进行转换,即从1到最后切片,第一位保留原第一位
temp_str += number[0]
# 如果长度大于1,才执行循环
if len(number) > 1:
for item in number[1:]:
if item == '0':
item = '1'
elif item == '1':
item = '0'
else:
item = " "
temp_str += item
return temp_str
# 给定原码,返回补码,number是存储二进制数字的字符串
def get_two_s_complement(number, is_signed):
if number == "" or number is None:
raise ValueError("请输入有效的二进制数字符串!")
# 正数的补码就是其本身
if is_signed == True and number[0] == '0':
return number
# 无符号数的补码、反码、补码一致
if not is_signed:
return number
# 先转成反码
icode = get_inverse_code(number, is_signed)
# 保存结果字符串
result = ""
# 对反码加1操作(1+1进位)
# 倒序遍历,从右向左加
is_carry = True # 上一次加法是否进位标志,因为要加1,肯定是最开始有进位(相当于加1)
for item in reversed(icode):
# 遇到1,如果上次运算没有进位,此位置还是1,不进位
if item == '1' and is_carry is False:
item = '1'
is_carry = False
# 遇到1,如果上次运算有进位,加1进位后,此位置变成0
elif item == '1' and is_carry is True:
item = '0'
is_carry = True
# 遇到0,如果上次运算没有进位,则还是0
elif item == '0' and is_carry is False:
item = '0'
is_carry = False
# 遇到0,如果上次运算有进位,此位置变成1
elif item == '0' and is_carry is True:
item = '1'
is_carry = False
# 其他情况为空格,不涉及改动进位标志
else:
item = ' '
result += item
# 倒置回去
result = result[::-1]
return result
# 根据十进制数(有符号)获取八位二进制数字符串,mode为字节数,比如4字节就选4
# 第一位为符号位
def get_signed_bin(dec_number, mode):
# 先判断一下当前字节数的最大值的二进制数是否能够放得下number
max_number = 0
# mode * 8 - 1 留出一个符号位
for i in range(0, mode * 8 - 1):
max_number += 2 ** i
if max_number < abs(dec_number):
raise ValueError("数值过大,建议增大字节数!")
# 存储结果的列表
result = []
# 存储下次运算待除的数
temp_number = abs(dec_number)
# 循环除2取余数,余数加入列表,余数即为二进制数(需要倒置)
is_eight = 0 # 八位计数器,如果已经算了八次,自动增加一个空格
# space_num记录已有的空格数
space_num = 0
while temp_number != 0:
result.append(str(temp_number % 2))
temp_number = temp_number // 2
is_eight += 1
# 如果不是最后一位二进制,并且还正好满8位,加一个空格
if is_eight == 8 and temp_number != 0:
result.append(' ')
space_num += 1
is_eight = 0 # 满8清零一次,最后一次不清零
# 生成二进制后,进行补0操作
# 如果列表长度小于字节数mode * 8 + (mode - 1),mode-1是指中间的空格数
# 则说明需要补0,否则不补0,补0留出一个符号位
if len(result) < (mode * 8 + (mode - 1)):
# 需要补mode * 8 + (mode - 1) - len(result) - 1个0或空格(因为要留出符号位)
# 即补齐连带格式化输出空格的字符串的字符数
for i in range(0, mode * 8 + (mode - 1) - len(result) - 1):
# 检测生成二进制的时候,is_eight是否到8,到8则补空格
if is_eight == 8:
result.append(' ')
is_eight = 0
else:
result.append('0')
is_eight += 1
# 确定符号位,1负,0正
if dec_number >= 0:
result.append('0')
else:
result.append('1')
result.reverse()
return "".join(result)
# 获取无符号10进制转二进制后的字符串
def get_unsigned_bin(dec_number, mode):
# 先判断一下当前字节数的最大值的二进制数是否能够放得下number
max_number = 0
for i in range(0, mode * 8):
max_number += 2 ** i
if max_number < abs(dec_number):
raise ValueError("数值过大,建议增大字节数!")
# 存储结果的列表
result = []
# 存储下次运算待除的数
temp_number = abs(dec_number)
# 循环除2取余数,余数加入列表,余数即为二进制数(需要倒置)
is_eight = 0 # 八位计数器,如果已经算了八次,自动增加一个空格
while temp_number != 0:
result.append(str(temp_number % 2))
temp_number = temp_number // 2
is_eight += 1
# 如果不是最后一位二进制,并且还正好满8位,加一个空格
if is_eight == 8 and temp_number != 0:
result.append(' ')
is_eight = 0 # 满8清零一次,最后一次不清零
# 生成二进制后,进行补0操作
# 如果列表长度小于字节数mode * 8 + (mode - 1),mode-1是指中间的空格数
# 则说明需要补0,否则不补0,无需留出符号位
print(result)
print(len(result))
if len(result) < (mode * 8 + (mode - 1)):
# 需要补mode * 8 + (mode - 1) - len(result)个0或空格(不需要留出符号位)
for i in range(0, mode * 8 + (mode - 1) - len(result)):
# 检测生成二进制的时候,is_eight是否到8,到8则补空格,最后一次不补空格
if is_eight == 8:
result.append(' ')
is_eight = 0
else:
result.append('0')
is_eight += 1
result.reverse()
return "".join(result)
# 根据补码生成原码,is_signed表示是否是符号数
def t_to_number(number, is_signed):
if number == "" or number is None:
raise ValueError("请输入有效的二进制数字符串!")
# 正数的原码和补码一样
if is_signed == True and number[0] == '0':
return number
# 将二进制转为十进制
def get_bin_to_dec(number):
index = 0 # 二进制数字字符串的下标
result = 0 # 保存转换结果
# 倒着遍历,从右往左
for item in reversed(number):
if item == '1':
result += 2 ** index
index += 1
return result
# 确认以下当前计算机的大小端模式
print("当前计算机的大小端模式为:")
big_or_l = str(sys.byteorder)
if big_or_l == 'little':
print("小端存储")
else:
print("大端存储")
print()
for number in l:
print("十进制:" + str(number))
bin_str = get_signed_bin(number, 2)
print("从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)")
print("有符号短整型二进制整数(2字节):" + bin_str)
print("反码:" + get_inverse_code(bin_str, True))
print("补码:" + get_two_s_complement(bin_str, True))
# 按字节分开
l_str = get_two_s_complement(bin_str, True).split()
# 前两个字节合成一个无符号数的补码
print("将其以无符号字符型读入变成两个无符号字符,其中补码分别为:")
x1_t = str(l_str[0])
x2_t = str(l_str[1])
print(x1_t+" ", end="")
print(x2_t)
print("按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):")
print("无符号类型的原码、补码、反码是一致的")
x1 = get_two_s_complement(x1_t, False)
x2 = get_two_s_complement(x2_t, False)
print(x1+" ", end="")
print(x2)
print("转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):")
print(get_bin_to_dec(x1))
print(get_bin_to_dec(x2))
print()
运行结果
当前计算机的大小端模式为:
小端存储
十进制:-2
从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)
有符号短整型二进制整数(2字节):10000000 00000010
反码:11111111 11111101
补码:11111111 11111110
将其以无符号字符型读入变成两个无符号字符,其中补码分别为:
11111111 11111110
按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):
无符号类型的原码、补码、反码是一致的
11111111 11111110
转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):
255
254
十进制:-1
从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)
有符号短整型二进制整数(2字节):10000000 00000001
反码:11111111 11111110
补码:11111111 11111111
将其以无符号字符型读入变成两个无符号字符,其中补码分别为:
11111111 11111111
按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):
无符号类型的原码、补码、反码是一致的
11111111 11111111
转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):
255
255
十进制:0
从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)
有符号短整型二进制整数(2字节):00000000 00000000
反码:00000000 00000000
补码:00000000 00000000
将其以无符号字符型读入变成两个无符号字符,其中补码分别为:
00000000 00000000
按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):
无符号类型的原码、补码、反码是一致的
00000000 00000000
转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):
0
0
十进制:1
从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)
有符号短整型二进制整数(2字节):00000000 00000001
反码:00000000 00000001
补码:00000000 00000001
将其以无符号字符型读入变成两个无符号字符,其中补码分别为:
00000000 00000001
按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):
无符号类型的原码、补码、反码是一致的
00000000 00000001
转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):
0
1
十进制:2
从右往左二进制位数增高(低位在右侧,按小端存储,先读右侧)
有符号短整型二进制整数(2字节):00000000 00000010
反码:00000000 00000010
补码:00000000 00000010
将其以无符号字符型读入变成两个无符号字符,其中补码分别为:
00000000 00000010
按照补码的补码是原码原则,分别将其转为原码(按无符号数的规则):
无符号类型的原码、补码、反码是一致的
00000000 00000010
转为10进制为(按小端存储先读右侧,从右往左读,低位在下侧):
0
2
数组占用是一片连续存储的内存空间,按输出结果画一个内存逻辑图清晰可见:
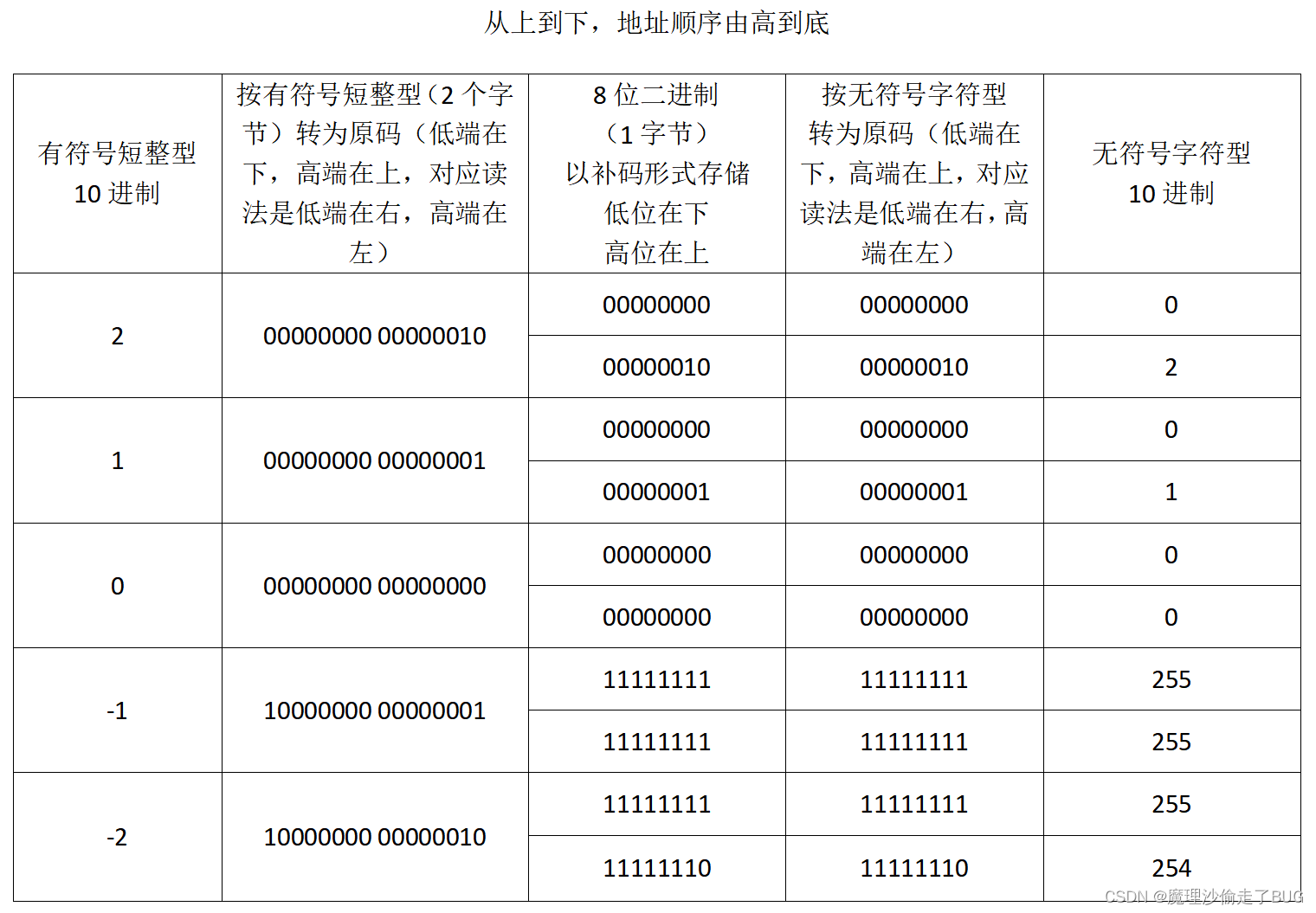
按照计算机的方式,如果按有符号短整型进行读取,从低地址(下侧)到高地址(上侧)读是数组[-2, -1, 0, 1, 2],但是如果按无符号字符型读则为[254, 255, 255, 255, 0, 0, 1, 0, 2, 0]
我们按有符号短整型修改其中的一个值:
import array
numbers = array.array('h', [-2, -1, 0, 1, 2])
memv = memoryview(numbers)
l = memv.tolist()
print(l)
memv_oct = memv.cast('B')
print(memv_oct.tolist())
# 按无符号字符型将下标为5位置的值赋值为4
memv_oct[5] = 4
# 按有符号短整型遍历数组
print(numbers)
运行结果:
[-2, -1, 0, 1, 2]
[254, 255, 255, 255, 0, 0, 1, 0, 2, 0]
array(‘h’, [-2, -1, 1024, 1, 2])
也就相当于如下的内存逻辑图:
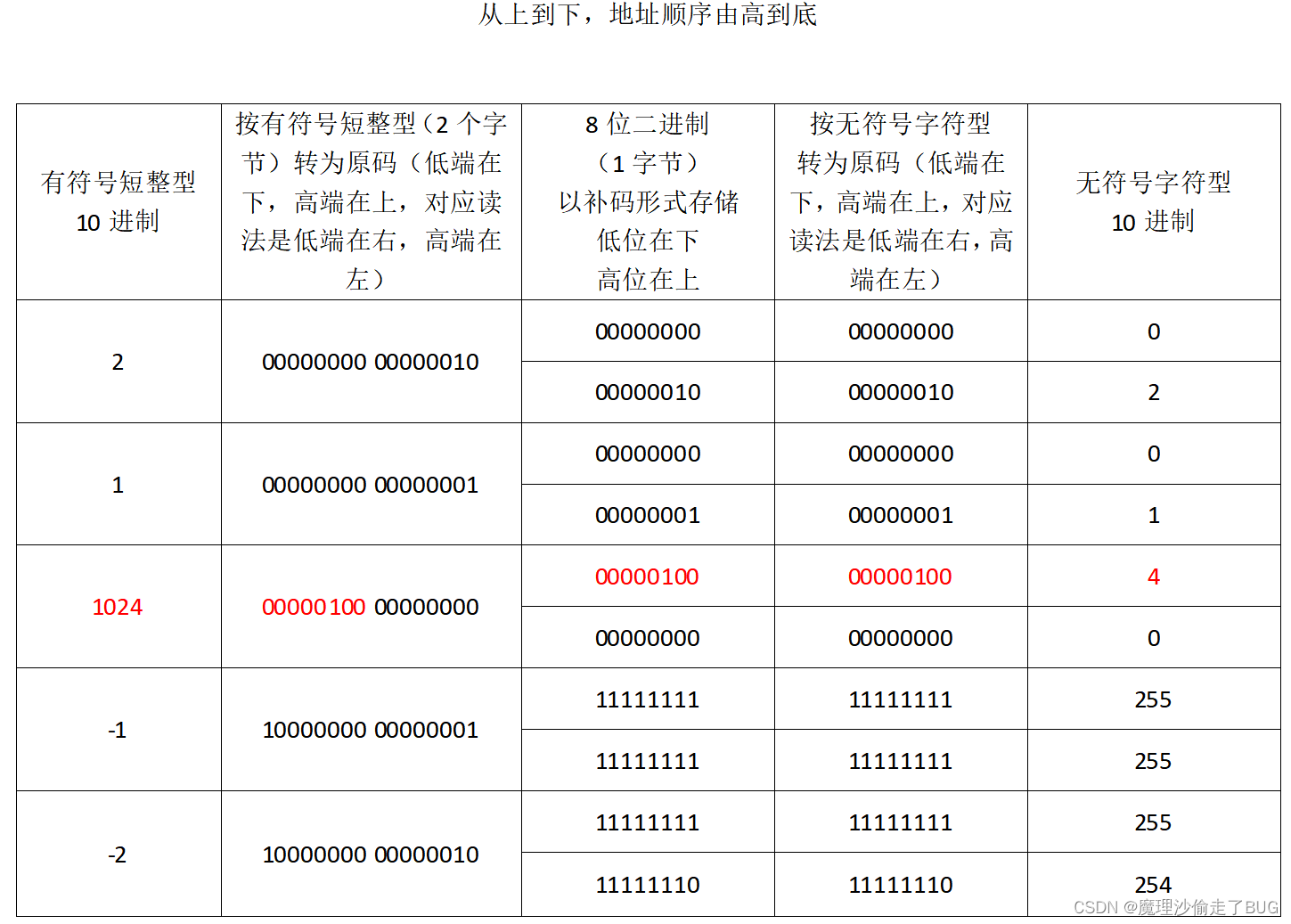
这样再用有符号短整型打印,就会看到下标为2的位置变为1024
NumPy和SciPy
书中简略介绍了一下这两个库,其实这两个库作用蛮大的
简单试试,以前常用,不细说了
import numpy
a = numpy.arange(12)
print(a)
print(a.shape)
a.shape = 3, 4
print(a)
# 打印下标为1的列
print(a[:, 1])
# 打印下标为1的行
print(a[1, :])
# 取a的转置,多维才有效果
print(a.transpose())
运行结果:
[ 0 1 2 3 4 5 6 7 8 9 10 11]
(12,)
[[ 0 1 2 3]
[ 4 5 6 7]
[ 8 9 10 11]]
[1 5 9]
[4 5 6 7]
[[ 0 4 8]
[ 1 5 9]
[ 2 6 10]
[ 3 7 11]]
双向队列和其他形式的队列
collections.deque 类(双向队列)是一个线程安全、可以快速从两端添加或者删除元素的数据类型。而且如果想要有一种数据类型来存放“最近用到的几个元素”,deque 也是一个很好的选择。
from collections import deque
dq = deque(range(10), maxlen=10)
print(dq)
# 队列旋转
# 队列的旋转操作接受一个参数 n,
# 当 n > 0 时,队列的最右边的 n 个元素会被移动到队列的左边。
# 当 n < 0 时,最左边的 n 个元素会被移动到右边。
dq.rotate(3)
print(dq)
dq.rotate(-3)
print(dq)
# 队列一共长度为10,队中元素为10,队列已经满了,如果从左侧入队,那么会替换掉左侧第一个元素
dq.appendleft(-1)
print(dq)
# 在尾部添加 3 个元素的操作会挤掉最左侧三个元素,因为队列已满
# 相当于往左移动
dq.extend([11, 22, 33])
print(dq)
# extendleft(iter) 方法会把迭代器里的元素逐个添加到双向队列的左边,因此迭代器里的元素会逆序出现在队列里
# 因为队列已满
# 相当于往右移动
dq.extendleft([100, 200, 300])
print(dq)
运行结果:
deque([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], maxlen=10)
deque([7, 8, 9, 0, 1, 2, 3, 4, 5, 6], maxlen=10)
deque([0, 1, 2, 3, 4, 5, 6, 7, 8, 9], maxlen=10)
deque([-1, 0, 1, 2, 3, 4, 5, 6, 7, 8], maxlen=10)
deque([2, 3, 4, 5, 6, 7, 8, 11, 22, 33], maxlen=10)
deque([300, 200, 100, 2, 3, 4, 5, 6, 7, 8], maxlen=10)