问题引入

二分查找的思路

二分查找的实现

左闭右闭写法

左闭右开写法

两种写法的对比

例题强化

常规的二分查找题目

猜数字大小

搜索插入位置

常规二分的变形题目

搜索二维矩阵

搜索二维矩阵 II

查找特定位置/特定数

在排序数组中查找元素的第一个和最后一个位置

寻找旋转排序数组种的最小值

寻找旋转排序数组中的最小值 II

搜索旋转排序数组

不在同一个数组的二分

寻找两个正序数组的中位数

最后

问题引入

还记得在初中或者高中的时候就知道二分查找这个东西了，当时理解起来也不难，感觉挺简单的。后来在编程学习中也遇到了二分查找，刚开始觉得这是一个初高中就会的东西，也就没太重视。但到了编程实现的时候就不是那么回事了，边界问题很难处理好，换了问题模型就无从下手。可见，在学习过程中保持空杯心态还是很重要的。所以要把二分查找的问题整理成一篇博客总结下来。

第一次接触二分查找的问题是一个“猜数字”的游戏，大体意思就是：小红心里想一个数字，小明去猜这个数字是多少，猜对了小红就奖励他，猜错了就再猜，直到猜中为止其中如果猜的数大于小红心里想的数，小红就说大了，反之就说小了，问小明怎么猜才最快。然后聪明的小明就想到了，先从最中间的数开始猜，不论是大了还是小了，小明都可以排除掉一半的数，这样最坏的情况也只需要7次就可以得到小红的奖励了。而这种每次折半查找的方式就叫做二分查找。

二分查找的思路

把上述的“猜数字”游戏具象化就是：设有一个有序升序数组nums，其中存放的是1-100这100个数，我们需要在这个数组中查找目标值target。那么对应的我们需要设一个left和right变量，left表示我们所要查找区间的左边界，right为右边界，还需要一个mid变量表示left和right的中间位置。然后我们将nums[mid]与目标值target进行对比，如果这两者恰好相等，那么说明此时的mid位置就是我们需要找的数。否则，如果nums[mid]大于target，那么就将left和right的范围向左缩进(折半)，那么就让right跑到mid的位置，随之更新mid，再重复上述操作，直至left与right“相撞”表示当前数组已经查找完了，说明nums中没有target。

总结一下就是，二分查找又叫折半查找，思路很好理解，就是每次从指定范围内进行查找(这个范围内的数都是有序的)，如果找到了就结束，没找到就根据当前范围内中间位置的数与要找的数对比，并将原范围折半缩小，这样每次就可以排除掉当前范围一半的数据。所以二分查找的次数就是logN次，即二分查找的时间复杂度为O(logN)。

二分查找的实现

二分的思路很好理解，但二分查找的实现并不是很好把控的。二分查找常见写法的有两种，分别是左闭右闭和左闭右开。

左闭右闭写法

对于左闭右闭写法，数学形式表示就是 [left,right] 说明当前锁定的范围是包含left和right下标位置及它们之间的数据。例如对于数组nums（数据刚好等于下标）

nums：0 1 2 3 4 5 6 7 8 9

如果left为2，right为5，那么就相当于

nums：0 1 [ 2 3 4 5 ] 6 7 8 9

即我们当前锁定的范围就是 [ 2 3 4 5 ] 。那么我们就可以根据这个特性来控制循环条件，进而进行二分查找，即

while(left <= right)

如果你还不明白为什么要这样写，这里可以再啰嗦一些。由于左闭右闭写法的区间为 [left,right] 那么当left=right时，就相对于目前锁定的范围中只有一个数。例如对于上方的数组nums，那么如果left=right=3，那么就相当于

nums：0 1 2 [ 3 ] 4 5 6 7 8 9

那么当不满足 left <= right 时，left = right-1，如果此时left还是3的话，那么对应的right就是2，就相当于

nums：0 1 2 ] [ 3 4 5 6 7 8 9

如果此时我们二分查找的数是3的话，那么当循环结束时对应的left和right就是上面那个样子，target（要查找的数字3）所对应的下标就是left（right位置的是2）

代码实现如下：

//nums是一个升序数组，n是nums数组的长度，target是要查找的目标值
int BinarySearch(int* nums, int n, int target) 
{
    int left = 0, right = n - 1;
    while(left <= right) 
    {
        //这里的mid写成：int mid = left + (right - left) / 2; 的效果更好
        //因为left直接与right相加可能会出现int数据溢出的情况
        //但为了更好理解还是暂定写成下面的形式
        int mid = (left + right) / 2;   
    
        //mid位置的数大于target
        if (nums[mid] > target) 
            right = mid - 1; 

        //mid位置的数小于target
        else if (nums[mid] < target) 
            left = mid + 1 ;

        //mid位置的数等于target
        else 
            return mid;
    }
    return -1;
}

这里还需要解释一下代码中的一些细节问题，对于mid的写法代码注释中已经说明了这里就不再过多赘述。而对于 left = mid + 1 和 right = mid - 1，我们以后者（ right = mid - 1）为例进行解释。当mid位置的大于target，那么说明mid位置的数是大于target（当然，这是一句废话），并且它右边的数都是大于target的，所以可以直接把mid及其右边的数直接排除，将锁定的范围更新为 [left,mid - 1] （简言之，此时的mid已经被排除了），由于这是左闭右闭的写法，那么right可以直接等同于mid-1。left的情况也是同理。

左闭右开写法

清楚了左闭右闭是怎么一回事，那么左闭右开就表示 [left,right) ，就是说当前锁定的范围并不包含right，也可以理解为锁定范围的内容就相当于 [left, right-1] 。

我们还是以上面的nums数组为例，如果left为2，right为5，那么就相当于（蓝色的表示right-1）

nums：0 1 [ 2 3 4 ] 5 ) 6 7 8 9

那么控制循环的条件就变成了

while(letf < right)

其实也不难理解，left < right 就相对于 left <= right-1，即结束循环时left=right。还是设我们要找的target是3，那么最后的结果left=right=3，就相对于（蓝色的表示right-1）

nums：0 1 2 ] [ 3 ) 4 5 6 7 8 9

所以，一般来说这与左闭右闭写法产生的效果是一样的。

有了上面的基础，那么对应的代码也就不难理解了。

int BinarySearch(int* nums, int n, int target) 
{
    int left = 0, right = n - 1;
    while(left < right) 
    {
        int mid = left + (right - left) / 2; 
        if (nums[mid] > target) 
            right = mid; 
        else if (nums[mid] < target) 
            left = mid + 1 ;
        else 
            return mid;
    }
    return -1;
}

这段代码与上面的代码基本上没有什么区别，只是循环条件变成了left<right（原因已经在上面阐释过了）。还有一点就是当nums[mid] > target 的时候变成了 right = mid 。这是因为这里的区间控制是 [left,right)，虽然此时的有效范围是 [left,mid-1] 但由于 [left,right) 范围并不包含right，所以这里的有效范围就相当于 [left,right-1] ，或者也可以理解为 [left,mid) 。但不管是从哪种角度来理解，对应的right就相当于mid，它们是不包含在有效范围内的，right-1就相当于mid-1，它们是包含在有效范围内的。如果这里用的是right=mid-1，那么就会出现遗漏数据的情况。

两种写法的对比

1、两种写法代码实现上基本上差不多，只有两处需要注意，循环条件上：左闭右闭的是while(left<=right)，而左闭右开的是while(left<right)。right左移上：左闭右闭的是right=mid-1，而左闭右开的是right=mid。

2、左闭右闭和左闭右开虽然在写法上有所出入，但最终所达到的效果是差不多的。那么有人就会问了，既然两个效果都差不多，那么为什么还要有下面这种左闭右开的写法呢，全都用左闭右闭不久好了，何必如此鸡肋。其实不然，世间万物存在一定都有它的意义，虽然在一般情况下两种写法都差不多，但在一些特定的问题处理上，有时只能用左闭右开或者只能用左闭右闭的情况。

3、其实二分的范围控制不是只有这两种，也可以写成左开右开或者左开右闭的情形，但这两种情形对应的应用场景很少，而且用起来很麻烦，所以基本上是不会用到的。

例题强化

二分查找的难点不在于理解，而在于应用，下面我们通过几组例题循序渐进的强化我们对二分查找的把控能力（题目均选自力扣-leetcode ）

常规的二分查找题目

猜数字大小

374. 猜数字大小 - 题目链接https://leetcode.cn/problems/guess-number-higher-or-lower/

题目描述：

猜数字游戏的规则如下：

每轮游戏，我都会从 1 到 n 随机选择一个数字。请你猜选出的是哪个数字。如果你猜错了，我会告诉你，你猜测的数字比我选出的数字是大了还是小了。你可以通过调用一个预先定义好的接口 int guess(int num) 来获取猜测结果返回值一共有 3 种可能的情况（-1，1 或 0）：

-1：我选出的数字比你猜的数字小 pick < num
1：我选出的数字比你猜的数字大 pick > num
0：我选出的数字和你猜的数字一样。恭喜！你猜对了！pick == num 返回我选出的数字。

示例 1：
输入：n = 10, pick = 6
输出：6

示例 2：
输入：n = 1, pick = 1
输出：1

示例 3：
输入：n = 2, pick = 1
输出：1

示例 4：
输入：n = 2, pick = 2
输出：2

提示：
1 <= n <= 231 - 1
1 <= pick <= n
1 <= n <= 231 - 1
1 <= pick <= n

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/guess-number-higher-or-lower
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：这题与文章开头小红和小明的例子相差无几，这里就直接贴题解代码了。

参考题解：

/** 
 * Forward declaration of guess API.
 * @param  num   your guess
 * @return 	     -1 if num is higher than the picked number
 *			      1 if num is lower than the picked number
 *               otherwise return 0
 * int guess(int num);
 */

class Solution {
public:
    int guessNumber(int n) 
    {
        int left = 0, right = n;
        while(left <= right)
        {
            int mid = left + (right - left) / 2;
            if(guess(mid) == 0)
                return mid;
            else if(guess(mid) < 0)
                right = mid - 1;
            else
                left = mid + 1;
        }
        return 0;
    }
};

搜索插入位置

35. 搜索插入位置https://leetcode.cn/problems/search-insert-position/

题目描述：

给定一个排序数组和一个目标值，在数组中找到目标值，并返回其索引。
如果目标值不存在于数组中，返回它将会被按顺序插入的位置。

请必须使用时间复杂度为 O(log n) 的算法。

示例 1:
输入: nums = [1,3,5,6], target = 5
输出: 2

示例 2:
输入: nums = [1,3,5,6], target = 2
输出: 1

示例 3:
输入: nums = [1,3,5,6], target = 7
输出: 4

提示:
1 <= nums.length <= 104
-104 <= nums[i] <= 104
nums 为无重复元素的升序排列数组
-104 <= target <= 104

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-insert-position
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：要注意理解好题目中的“返回它将会被按顺序插入的位置”，其实说白了就是对这个数组进行二分，然后返回对应的left或者mid值（左闭右闭的情况），因为如果target不在有序数组nums中的话，二分之后的left就是第一个大于target的数的位置。我们通过“示例2”来感受一下，

输入: nums = [1,3,5,6], target = 2

输出: 1

首先，如果nums = [1,2,3,5,6] 的输出还是1吗？答案是，是的。对应结果如下

1 ][ 2 3 5 6

所以如果把2去掉之后那么最后的left和right位置还是在那个地方，相当于把2移走了，那么left位置的元素自然就变成了3。

所以最终二分的结果就是下面这种，二分最后的left=1，right=0。可以看到，这时的left位置恰好为target（就是2）插入之后的位置。

nums： 1 ] [ 3 5 6

参考题解：

class Solution {
public: 
    int searchInsert(vector<int>& nums, int target) 
    { 
        int left = 0, right = nums.size() - 1; 
        while(left <= right) 
        { 
            int mid = left + (right - left) / 2;
            if(nums[mid] == target)
                return mid;
            else if(nums[mid] > target)
                right = mid - 1;
            else
                left = mid + 1;
        } 
        return left;
    }
};

常规二分的变形题目

搜索二维矩阵

74. 搜索二维矩阵https://leetcode.cn/problems/search-a-2d-matrix/

题目描述：

编写一个高效的算法来判断 m x n 矩阵中，是否存在一个目标值。该矩阵具有如下特性：

每行中的整数从左到右按升序排列。
每行的第一个整数大于前一行的最后一个整数。

示例 1：

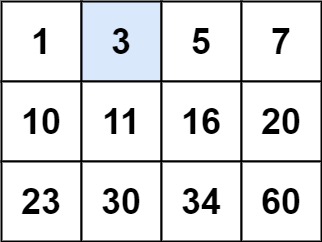
leetcode官方图

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 3
输出：true
示例 2：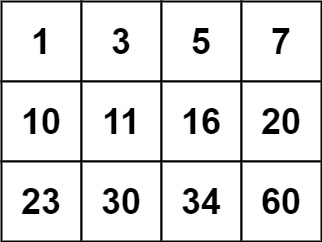

leetcode官方图

输入：matrix = [[1,3,5,7],[10,11,16,20],[23,30,34,60]], target = 13
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= m, n <= 100
-104 <= matrix[i][j], target <= 104

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

这题是一个很常规的二分加了一点变化，由于这个矩阵比较特殊，很容易想到利用两次二分，先对每行的第一个数进行二分，找到第一个大于target所在的行row，然后对row-1行再进行一次二分，最终结果就是我们所要的结果。还有一种思路就是把这个二维数组的每一行合并成一个一维数组，然后对这个一维数组进行二分。这两种思路的时间复杂度都是O(logMN)

参考题解：

这里用的是两次二分的思路，如果觉得第一个代码理解起来稍复杂可以看下面手动二分的版本。

//写法1，直接利用内置算法
class Solution {
public:
    bool searchMatrix(vector<vector<int>> matrix, int target) 
    {
        //找到第一个首行大于target的行数
        auto row = upper_bound(matrix.begin(), matrix.end(), target,
                    [](const int tag, const vector<int>& matrixRow)
                    {
                        return tag < matrixRow[0];
                    } );
        //如果tag小于matrix[0][0]，直接返回false
        if(row == matrix.begin())
            return false;
        //对row-1行进行二分
        row--;
        return binary_search(row->begin(), row->end(), target);
    }
};

//写法2，自己手动二分
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) 
    {
        //解法2：两次二分,时间复杂度 O(logN + logN) = O(logMN)
        //找符合条件的行
        int left1 = 0, right1 = matrix.size() - 1;
        while(left1 <= right1)
        {
            int mid = left1 + (right1 - left1) / 2; 
            if(matrix[mid][0] == target)
                return true;
            else if(matrix[mid][0] > target)
                right1 = mid - 1;
            else    
                left1 = mid + 1;
        } 
        //如果tag小于matrix[0][0]，直接返回false   
        if(right1 < 0) 
            return false;
        cout<<right1<<endl;
        cout<<matrix[right1][0]<<endl;
        //对可能的行进行二分
        int left2 = 0, right2 = matrix[0].size() - 1;
        while(left2 <= right2)
        {
            int mid = left2 + (right2 - left2) / 2;
            if(matrix[right1][mid] == target) 
                return true;
            else if(matrix[right1][mid] > target)
                right2 = mid - 1;
            else    
                left2 = mid + 1;
        }
        return false;
    }
};

搜索二维矩阵 II

240. 搜索二维矩阵 IIhttps://leetcode.cn/problems/search-a-2d-matrix-ii/

题目描述：

编写一个高效的算法来搜索 m x n 矩阵 matrix 中的一个目标值 target 。该矩阵具有以下特性：

每行的元素从左到右升序排列。
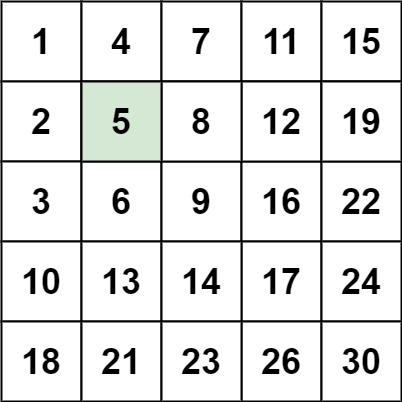
每列的元素从上到下升序排列。

示例 1：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 5
输出：true
示例 2：

输入：matrix = [[1,4,7,11,15],[2,5,8,12,19],[3,6,9,16,22],[10,13,14,17,24],[18,21,23,26,30]], target = 20
输出：false

提示：

m == matrix.length
n == matrix[i].length
1 <= n, m <= 300
-109 <= matrix[i][j] <= 109
每行的所有元素从左到右升序排列
每列的所有元素从上到下升序排列
-109 <= target <= 109

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-a-2d-matrix-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：乍一看这题和“搜索二维矩阵”好像没什么区别，所以小白上来直接把“搜索二维矩阵”的代码给提交上去了，结果可想而知的报错了。这题与“搜索二维矩阵”的一个不同之处就在于这题的矩阵层与层之间没有必然的联系，所以上一题的“两次二分”与“合并+一次二分”的思路在这里就行不通了。这题的一个二分解法是对每一行进行二分，寻找两个正序数组的中位数复杂度为O(MlogN)。当然这题用二分并不是最好的解法，还有一个很妙的 “Z字形查找” 的思路。但由于这里是以讲解二分为主，所以就不展开说这个 “Z字形查找”了，感兴趣的可以看一下题解部分的第二个代码。

参考题解：

//m次二分
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) {
        for (const auto& row: matrix) {
            auto it = lower_bound(row.begin(), row.end(), target);
            if (it != row.end() && *it == target) {
                return true;
            }
        }
        return false;
    }
};

//Z字查找
class Solution {
public:
    bool searchMatrix(vector<vector<int>>& matrix, int target) 
    {
        int m = 0, n = matrix[0].size() - 1; //m-行，n-列
        while(m < matrix.size() && n > -1)
        {
            if(matrix[m][n] == target)
                return true;
            else if(matrix[m][n] > target)
                n--;
            else
                m++;
        }
        return false;
    }
};

查找特定位置/特定数

在排序数组中查找元素的第一个和最后一个位置

34. 在排序数组中查找元素的第一个和最后一个位置https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array/

题目描述：

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。

如果数组中不存在目标值 target，返回 [-1, -1]。

你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [5,7,7,8,8,10], target = 8
输出：[3,4]

示例 2：

输入：nums = [5,7,7,8,8,10], target = 6
输出：[-1,-1]

示例 3：

输入：nums = [], target = 0
输出：[-1,-1]

提示：

0 <= nums.length <= 105
-109 <= nums[i] <= 109
nums 是一个非递减数组
-109 <= target <= 109

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-first-and-last-position-of-element-in-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

参考题解：

//写法1：
class Solution {
public:
    int searchFirst(vector<int>& nums, int target)
    {
        if(nums.empty())
            return -1;
        int left = 0, right = nums.size() - 1, mid = 0;
        //控制区间是 [left,right] 而不是 [left,right)
        while(left <= right) 
        {
            //防止范围过大导致int溢出
            mid = left + (right - left) / 2; 
            if(nums[mid] == target)
                right = mid - 1;
            else if(nums[mid] > target)
                right = mid - 1;
            else
                left = mid + 1;
        }
        return left;
    }
    int searchEnd(vector<int>& nums, int target)
    {
        if(nums.empty())
            return -1; 
        int left = 0, right = nums.size() - 1, mid = 0;
        while(left <= right) 
        {
            mid = left + (right - left) / 2; 
            if(nums[mid] == target)
                left = mid + 1;
            else if(nums[mid] > target)
                right = mid - 1;
            else
                left = mid + 1;
        }
        return right;
    }
    vector<int> searchRange(vector<int>& nums, int target)  
    {
        int first = searchFirst(nums, target); 
        int end = searchEnd(nums, target); 
        if(first > end)
            return vector{-1, -1}; 
        return vector{first, end}; 
    }
};

//写法2：
class Solution {
public:
    int searchEnd(vector<int>& nums, int target)
    {
        if(nums.empty())
            return -1; 
        int left = 0, right = nums.size() - 1, mid = 0;
        while(left <= right) 
        {
            mid = left + (right - left) / 2; 
            if(nums[mid] == target)
                left = mid + 1;
            else if(nums[mid] > target)
                right = mid - 1;
            else
                left = mid + 1;
        }
        return left;
    }
    vector<int> searchRange(vector<int>& nums, int target)  
    {
        int first = searchEnd(nums, target - 1);
        int end = searchEnd(nums, target) - 1;
        if(first > end)
            return vector{-1, -1};
        return vector{first, end};
    }
};

寻找旋转排序数组种的最小值

153. 寻找旋转排序数组中的最小值https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array/

题目描述：

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,2,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,2]
若旋转 7 次，则可以得到 [0,1,2,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个元素值互不相同的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [3,4,5,1,2]
输出：1
解释：原数组为 [1,2,3,4,5] ，旋转 3 次得到输入数组。

示例 2：

输入：nums = [4,5,6,7,0,1,2]
输出：0
解释：原数组为 [0,1,2,4,5,6,7] ，旋转 4 次得到输入数组。

示例 3：

输入：nums = [11,13,15,17]
输出：11
解释：原数组为 [11,13,15,17] ，旋转 4 次得到输入数组。

提示：

n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 中的所有整数互不相同
nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

参考题解：

class Solution {
public:
    int findMin(vector<int>& nums) 
    
    {
        int left = 0;
        int right = nums.size() - 1;
        //前闭后开的写法
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] > nums[right])
                left = mid + 1;
            else
                right = mid;
        }
        return nums[right];
    }
};

寻找旋转排序数组中的最小值 II

154. 寻找旋转排序数组中的最小值 IIhttps://leetcode.cn/problems/find-minimum-in-rotated-sorted-array-ii/

题目描述：

已知一个长度为 n 的数组，预先按照升序排列，经由 1 到 n 次旋转后，得到输入数组。例如，原数组 nums = [0,1,4,4,5,6,7] 在变化后可能得到：
若旋转 4 次，则可以得到 [4,5,6,7,0,1,4]
若旋转 7 次，则可以得到 [0,1,4,4,5,6,7]
注意，数组 [a[0], a[1], a[2], ..., a[n-1]] 旋转一次的结果为数组 [a[n-1], a[0], a[1], a[2], ..., a[n-2]] 。

给你一个可能存在重复元素值的数组 nums ，它原来是一个升序排列的数组，并按上述情形进行了多次旋转。请你找出并返回数组中的最小元素。

你必须尽可能减少整个过程的操作步骤。

示例 1：

输入：nums = [1,3,5]
输出：1

示例 2：

输入：nums = [2,2,2,0,1]
输出：0

提示：

n == nums.length
1 <= n <= 5000
-5000 <= nums[i] <= 5000
nums 原来是一个升序排序的数组，并进行了 1 至 n 次旋转

进阶：这道题与寻找旋转排序数组中的最小值类似，但 nums 可能包含重复元素。允许重复会影响算法的时间复杂度吗？会如何影响，为什么？

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/find-minimum-in-rotated-sorted-array-ii
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

参考题解：

class Solution {
public:
    int findMin(vector<int>& nums) 
    
    {
        int left = 0;
        int right = nums.size() - 1;
        //前开后开的写法
        while(left < right)
        {
            int mid = left + (right - left) / 2;
            if(nums[mid] > nums[right])
                left = mid + 1;
            else if(nums[mid] < nums[right])
                right = mid;
            else
                right--;
        }
        return nums[right];
    }
};

搜索旋转排序数组

33. 搜索旋转排序数组https://leetcode.cn/problems/search-in-rotated-sorted-array/

题目描述：

整数数组 nums 按升序排列，数组中的值互不相同。

在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标从 0 开始计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处经旋转后可能变为 [4,5,6,7,0,1,2] 。

给你旋转后的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

示例 1：

输入：nums = [4,5,6,7,0,1,2], target = 0
输出：4

示例 2：

输入：nums = [4,5,6,7,0,1,2], target = 3
输出：-1

示例 3：

输入：nums = [1], target = 0
输出：-1

提示：

1 <= nums.length <= 5000
-104 <= nums[i] <= 104
nums 中的每个值都独一无二
题目数据保证 nums 在预先未知的某个下标上进行了旋转
-104 <= target <= 104

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/search-in-rotated-sorted-array
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

参考题解：

class Solution {
public:
    int search(vector<int>& nums, int target) 
    {
        int left = 0, right = nums.size() - 1;
        int mid = 0;
        while(left <= right)
        {
            //更新mid值
            mid = (left + right) / 2;
            //查找到就返回
            if(nums[mid] == target)
                return mid;     
            //0-mid范围内为有序正常二分的情况，按照二分的情况正常处理
            else if(nums[0] <= nums[mid]) //无重复元素，所以这样用
            {
                if(nums[mid] > target && target >= nums[0]) //严格控制区间
                    right = mid - 1;
                else
                    left = mid + 1;
            }
            //0-mid范围内为乱序旋转序列的情况，需要根据target的位置按情况处理 
            else/*此情况下mid一定是在乱序数组的中间*/
            {
                //target在mid右边，向右缩进
                if(nums[mid] < target && target <= nums[nums.size()-1])
                    left = mid + 1;           
                else           
                    right = mid - 1;
            }      
        }
        return -1;
    }
};

不在同一个数组的二分

寻找两个正序数组的中位数

4. 寻找两个正序数组的中位数https://leetcode.cn/problems/median-of-two-sorted-arrays/

题目描述：

给定两个大小分别为 m 和 n 的正序（从小到大）数组 nums1 和 nums2。请你找出并返回这两个正序数组的中位数。

算法的时间复杂度应该为 O(log (m+n)) 。

示例 1：

输入：nums1 = [1,3], nums2 = [2]
输出：2.00000
解释：合并数组 = [1,2,3] ，中位数 2

示例 2：

输入：nums1 = [1,2], nums2 = [3,4]
输出：2.50000
解释：合并数组 = [1,2,3,4] ，中位数 (2 + 3) / 2 = 2.5

提示：

nums1.length == m
nums2.length == n
0 <= m <= 1000
0 <= n <= 1000
1 <= m + n <= 2000
-106 <= nums1[i], nums2[i] <= 106

来源：力扣（LeetCode）
链接：https://leetcode.cn/problems/median-of-two-sorted-arrays
著作权归领扣网络所有。商业转载请联系官方授权，非商业转载请注明出处。

题目分析：

参考题解：

class Solution {
public:
    double findMedianSortedArrays(vector<int>& nums1, vector<int>& nums2) 
    {
        //保证nums1的长度小于nums2的长度
        if(nums1.size() > nums2.size())
            return findMedianSortedArrays(nums2, nums1);
        int len = nums1.size() + nums2.size();
        int mid = (len + 1) / 2; //理论中位数的下标 
        int left = 0, right = nums1.size(); //控制nums1
        while(left <= right)
        {
            int i = (left + right) / 2; 
            int j = mid - i;
            double LeftMax = max((i == 0) ? INT_MIN : nums1[i - 1] , (j == 0) ? INT_MIN : nums2[j -  1]); 
            double RightMin = min((i == nums1.size()) ? INT_MAX : nums1[i] , (j == nums2.size()) ? INT_MAX : nums2[j]);  
            if(LeftMax <= RightMin)        
                return len % 2 == 0 ? (LeftMax + RightMin) / 2 : LeftMax;          
            if(((i == 0) ? INT_MIN : nums1[i - 1]) > ((j == 0) ? INT_MIN : nums2[j - 1]))
                right = i - 1;
            else
                left = i + 1;
        }
        return 0;
    }
};