原文链接：http://tecdat.cn/?p=24152
什么是PCR？（PCR = PCA + MLR）（点击文末“阅读原文”获取完整代码数据）。
• PCR是处理许多 x 变量的回归技术
• 给定 Y 和 X 数据：
• 在 X 矩阵上进行 PCA
– 定义新变量：主成分（分数）
• 在 多元线性_回归_(_MLR_) 中使用这些新变量中的一些来建模/预测 Y
• Y 可能是单变量或多变量。
相关视频
例子
# 对数据
set.seed(123)
da1 <- marix(c(x1, x2, x3, x4, y), ncol = 5, row = F)多元线性回归和逐步剔除变量，手动：
# 对于data1：（正确的顺序将根据模拟情况而改变）。
lm(y ~ x1 + x2 + x3 + x4)
lm(y ~ x2 + x3 + x4)
lm(y ~ x2 + x3)
lm(y ~ x3)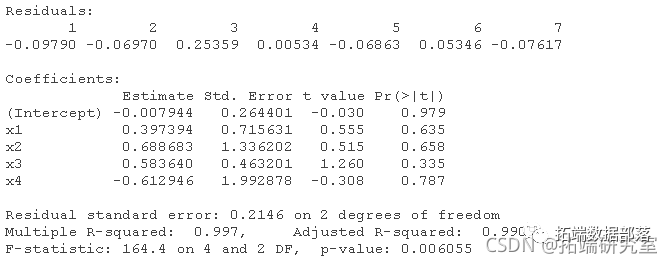
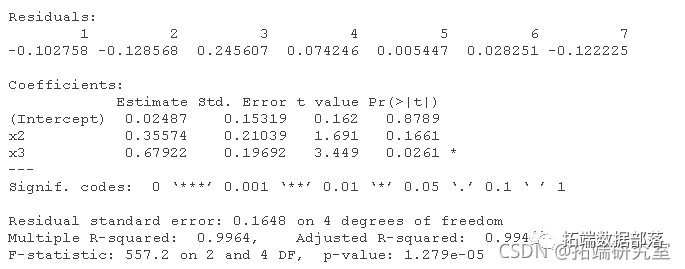
配对关系图
pais(atix, ncol = 5, byrow = F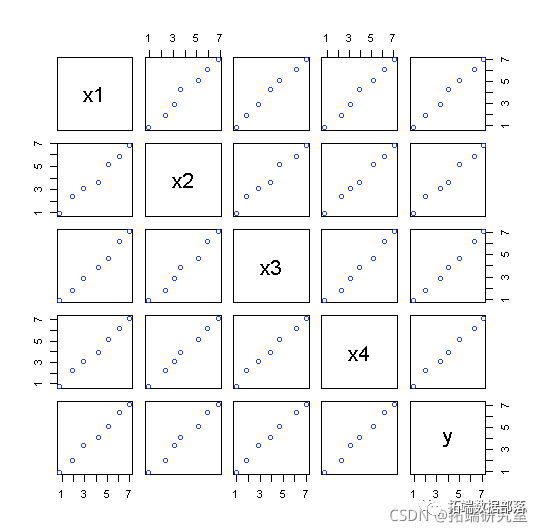
如果对data2重复以上过程：
# 对于data2:
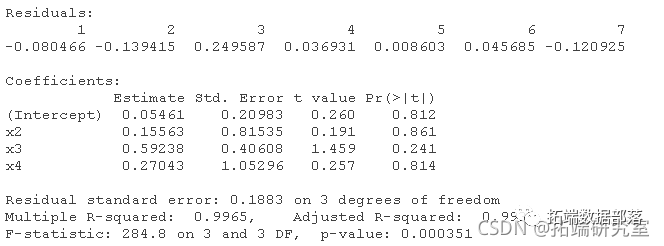
lm(y ~ x1 + x2 + x3 + x4)
lm(y ~ x1 + x2 + x4)
lm(y ~ x2 + x4)
lm(y ~ x2)
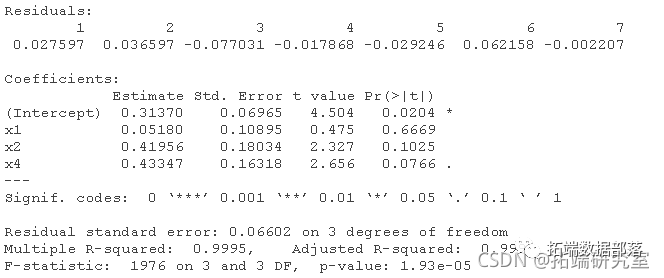
数据集 2 的绘图：
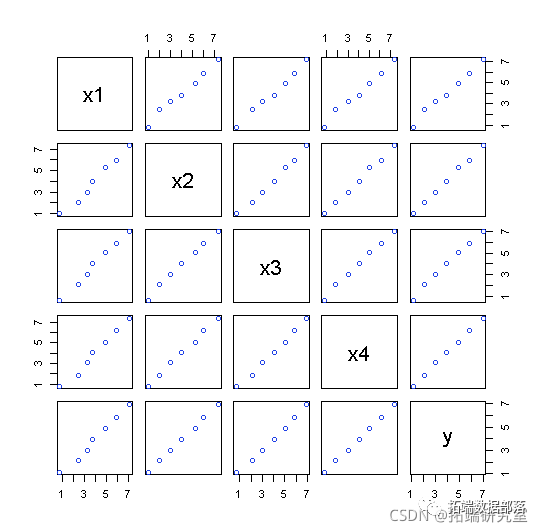
使用四个 x 的均值作为单个变量来分析两个数据集：
xn1 <- (dt1\[,1\] + a1\[,2\] + at1\[,3\] + dt1\[,4\])/4
lm(data1\[,5\] ~ xn1)
lm(data2\[,5\] ~ xn2)
检查一下X数据的PCA的载荷loading是什么。
# 几乎所有的方差都在第一主成分解释。
prnmp(dt1\[,1:4\])
# 第一个成分的载荷
picp(dta1\[,1:4\])$lads\[,1\]
它们几乎相同，以至于第一个主成分本质上是四个变量的平均值。让我们保存一些预测的 beta 系数 - 一组来自数据 1 的完整集和一组来自均值分析的：
c1 <- smry(lm(dta1\[,5\] ~ dta1\[,1\] + dta1\[,2\] + ata1\[,3\] +
dt1\[,4\]))$coficns\[,1\]
f <- summry(rm2)$cefets\[,1\]我们现在模拟三种方法（完整模型、均值（=PCR）和单个变量）在 7000 次预测中的表现：
# 对预测进行模拟。
误差<- 0.2
xn <- (x1 + x2 + x3 + x4)/4
yt2 <- cf\[1\] + cf\[2\] * xn
yht3 <- cf\[1\] + cf\[2\] * x3
bro(c(um((y-hat)^2)/7000 min = "平均预测误差平方")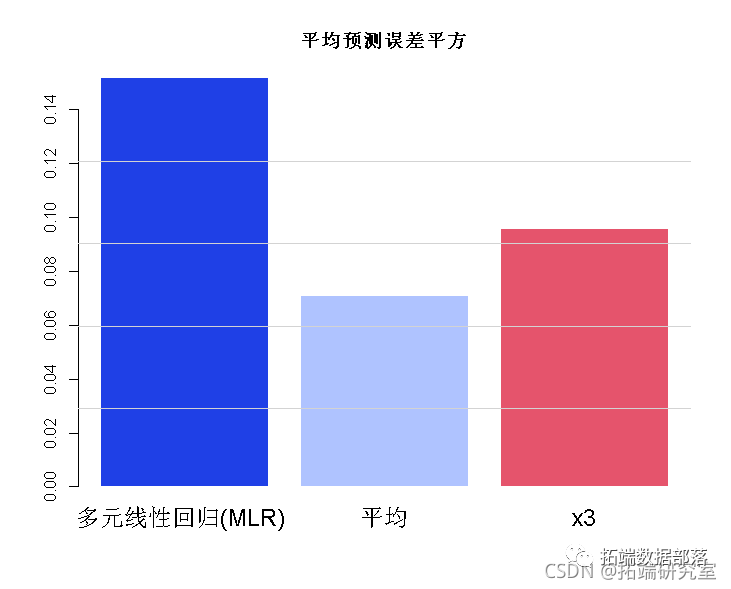
PCR 分析误差最小。
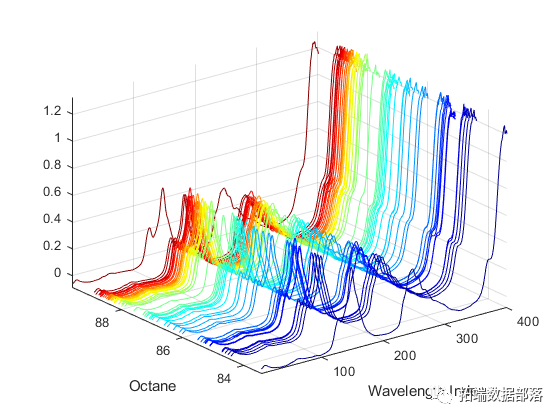
示例：光谱类型数据
构建一些人工光谱数据：（7 个观测值，100 个波长）
# 光谱数据实例
mapot(t(spcra) )
mtlnes(t(spcra))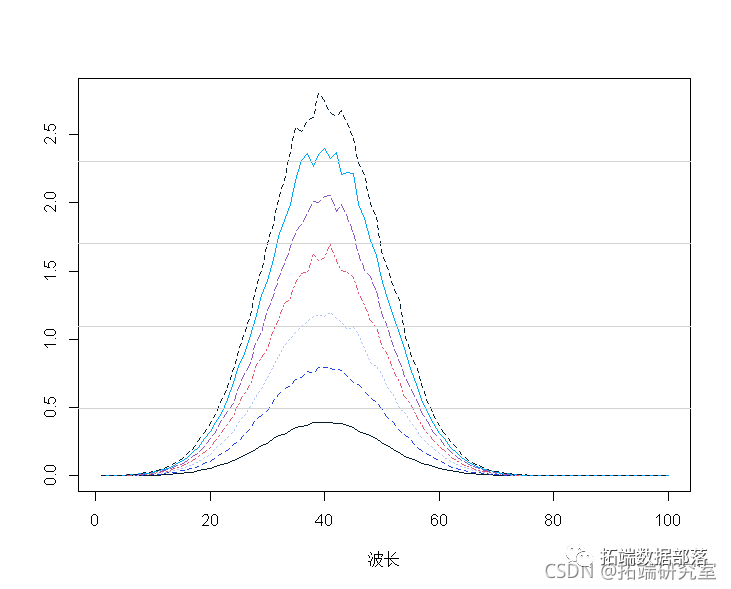
平均光谱表明：
mtpot(t(secra))
malies(t(spcta))
mnp <- apply(spcra, 2, mean)
lines(1:100, mnp, lwd = 2)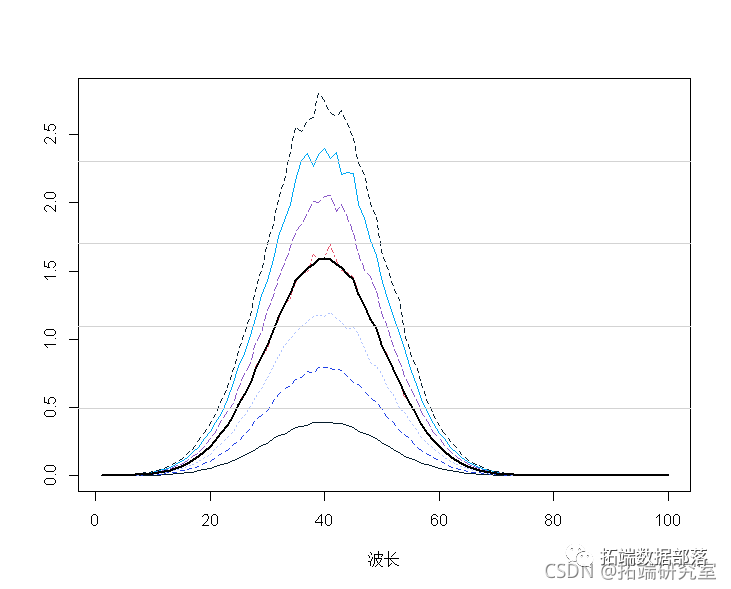
平均中心光谱：
spcamc<-scae(spcta,scale=F)
plot(t(spermc),tpe="")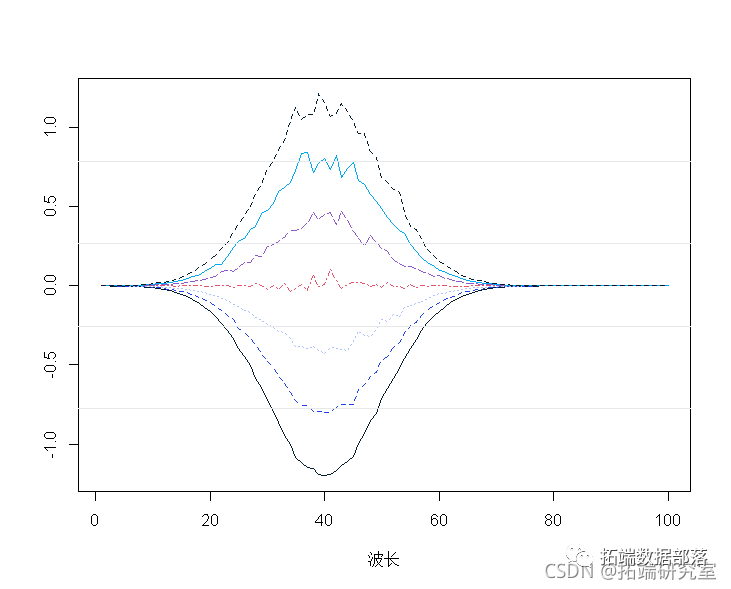
点击标题查阅往期内容
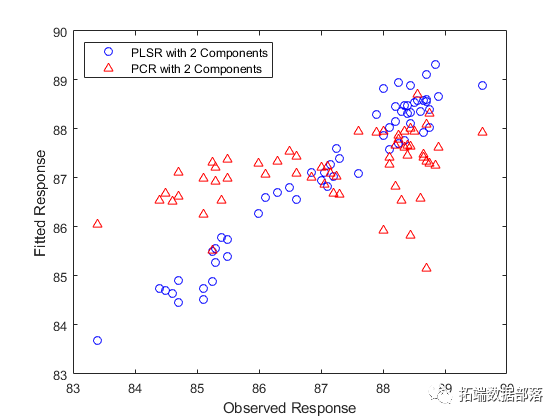
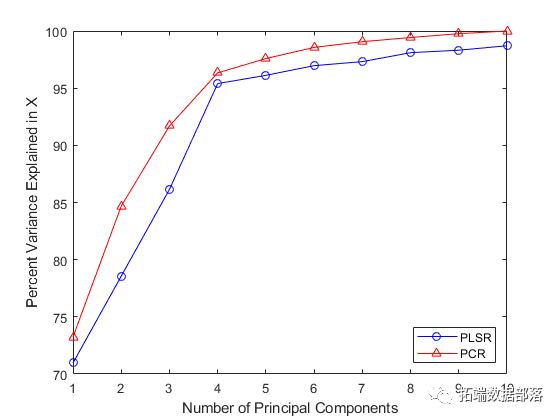
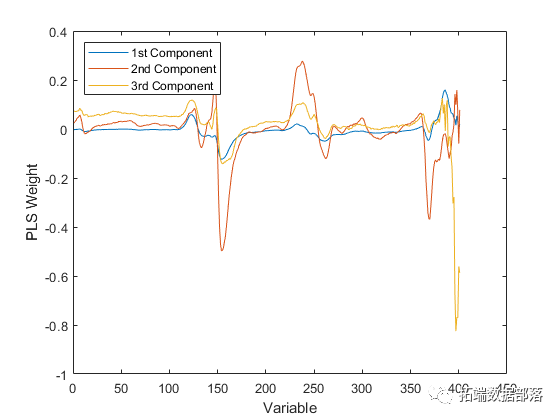
偏最小二乘回归（PLSR）和主成分回归（PCR）
左右滑动查看更多
01
02
03
04
标准化光谱：
sptracs<-scale(spetra,scale=T,center=T)
matott(specrams),tye="n",
matlies(t(sectramcs))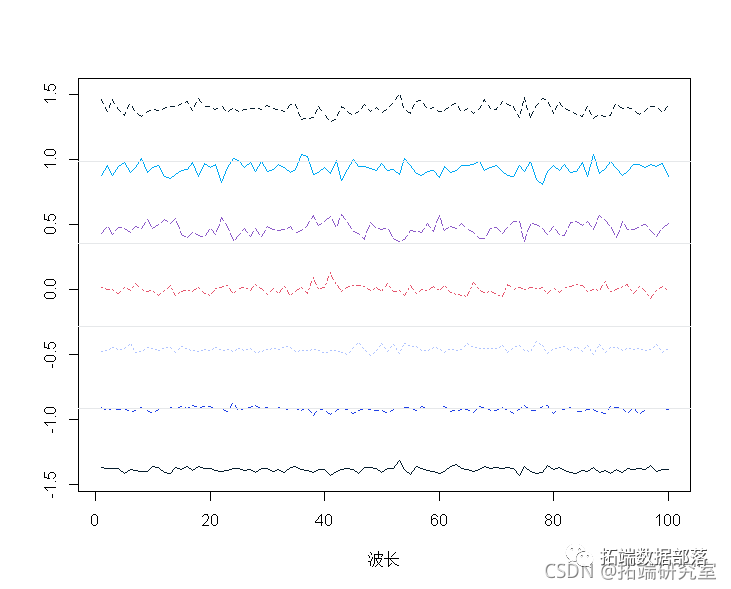
# 用特征函数对相关矩阵做PCA。
pcaes <- eien(cor(spra))
ladigs <- pces$vectors\[,1\].
score <- peramcs%*%t(t(lodis1))
pred <- soes1 %*% loadings1
## 1-PCA预测值转换为原始尺度和平均值。
mtrx(repeasp, 7), nro=7, brw=T)在单个概览图中收集的所有图：
par(mfrow = c(3, 3)
matlot(t(sectr)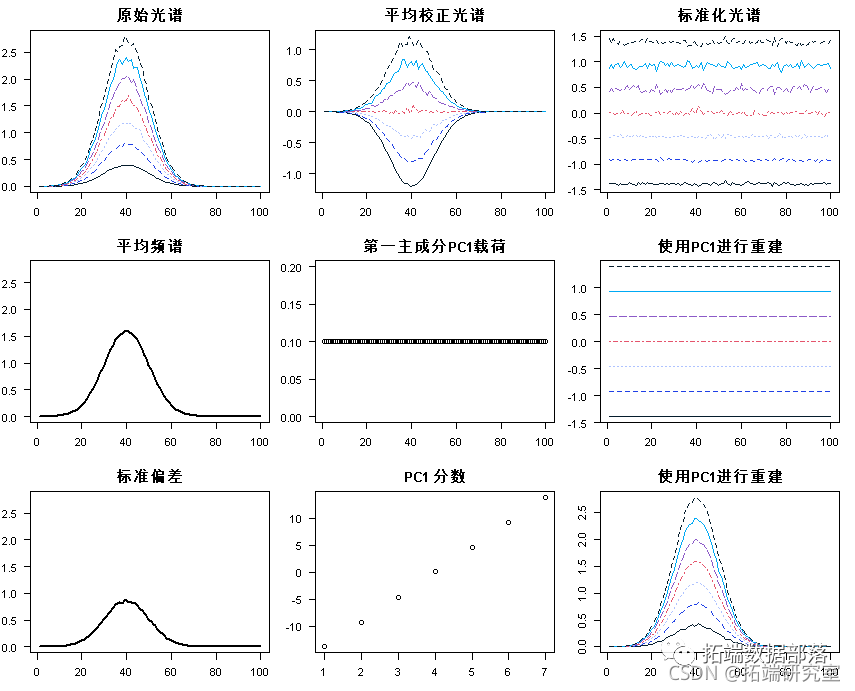
PCR是什么？
• 数据情况：
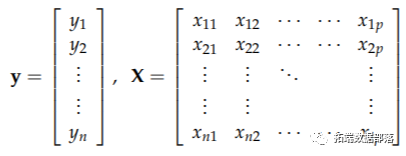
• 用A 主成分t1、t2... 做MLR而不是所有（或部分）x。
• 多少个成分：通过交叉验证确定。
怎么做？
1. 探索数据
2. 进行建模（选择主成分数量，考虑变量选择）
3. 验证（残差、异常值、影响等）
4. 迭代 2. 和 3。
5. 解释、总结、报告。
6. 如果相关：预测未来值。
交叉验证
• 忽略一部分观察值
• 在剩余（减少的）数据上拟合模型
• 预测模型遗漏的观察值：yˆi,val
• 对所有观察值依次执行此操作并计算总体模型性能：
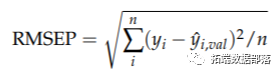（预测的均方根误差）
最后：对所有选择的分量（0、1、2、...、... ）进行交叉验证并绘制模型性能
barplot(names.arg)
选择最佳成分数：
• 总体误差最小的主成分。
重采样
• 交叉验证 (CV)
•留一法(_Leave-On_e-_Out_,简称LOO)
• Bootstrapping
• 一个很好的通用方法：
– 将数据分成训练集和测试集。
– 在训练数据上使用交叉验证
– 检查测试集上的模型性能
– 可能：重复所有这些多次（重复双交叉验证）
交叉验证 - 原则
• 最小化预期预测误差：
平方预测误差 = Bias2 +方差
• 包括“许多”PC主成分：低偏差，但高方差
• 包括“很少”PC 主成分：高偏差，但低方差
• 选择最佳折衷！
验证 - 存在于不同的级别
1. 分为 3 个：训练（50%）、验证（25%）和测试（25%）
2. 拆分为 2：校准/训练 (67%) 和测试 (33%)
训练中，CV/bootstrap •更常用
3. 没有 "固定分割"，而是通过CV/bootstrap反复分割，然后在每个训练组内进行CV。
4. 没有分割，但使用（一级）CV/bootstrap。
5. 只对所有数据进行拟合--并检查误差。
示例：汽车数据
# 例子：使用汽车数据。
# 将X矩阵定义为数据框中的一个矩阵。
mtas$X <- as.ix(mcas\[, 2:11\])
# 首先，我们考虑随机选择4个属性作为测试集
mtcrs_EST<- mtcrs\[tcars$rai == FASE,\] 。
tcaTRAIN <- mtars\[tcarstrai == TUE,\] 。现在所有的工作都在 训练数据集上进行。
探索数据
我们之前已经这样做了，所以这里不再赘述
数据建模
使用pls软件包以最大/大量的主成分运行PCR。
# 使用pls软件包，以最大/较大的成分数运行PCR。
pls(lomg ~ X , ncop = 10, dta = marsTRAN,
aliaon="LOO")初始图集：
# 初始化的绘图集。
par(mfrow = c(2, 2)
plot(mod)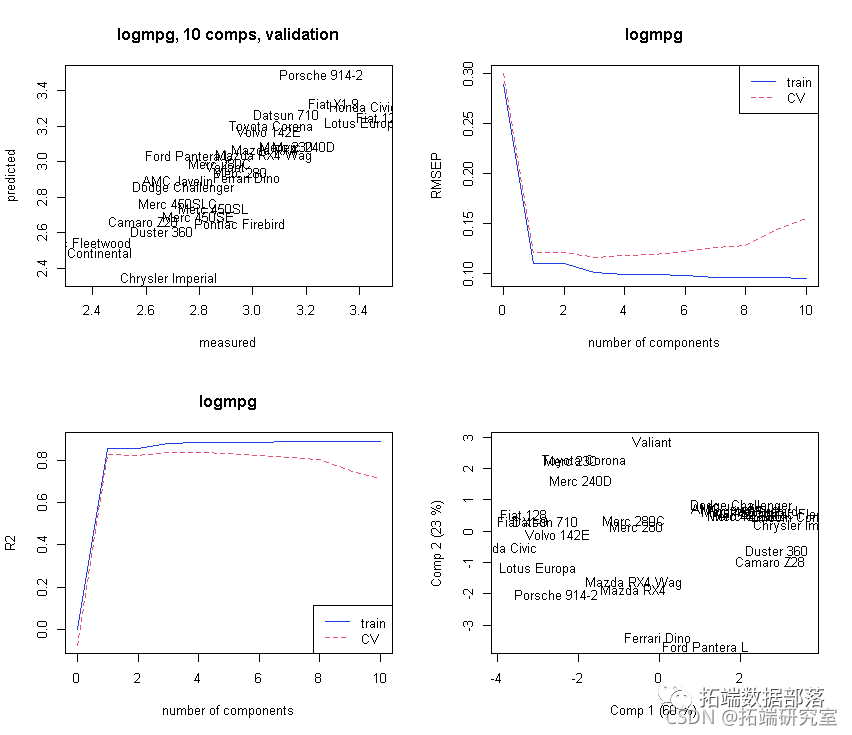
主成分的选择：
# 主成分的选择。
# 分段的CV会得到什么。
modseCV <- pcr(lomg ~ X , ncp = 10, dta = marTIN
vai ="CV"
)
# 初始图集。
par(mfrow = c(1, 2))
plot(odsC, "vadaion")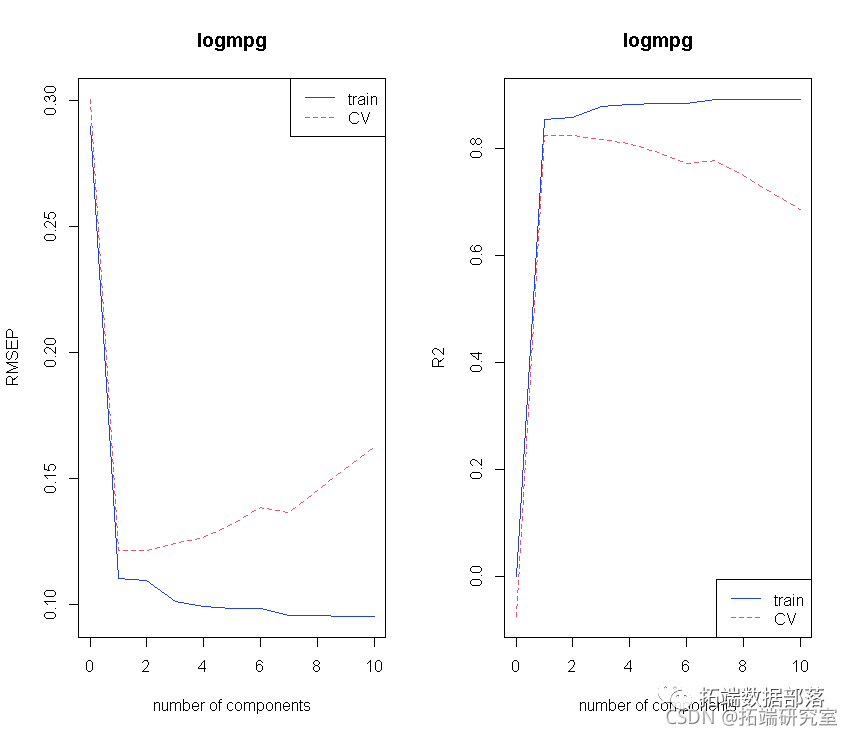
让我们看看更多的主成分：
# 让我们看看更多的主成分。
# 分数。
scre(mod)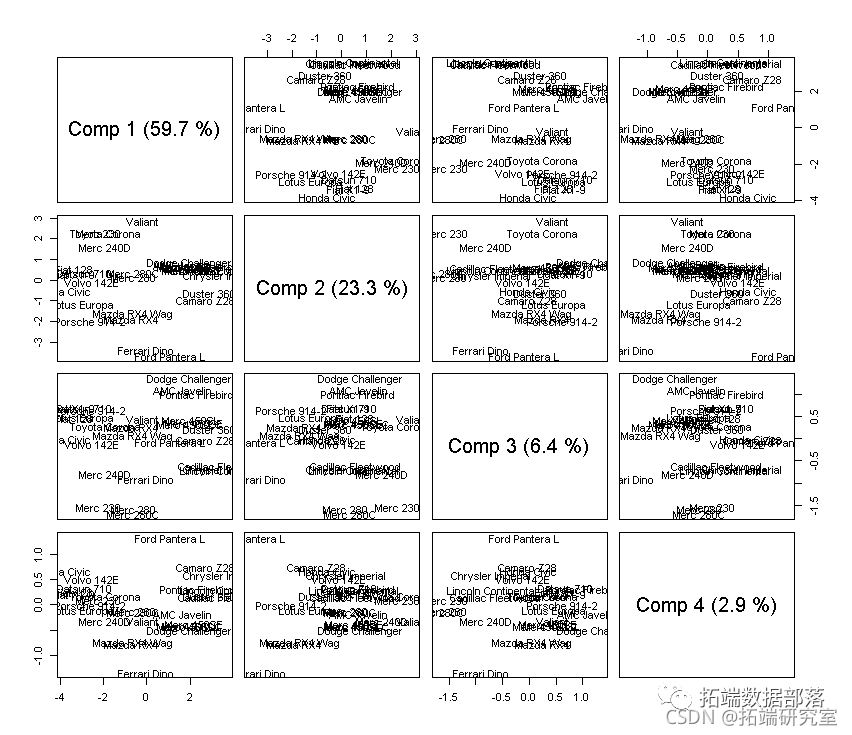
#负荷
loading(md,cms = 1:4)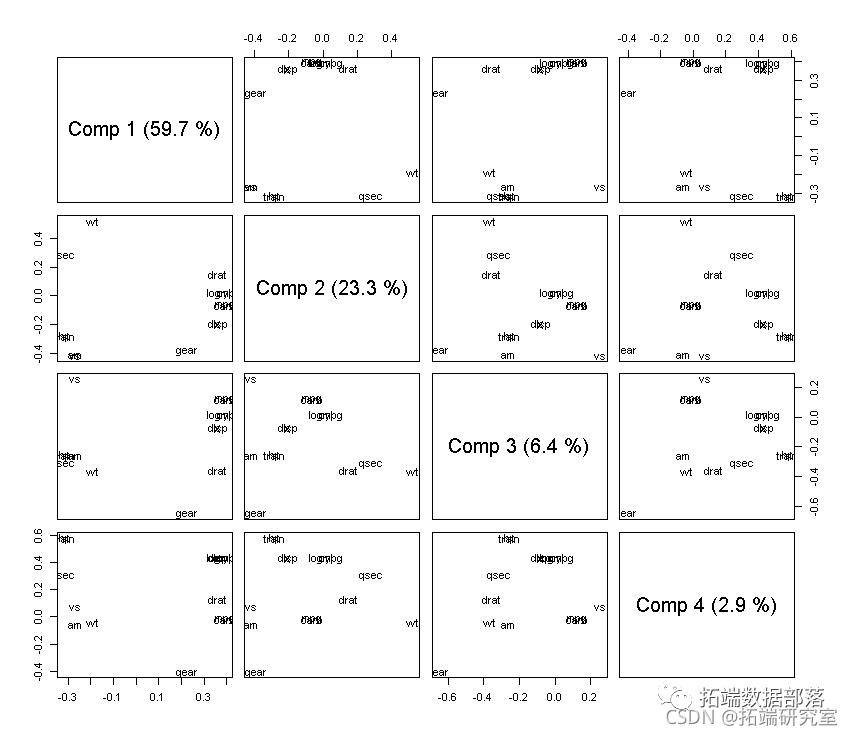
我们选择 3 个主成分：
# 我们选择4个成分
m <- ncmp = 3, data = mrs_TAI vdon = "LOO", akknie = RUE然后：验证：
让我们验证更多：使用 3 个主成分。我们从中获取预测的残差，因此这些是（CV）验证版本！
oit <- ppo(mod3, whih = "litin")
plot(obft\[,2\], Rsds)
# 为了绘制残差与X-杠杆的对比，我们需要找到X-杠杆。
# 然后找到杠杆值作为Hat矩阵的对角线。
# 基于拟合的X值。
Xf <- sors(md3)
plot(lvge, abs(Rsidals))
text(leage, abs(Reuls))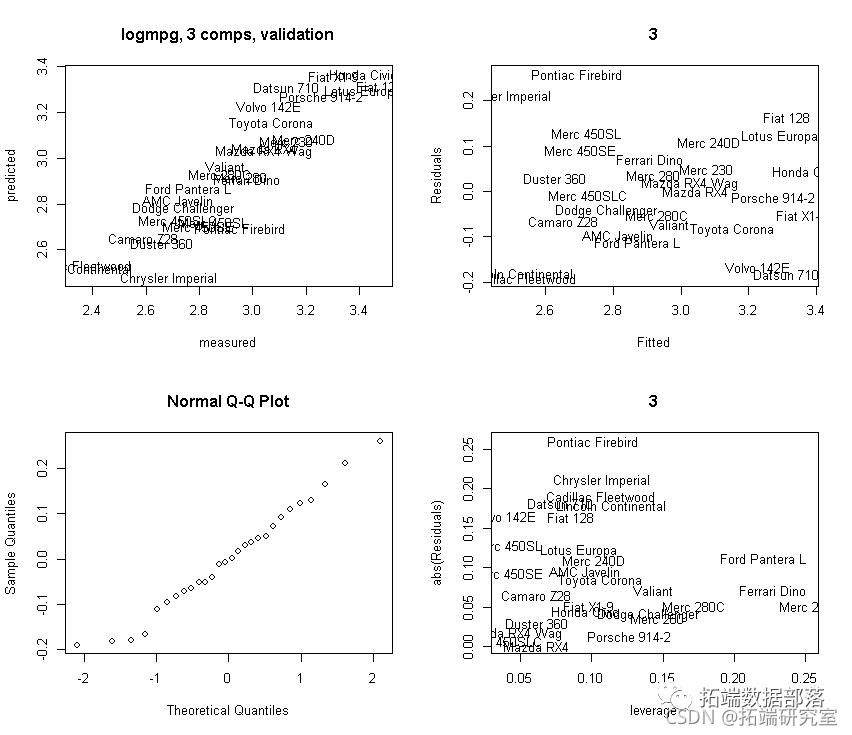
# 让我们也绘制一下残差与每个输入X的关系。
for ( i in 2:11){
plot(res~masAN\[,i\],type="n")
}
解释/结论
现在让我们看一下结果——“解释/结论”：
# 现在我们来看看结果 - 4) "解释/结论"
par(mfrw = c(2, 2))
# 绘制具有Jacknife不确定性的系数。
obfi <- red(mod3,, wich = "vltn)
abe(lm(ft\[,2\] ~ fit\[,1\])
plt(mo3, ses = TUE,)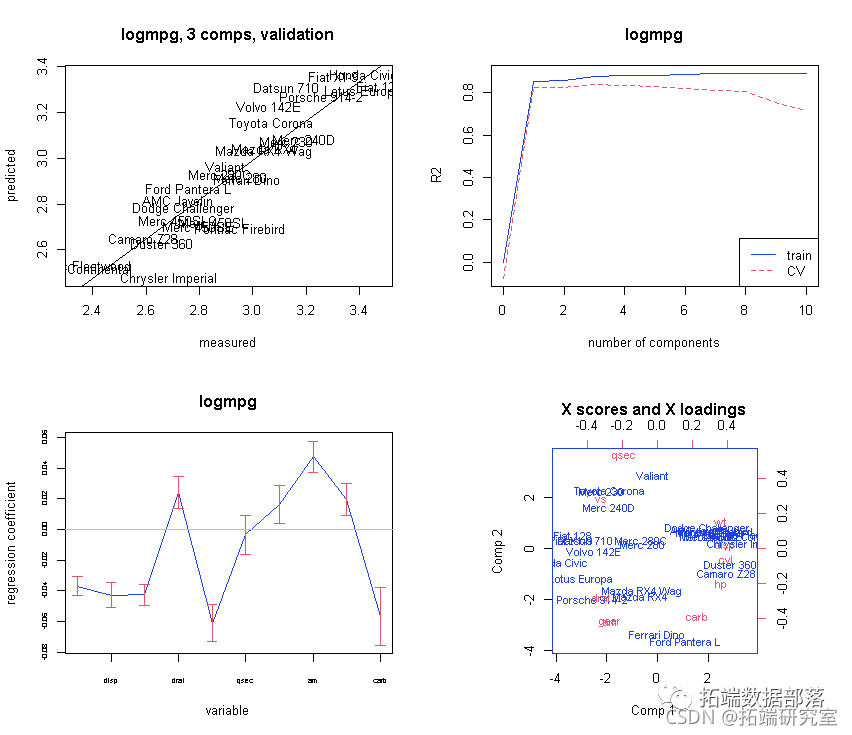
# 最后是一些输出
test(mo3, nm = 3)
预测
# 现在让我们试着预测TEST集的4个数据点。
prdit(md3, nwaa =TEST)
plt(TEST$lgg, pes)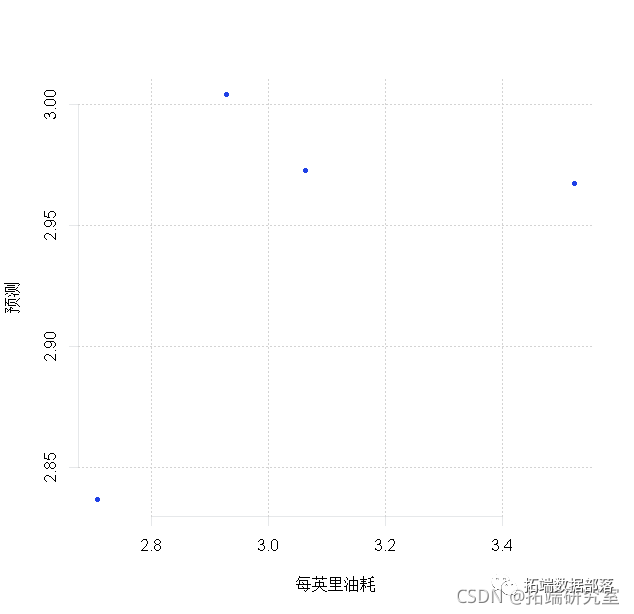
rmsep <- sqrt(men(log - prd)^2))
rmsep
点击文末“阅读原文”
获取全文完整代码数据资料。
本文选自《R语言主成分回归（PCR）、 多元线性回归特征降维分析光谱数据和汽车油耗、性能数据》。
点击标题查阅往期内容
R语言主成分PCA、因子分析、聚类对地区经济研究分析重庆市经济指标
数据分享|R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化
R语言逻辑回归logistic模型分析泰坦尼克titanic数据集预测生还情况
R语言是否对二分连续变量执行逻辑回归
R语言用lme4多层次（混合效应）广义线性模型（GLM），逻辑回归分析教育留级调查数据
R语言随机森林RandomForest、逻辑回归Logisitc预测心脏病数据和可视化分析
R语言基于Bagging分类的逻辑回归(Logistic Regression)、决策树、森林分析心脏病患者
R语言逻辑回归（Logistic回归）模型分类预测病人冠心病风险
R语言用局部加权回归(Lowess)对logistic逻辑回归诊断和残差分析
R语言用主成分PCA、 逻辑回归、决策树、随机森林分析心脏病数据并高维可视化
R语言用线性模型进行臭氧预测：加权泊松回归，普通最小二乘，加权负二项式模型，多重插补缺失值
R语言Bootstrap的岭回归和自适应LASSO回归可视化
R语言中回归和分类模型选择的性能指标
R语言多元时间序列滚动预测：ARIMA、回归、ARIMAX模型分析
R语言用lme4多层次（混合效应）广义线性模型（GLM），逻辑回归分析教育留级调查数据
R语言计量经济学：虚拟变量(哑变量)在线性回归模型中的应用
R语言 线性混合效应模型实战案例
R语言混合效应逻辑回归（mixed effects logistic）模型分析肺癌数据
R语言如何用潜类别混合效应模型（LCMM）分析抑郁症状
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言建立和可视化混合效应模型mixed effect model
R语言LME4混合效应模型研究教师的受欢迎程度
R语言 线性混合效应模型实战案例
R语言用Rshiny探索lme4广义线性混合模型（GLMM）和线性混合模型（LMM）
R语言基于copula的贝叶斯分层混合模型的诊断准确性研究
R语言如何解决线性混合模型中畸形拟合(Singular fit)的问题
基于R语言的lmer混合线性回归模型
R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型
R语言分层线性模型案例
R语言用WinBUGS 软件对学术能力测验（SAT）建立分层模型
使用SAS，Stata，HLM，R，SPSS和Mplus的分层线性模型HLM
R语言用WinBUGS 软件对学术能力测验建立层次（分层）贝叶斯模型
SPSS中的多层（等级）线性模型Multilevel linear models研究整容手术数据
用SPSS估计HLM多层（层次）线性模型模型
R语言高维数据的主成分pca、 t-SNE算法降维与可视化分析案例报告
R语言惩罚logistic逻辑回归（LASSO,岭回归）高维变量选择的分类模型案例
R语言有RStan的多维验证性因子分析（CFA）
主成分分析(PCA)原理及R语言实现及分析实例
R语言无监督学习：PCA主成分分析可视化
R语言使用Metropolis- Hasting抽样算法进行逻辑回归
R语言多元Logistic逻辑回归 应用案例
R语言自适应LASSO 多项式回归、二元逻辑回归和岭回归应用分析
R语言用逻辑回归、决策树和随机森林对信贷数据集进行分类预测
R语言基于树的方法：决策树，随机森林，Bagging，增强树
spss modeler用决策树神经网络预测ST的股票
R语言中自编基尼系数的CART回归决策树的实现
python在Scikit-learn中用决策树和随机森林预测NBA获胜者
matlab使用分位数随机森林（QRF）回归树检测异常值
基于随机森林、svm、CNN机器学习的风控欺诈识别模型
R语言惩罚logistic逻辑回归（LASSO,岭回归）高维变量选择的分类模型案例
R语言用标准最小二乘OLS，广义相加模型GAM ，样条函数进行逻辑回归LOGISTIC分
