1. 题目介绍（68. 二叉树中两个节点的最低公共祖先）

面试题68：二叉树中两个节点的最低公共祖先，一共分为两小题：

题目一：二叉搜索树的最近公共祖先
题目二：二叉树的最近公共祖先

2. 题目1：二叉搜索树的最近公共祖先

题目链接：https://leetcode.cn/problems/er-cha-sou-suo-shu-de-zui-jin-gong-gong-zu-xian-lcof/

2.1 题目介绍

给定一个二叉搜索树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

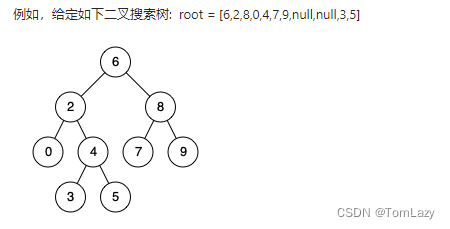
在这里插入图片描述

【测试用例】：
在这里插入图片描述
【条件约束】：

【相关题目】：

注意：本题与主站 235. 二叉搜索树的最近公共祖先题目相同。

2.2 题解 – 迭代/递归 O(n) ⭐

时间复杂度O(n)，空间复杂度O(n)
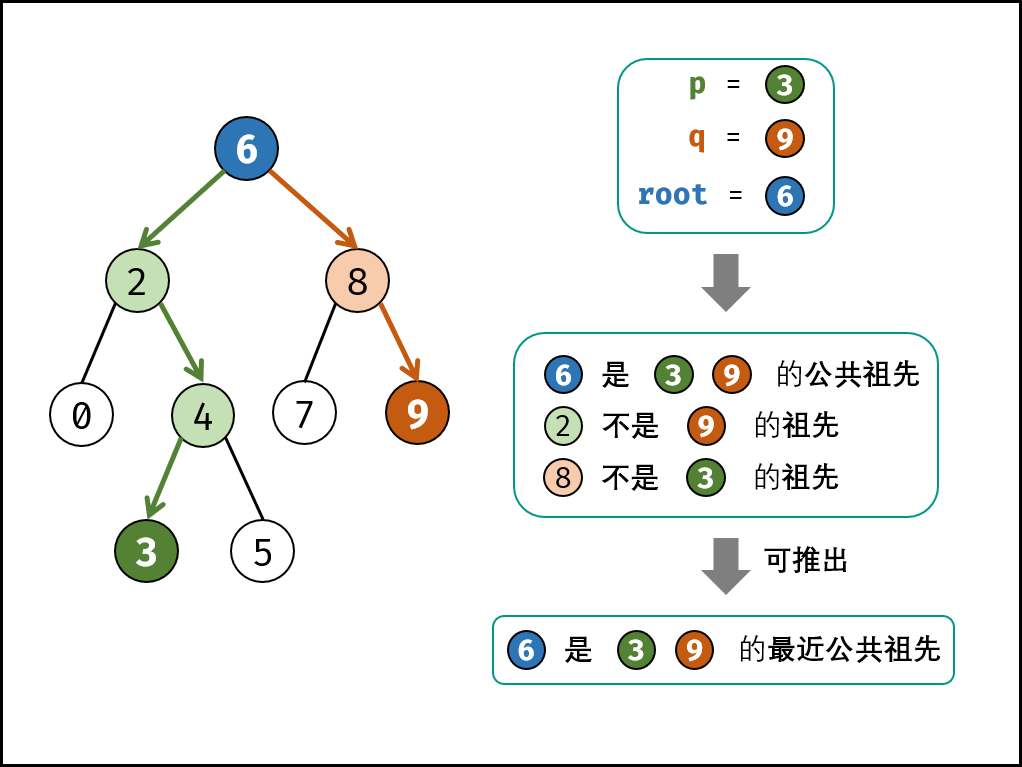
在这里插入图片描述

【解题思路】：
由于二叉搜索树的性质，我们很容易就能找出两个节点的最低公共祖先。
……
二叉搜索树：位于左子树的节点的都小于父节点，位于右子树的节点都大于父节点；
因此，根据二叉搜索树的特性，我们只需要从树的根节点开始和两个输入的节点进行比较：

如果当前节点的值比两个节点的值都大，那么最低的共同父节点一定在当前节点的左子树上；
如果当前节点的值比两个节点的值都小，那么最低的共同父节点一定在当前节点的右子树上；
如果一大一小，那么当前节点即为其最低的共同父节点。

……
【实现策略】：
根据以上思路，实现方法可分为两种：

迭代法
递归法

迭代法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        while (root != null) {
            if (root.val > p.val && root.val > q.val) root = root.left;
            else if (root.val < p.val && root.val < q.val) root = root.right;
            else break;
        }
        return root;
    }
}

在这里插入图片描述
递归法：

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if(root.val < p.val && root.val < q.val)
            return lowestCommonAncestor(root.right, p, q);
        if(root.val > p.val && root.val > q.val)
            return lowestCommonAncestor(root.left, p, q);
        return root;
    }
}

在这里插入图片描述

3. 题目2：二叉树的最近公共祖先

题目链接：https://leetcode.cn/problems/er-cha-shu-de-zui-jin-gong-gong-zu-xian-lcof/

3.1 题目介绍

给定一个二叉树, 找到该树中两个指定节点的最近公共祖先。

百度百科中最近公共祖先的定义为：“对于有根树 T 的两个结点 p、q，最近公共祖先表示为一个结点 x，满足 x 是 p、q 的祖先且 x 的深度尽可能大（一个节点也可以是它自己的祖先）。”

在这里插入图片描述

【测试用例】：

【条件约束】：

【相关题目】：

注意：本题与主站 236. 二叉树的最近公共祖先题目相同.

3.2 题解 – 递归 O(n) ⭐

时间复杂度O(n)，空间复杂度O(n)

【解题思路】：
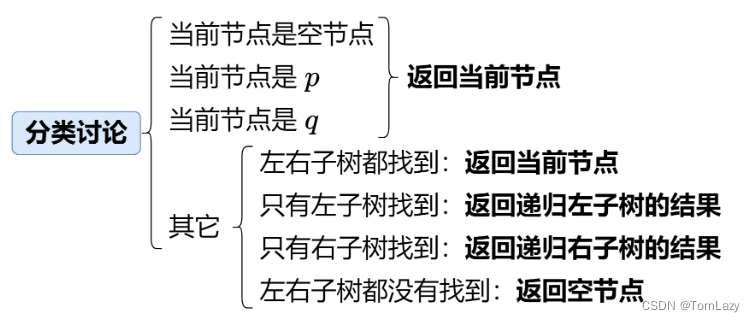
对于二叉树来说，与二叉搜索树不同之处就在于，没有了排序，无法直接根据值的大小来判断 p、q 存在的位置，那么我们要想找到二叉树中两个节点的最低公共祖先，就需要遍历一遍二叉树，对此我们可以进行分类讨论：

……
【实现策略】：

首先判断当前节点是否为空，是否为 p 和 q 将其作为递归的结束条件；

分类讨论：

当左右子树都找到时，返回当前节点；
当只有左子树找到时，返回递归左子树的结果；
当只有右子树找到时，返回递归右子树的结果；
当左右子树都没找到时，返回空节点（此步可合并到2、3步省略）

大家是否存在这样一个疑惑，就是假设只有左子树找到，右子树没找到，那么返回左子树结果是否正确，验证后结果确实正确，这是因为，如果出现这种情况就说明输入的两个节点，其中有一个节点不是这个二叉树上的值，与题目中的说明不符，题目中说明的是两个节点都存在与二叉树中，不过出现这种情况返回的依旧是存在的那个输入节点，判定结果仍是对的。

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    // 递归，分类讨论
    // 左右都有，返回当前节点
    // 左边有，返回左边
    // 右边有， 返回右边
    // 左右都没有，返回null
    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q) return root;
        TreeNode left = lowestCommonAncestor(root.left,p,q);  // 左子树递归
        TreeNode right = lowestCommonAncestor(root.right,p,q);  // 右子树递归
        if (left != null && right != null) return root;
        return left != null ? left : right;     
    }
}