树在我们底层结构中是被广泛运用的,但是为什么会选择它却是我们需要了解的东西,接下来 让我们一起走进树的世界
请看下图:

在我们生活中,有很多关于树的存在,比如电脑中的磁盘(C D盘),在文章中写的目录都是树的一种的体现,接下来让你们深入了解树这种的数据结构
二分查找树
特点
1.动态数据结构(不需要动态扩容)
2.具有唯一的根结点
3.天然的递归结构
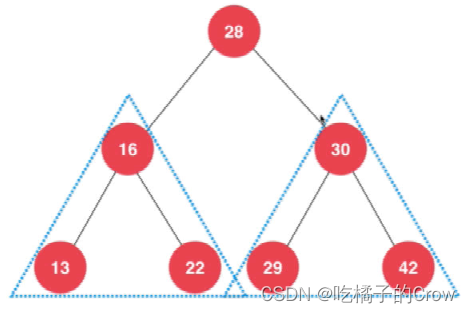
满二叉树
定义:除最后一层无任何子节点外,每一层上的所有结点都有两个子结点的二叉树

以上树均不为满二叉树
假设有一个K层深的树
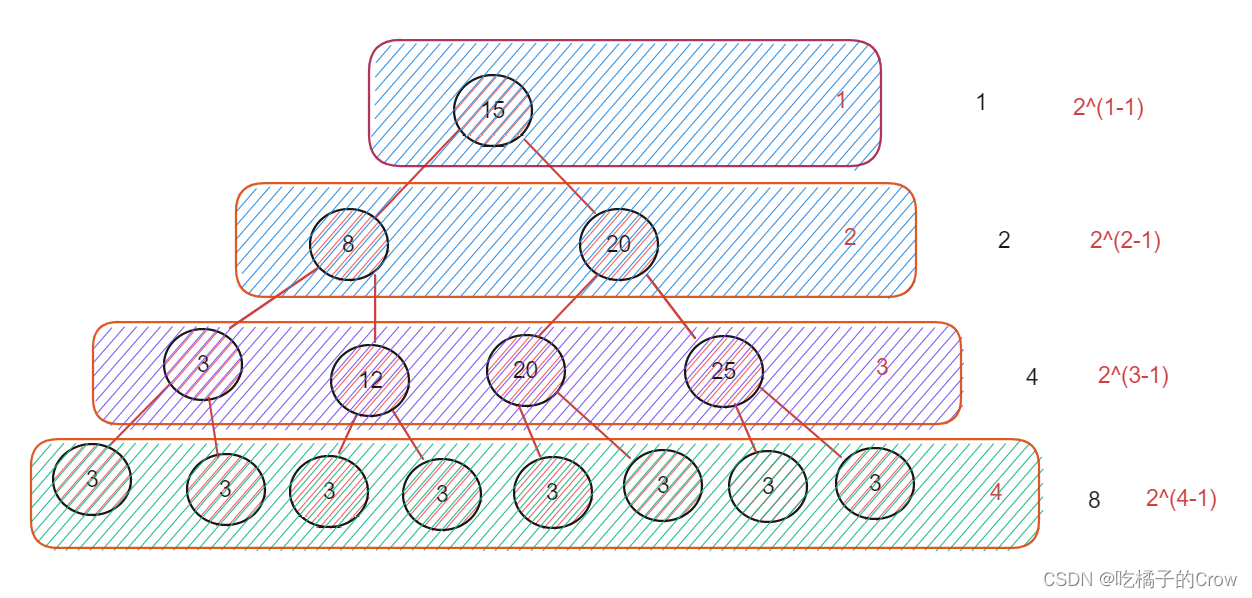
叶子节点数:2^(k-1)

总叶子结点数:2^k-1

非叶子结点数:2^(k-1)-1

树的空间复杂度:O(logn)
下面是树方法的最基本的是实现:
//对节点进行初始化
class Node{
T ele;
Node left;
Node right;
public Node(T ele){
this.ele=ele;
this.left=null;
this.right=null;
}
}
//对搜索二叉树进行初始化
private Node root;
private int size;
public BinarySearchTree(){
this.root=null;
this.size=0;
}
//对外提供增加方法
public void add(T ele){
this.root=add(this.root,ele);
}
//实际调用的增加的方法
private Node add(Node node,T ele){
//如果node为空的话,直接在根节点进行添加
if(node==null){
Node addNode=new Node(ele);
this.size++;
return addNode;
}
//若添加的节点与对应的根节点进行比较,小于的话直接挂接在左子树上
if(ele.compareTo(node.ele)<0){
node.left=add(node.left,ele);
//大于等于挂接在右子数上
}else{
node.right=add(node.right,ele);
}
return node;
}
//对外提供的查询方法
public Boolean search(T ele){
return search(this.root,ele);
}
//实际调用的方法
private Boolean search(Node node,T ele){
if(node==null){
return false;
}
if(ele.compareTo(node.ele)>0){
return search(node.right,ele);
}else if(ele.compareTo(node.ele)<0){
return search(node.left,ele);
}else{
return true;
}
}
//中序遍历(DFS)
public void mtraversal(){
middleTraversal(this.root);
}
private void middleTraversal(Node node){
if(node==null){
return;
}
middleTraversal(node.left);
System.out.println(node.ele);
middleTraversal(node.right);
}
//前序遍历(DFS)
public void btraversal(){
beforeTraversal(this.root);
}
private void beforeTraversal(Node node){
if(node==null){
return;
}
System.out.println(node.ele);
beforeTraversal(node.left);
beforeTraversal(node.right);
}
//后续遍历(DFS)
public void atraversal(){
afterTraversal(this.root);
}
private void afterTraversal(Node node){
if(node==null){
return;
}
afterTraversal(node.left);
afterTraversal(node.right);
System.out.println(node.ele);
}
//层序遍历(BFS)使用队列进行保存
public void ltraversal(){
String sb= levelTraversal(this.root);
System.out.println(sb);
}
//实际调用的层序遍历方法
private String levelTraversal(Node node){
//如果头结点为空,直接返回
if(node==null){
return null;
}
//创建一个队列
Queue<Node> queue=new LinkedList<Node>();
queue.offer(node);
StringBuilder sb=new StringBuilder();
//如果该节点不为空,进行遍历,输出
while(!queue.isEmpty()){
Node curNode=queue.poll();
sb.append(curNode.ele+",");
//如果左子树不为空的话,入队
if(curNode.left!=null){
queue.offer(curNode.left);
}
//如果右子树不为空的话入队
if(curNode.right!=null){
queue.offer(curNode.right);
}
}
return sb.toString().substring(0,sb.length()-1) ;
}
//在二分搜索树中找到最大值(使用递归方法)
public Optional<T> getmax(){
if (this.root == null) {
return Optional.empty();
}
Node node=getMax(this.root);
return Optional.of(node.ele);
}
private Node getMax(Node node){
//递归的终止条件
if(node.right==null){
return node;
}
//当节点不为空的时候,进行递归
return getMax(node.right);
}
//在二分搜索树中找到最大值
public Optional<T> getMax1(){
if (this.root == null) {
return Optional.of(null);
}
Node curNode=this.root;
while(curNode.right!=null){
curNode=curNode.right;
}
return Optional.of(curNode.ele);
}
//在二分搜索树中找到最小值(递归)
public Optional<T> getmin(){
if (this.root == null) {
return Optional.empty();
}
Node node=getMin(this.root);
return Optional.of(node.ele);
}
private Node getMin(Node node){
//递归的终止条件
if(node.left==null){
return node;
}
//当节点不为空的时候,进行递归
return getMin(node.left);
}
//在二分搜索树中找到最小值
public Optional<T> getMin2(){
if(this.root==null){
return Optional.of(null);
}
Node curNode=this.root;
while(curNode.left!=null){
curNode=curNode.left;
}
return Optional.of(curNode.ele);
}
//删除树中的最大结点
public T removeMaxNode(){
//查找最大的结点
Optional<T> optional=getmax();
//判断是否存在
if(!optional.isPresent()){
return null;
}
//分析存在的情况
this.root=removeMaxNode(this.root);
return optional.get();
}
// 从以node为根的二分搜索树中删除最大的结点
private Node removeMaxNode(Node node) {
// 递归到底的情况
if (node.right == null) {
this.size--;
// 进行删除
return node.left;
}
// 递归操作
node.right = removeMaxNode(node.right);
return node;
}
//删除任意结点
public boolean remove(T ele){
//判断值为ele的结点在树中是否存在
boolean result=search(ele);
if(result){
//使用递归的方式进行是删除
this.root=remove(this.root,ele);
}
return result;
}
//以node为根的二分搜索树中删除结点值为ele的结点
private Node remove(Node node,T ele){
//递归终止条件
if(node.ele.compareTo(ele)==0){
this.size--;
if(node.left==null){
return node.right;
}else if(node.right==null){
return node.left;
}else{
//先从删除结点的左子树中找到最大
Node preNode=getMax(node.left);
//从左子树删除最大的元素
Node rightNodeRoot=removeMaxNode(node.left);
//进行挂接
preNode.right=node.right;
preNode.left=rightNodeRoot;
this.size++;
return preNode;
}
}
if(ele.compareTo(node.ele)>0){
node.right=remove(node.right,ele);
}else{
node.left=remove(node.left,ele);
}
return node;
}
@Override
public String toString() {
return "当前节点的个数为:"+this.size;
}