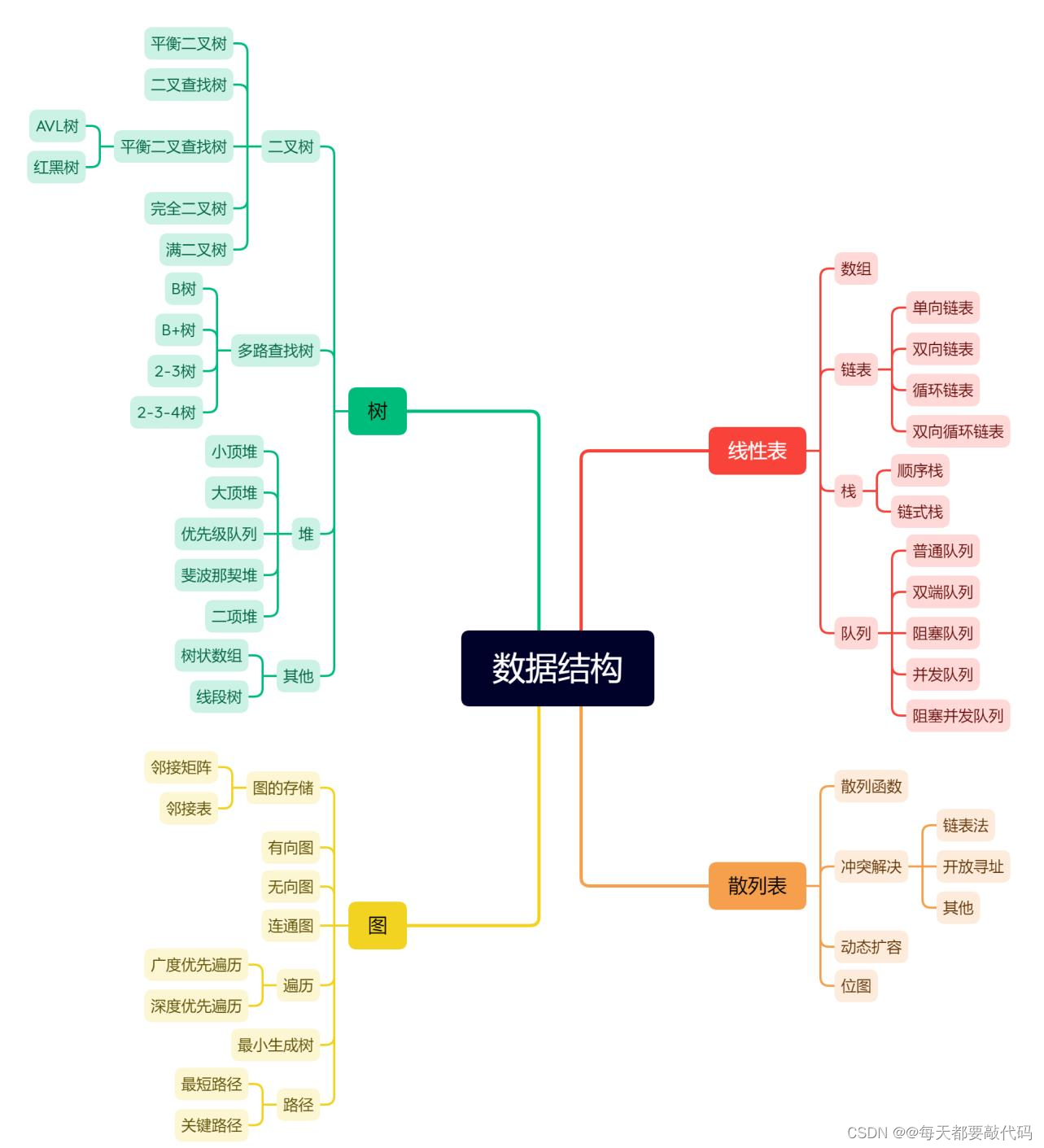
目录
一:数据结构
1. 数据结构剖析
1.1 研究对象一:数据间逻辑关系
1.2 研究对象二:数据的存储结构(或物理结构)
1.3 研究对象三:运算结构
2. 常见存储结构之:数组
3. 常见存储结构之:链表
4. 常见存储结构之:栈
5. 常见存储结构之:队列
6. 常见存储结构之:树与二叉树
6.1 树的理解
6.2 二叉树的基本概念
6.3 二叉树的遍历
6.4 经典二叉树
二:常用集合的源码分析
1. List 接口分析
1.1 List接口特点
1.2 动态数组 ArrayList 与 Vector
1.3 链表LinkedList
2. Map 接口分析
2.1 哈希表的物理结构
2.2 HashMap 中数据添加过程
2.3 LinkedHashMap
一:数据结构
简单来说,数据结构,就是一种程序设计优化的方法论,研究数据的逻辑结构和物理结构以及它们之间相互关系,并对这种结构定义相应的运算,目的是加快程序的执行速度、减少内存占用的空间。
1. 数据结构剖析
1.1 研究对象一:数据间逻辑关系
数据的逻辑结构指反映数据元素之间的逻辑关系,而与数据的存储无关,是独立于计算机的
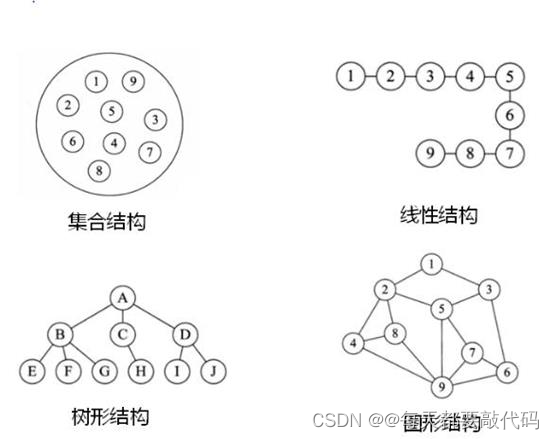
集合结构:数据结构中的元素之间除了“同属一个集合” 的相互关系外,别无其他关系。集合元素之间没有逻辑关系。
线性结构:数据结构中的元素存在一对一的相互关系。比如:排队。结构中必须存在唯一的首元素和唯一的尾元素。体现为:一维数组、链表、栈、队列。
树形结构:数据结构中的元素存在一对多的相互关系。比如:家谱、文件系统、组织架构。
图形结构:数据结构中的元素存在多对多的相互关系。比如:全国铁路网、地铁图。
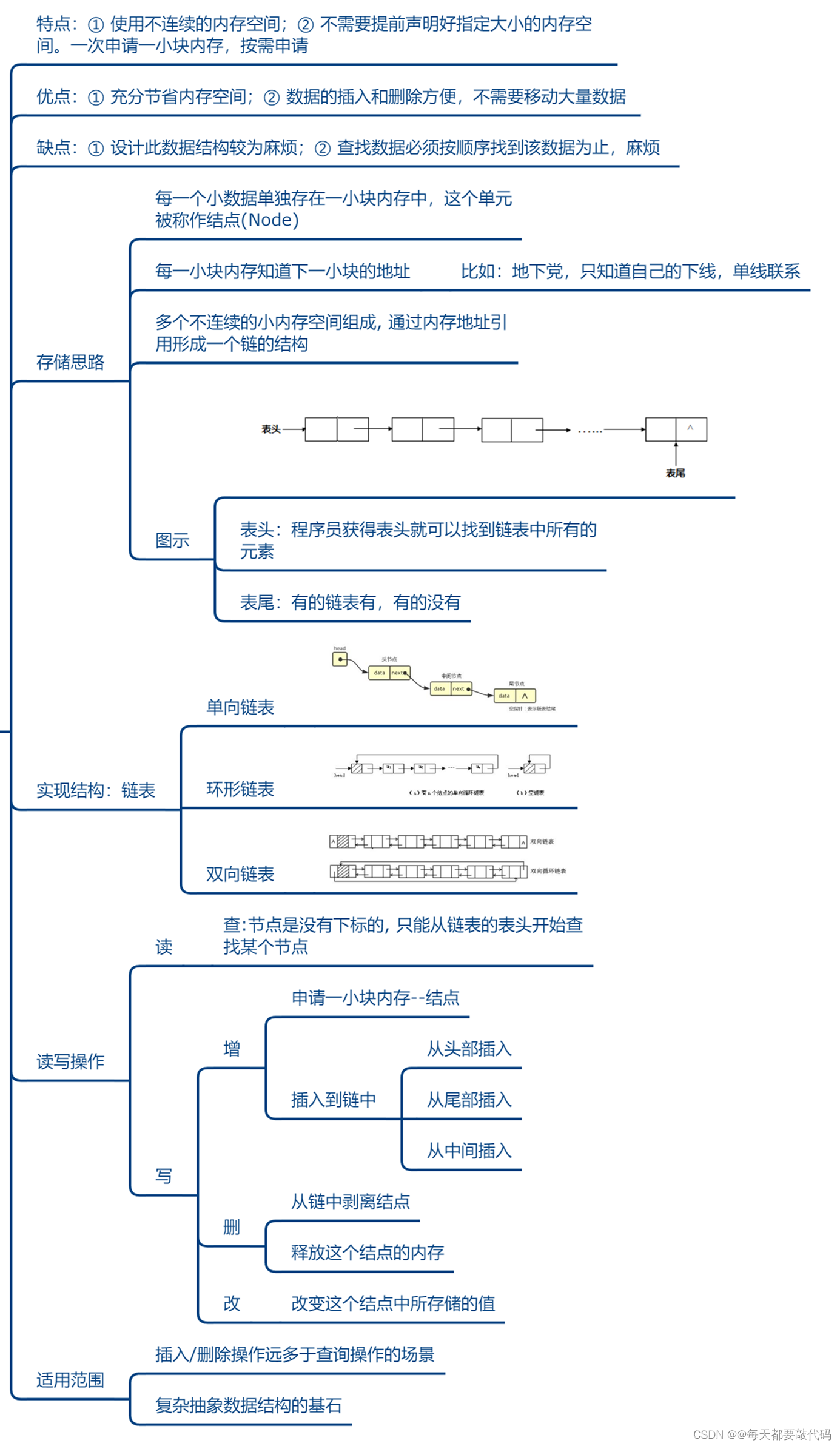
1.2 研究对象二:数据的存储结构(或物理结构)
数据的物理结构/存储结构:包括
数据元素的表示和关系的表示。数据的存储结构是逻辑结构用计算机语言的实现,它依赖于计算机语言。
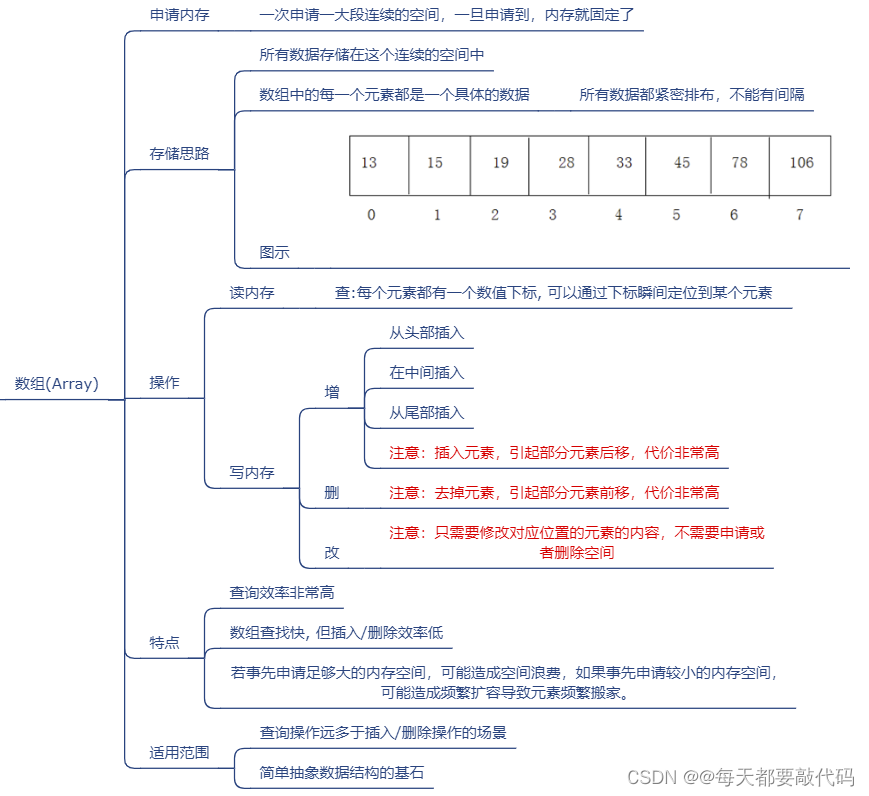
结构1:顺序结构
顺序结构就是使用一组连续的存储单元依次存储逻辑上相邻的各个元素。
优点: 只需要申请存放数据本身的内存空间即可,支持下标访问,也可以实现随机访问。
缺点: 必须静态分配连续空间,内存空间的利用率比较低。插入或删除可能需要移动大量元素,效率比较低。
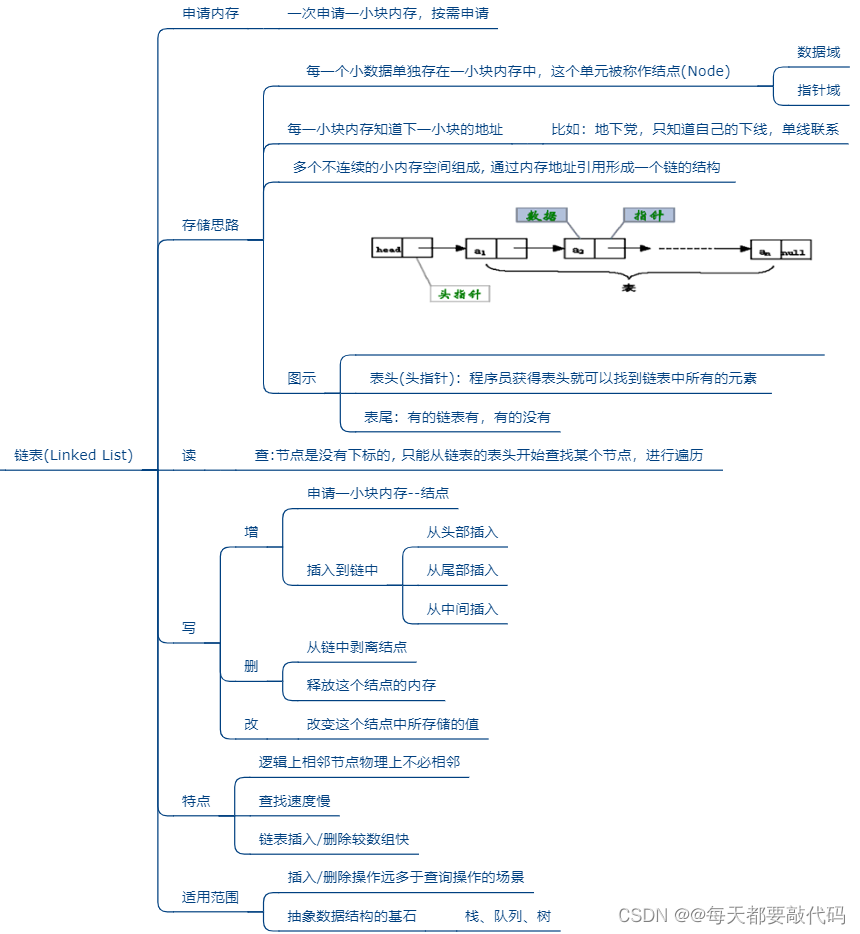
结构2:链式结构
不使用连续的存储空间存放结构的元素,而是为每一个元素构造一个节点。
节点中除了存放数据本身以外,还需要存放指向下一个节点的指针!
优点:不采用连续的存储空间导致内存空间利用率比较高,克服顺序存储结构中预知元素个数的缺点。插入或删除元素时,不需要移动大量的元素。
缺点:需要额外的空间来表达数据之间的逻辑关系,不支持下标访问和随机访问。
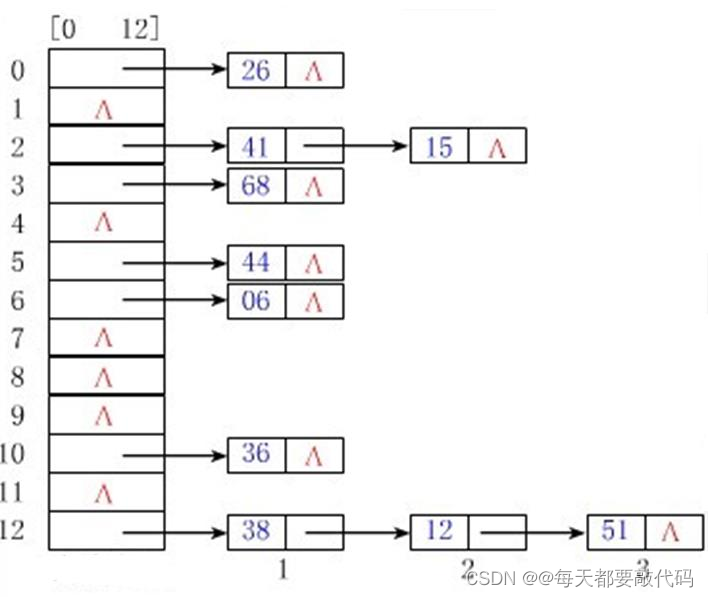
结构3:索引结构
除建立存储节点信息外,还建立附加的索引表来记录每个元素节点的地址。索引表由若干索引项组成。索引项的一般形式是:(关键字,地址)。
优点:用节点的索引号来确定结点存储地址,检索速度快。
缺点: 增加了附加的索引表,会占用较多的存储空间。在增加和删除数据时要修改索引表,因而会花费较多的时间。

结构4:散列结构
根据元素的关键字直接计算出该元素的存储地址,又称为 Hash 存储。
优点:检索、增加和删除结点的操作都很快。
缺点:不支持排序,一般比用线性表存储需要更多的空间,并且记录的关键字不能重 复。
总结:在开发中,习惯上如下的方式理解存储结构
①线性表(一对一关系):一维数组、单向链表、双向链表、栈、队列等。
②树(一对多关系):二叉树、B+树等。
③图(多对多关系)。
④哈希表,比如:HashSet、HashMap等。
1.3 研究对象三:运算结构
施加在数据上的运算包括运算的定义和实现。运算的定义是针对逻辑结构的, 指出运算的功能;运算的实现是针对存储结构的,指出运算的具体操作步骤。
①分配资源,建立结构,释放资源。
②插入和 删除。
③获取 和 遍历。
④修改 和 排序。
2. 常见存储结构之:数组
在 Java 中,数组是用来存放同一种数据类型的集合,注意只能存放同一种数据类型!
//只声明了类型和长度
数据类型[] 数组名称 = new 数据类型[数组长度];
//声明了类型,初始化赋值,大小由元素个数决定
数据类型[] 数组名称 = {数组元素1,数组元素2,......}例如:整型数组

例如:对象数组
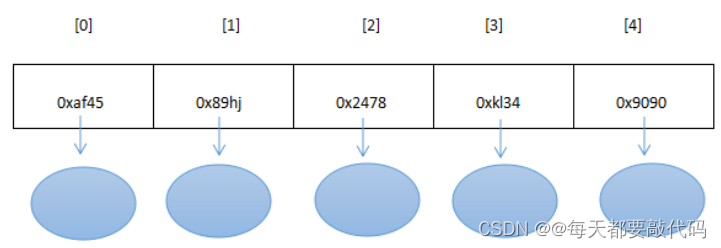
物理结构特点:
①申请内存:一次申请一大段连续的空间,一旦申请到了,内存就固定了。
②不能动态扩展(初始化给大了,浪费;给小了,不够用),插入快,删除和查找慢。
③存储特点:所有数据存储在这个连续的空间中,数组中的每一个元素都是 一个具体的数据(或对象),所有数据都紧密排布,不能有间隔。
具体如下图:

常见的操作:
package com.zl.array;
public class ArrayTest01 {
public static void main(String[] args) {
Array array = new Array(10);
// 添加
array.add(1);
array.add(2);
array.add(3);
array.add(4);
array.add(5);
// 查找
System.out.println(array.find(3)); // 2
// 删除
System.out.println(array.remove(2)); // true
// 打印
array.print(); // 1 3 4 5
}
}
// 自定义数组
class Array{
private Object[] elementData;
private int size;
// 初始化大小
public Array(int capacity) {
elementData = new Object[capacity];
this.size = 0;
}
/**
* 添加元素
*/
public void add(Object value){
if (size >= elementData.length) {
throw new RuntimeException("数组已满,不可添加!");
}
// 把数据放进去
elementData[size] = value;
size++;
}
/**
* 查询元素 value 在数组中的索引位置
*/
public int find(Object value){
for (int i = 0; i < size; i++) {
if (elementData[i].equals(value)){
return i;
}
}
return -1;
}
/**
*从当前数组中移除首次出现的 value 元素
*/
public boolean remove(Object value){
// 查找value对应的下标
int index = find(value);
if (index == -1){
return false;
}
for (int i = index; i < size-1; i++) {
elementData[i] = elementData[i+1];
}
elementData[size-1] = null;
size--;
return true;
}
/**
* 遍历数组中所有数据
*/
public void print(){
for (int i = 0; i < size; i++) {
System.out.print(elementData[i]+"\t");
}
System.out.println();
}
}
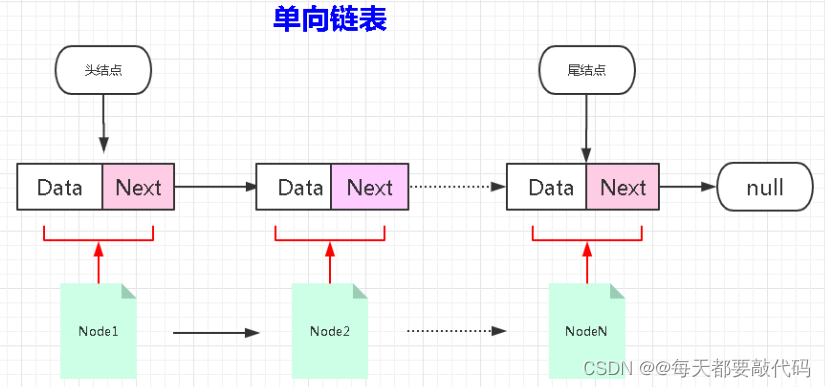
3. 常见存储结构之:链表
①逻辑结构:线性结构。
②物理结构:不要求连续的存储空间。
③存储特点:链表由一系列结点 node(链表中每一个元素称为结点)组成,结点可以在代码执行过程中动态创建。每个结点包括两个部分:一个是存储数据元素的数据域,另一个是存储下一个结点地址的指针域。
常见的链表结构有如下的形式:
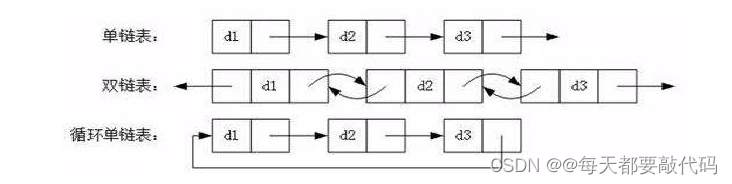
单向链表存储结构图
模拟实现:
package com.zl.array;
public class LinkedTest {
public static void main(String[] args) {
SingleLinked singleLinked = new SingleLinked();
// 添加
singleLinked.add(1);
singleLinked.add(3);
singleLinked.add(2);
// 打印
singleLinked.print();
}
}
// 定义节点
class Node{
// 存储数据
Object data;
// 下一个节点的地址
Node next;
// 构造方法
public Node() {
}
public Node(Object data, Node next) {
this.data = data;
this.next = next;
}
}
// 定义链表
class SingleLinked{
// 头节点
Node header;
// 元素的个数
int size;
// 添加元素
public void add(Object data){
// 如果当前为空,把新添加进来的作为头结点
if (header == null){
header = new Node(data,null);
}else {
// 如果当前非空,根据头结点找到尾结点进行插入操作
Node lastNode = findLastNode(header);
lastNode.next = new Node(data,null);
}
size++;
}
public Node findLastNode(Node node) {
Node cur = node;
while (cur.next != null){
cur = cur.next;
}
return cur;
}
// 打印
public void print(){
Node cur = header;
while (cur != null){
System.out.print(cur.data+"\t");
cur = cur.next;
}
}
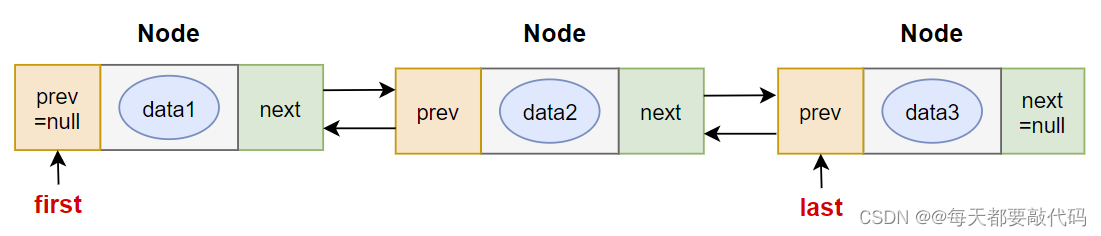
}双向链表存储结构图
4. 常见存储结构之:栈
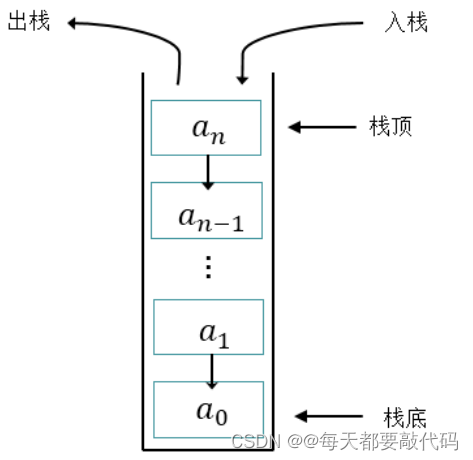
(1)栈(Stack)又称为堆栈或堆叠,是限制仅在表的一端进行插入和删除运算的线性表。
(2)栈按照
先进后出(FILO,first in last out)的原则存储数据,先进入的数据被压入栈底,最后的数据在栈顶。每次删除(退栈)的总是删除当前栈中最后插入(进栈)的元素,而最先插入的是被放在栈的底部,要到最后才能删除。(3)核心类库中的栈结构有Stack和LinkedList。
①Stack就是顺序栈,它是Vector的子类。
②LinkedList是链式栈。
(4)体现栈结构的操作方法:
①peek()方法:查看栈顶元素,不弹出
②pop()方法:弹出栈
③push(E e)方法:压入栈
(5)时间复杂度:
①搜索:
O(n)②插入:
O(1)③移除:
O(1)
图示:
模拟实现
public class MyStack {
private Object[] elements;
private int index;
/**
* 无参数构造方法。默认初始化栈容量10.
*/
public MyStack() {
// 一维数组动态初始化
// 默认初始化容量是10.
this.elements = new Object[10];
// 给index初始化
this.index = -1;
}
/**
* 压栈的方法
* @param obj 被压入的元素
*/
public void push(Object obj) throws Exception {
if(index >= elements.length - 1){
throw new Exception("压栈失败,栈已满!");
}
// 程序能够走到这里,说明栈没满
// 向栈中加1个元素,栈帧向上移动一个位置。
index++;
elements[index] = obj;
System.out.println("压栈" + obj + "元素成功,栈帧指向" + index);
}
/**
* 弹栈的方法,从数组中往外取元素。每取出一个元素,栈帧向下移动一位。
* @return
*/
public Object pop() throws Exception {
if (index < 0) {
//方式2:
throw new Exception("弹栈失败,栈已空!");
}
// 程序能够执行到此处说明栈没有空。
Object obj = elements[index];
System.out.print("弹栈" + obj + "元素成功,");
elements[index] = null;
// 栈帧向下移动一位。
index--;
return obj;
}
// 封装:第一步:属性私有化,第二步:对外提供set和get方法。
public Object[] getElements() {
return elements;
}
public void setElements(Object[] elements) {
this.elements = elements;
}
public int getIndex() {
return index;
}
public void setIndex(int index) {
this.index = index;
}
}5. 常见存储结构之:队列
(1)队列(Queue)是只允许在一端进行插入,而在另一端进行删除的运算受限的线性表。(2) 队列是逻辑结构,其物理结构可以是数组,也可以是链表。
(3)队列的修改原则:队列的修改是依
先进先出(FIFO)的原则进行的。新来的成员总是加入队尾(即不允许"加塞"),每次离开的成员总是队列头上的(不允许中途离队),即当前"最老的"成员离队。
图示: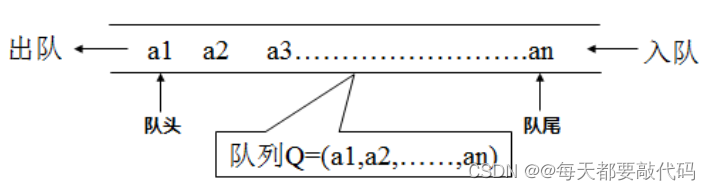
6. 常见存储结构之:树与二叉树
6.1 树的理解
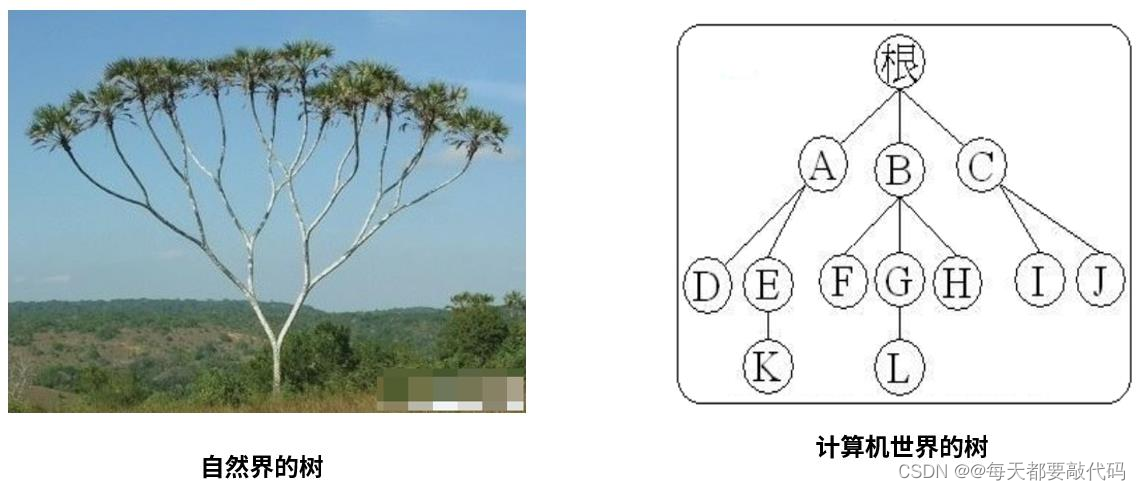
专有名词解释:
结点:树中的数据元素都称之为结点。
根节点:最上面的结点称之为根,一颗树只有一个根且由根发展而来,从另外一个角度来说,每个结点都可以认为是其子树的根。
父节点:结点的上层结点,如图中,结点K的父节点是E、结点L的父节点是G。
子节点:节点的下层结点,如图中,节点E的子节点是K节点、节点G的子节点是L节点。
兄弟节点:具有相同父节点的结点称为兄弟节点,图中F、G、H互为兄弟节点。
结点的度数:每个结点所拥有的子树的个数称之为结点的度,如结点B的度为3。
树叶:度数为0的结点,也叫作终端结点,图中D、K、F、L、H、I、J都是树叶。
非终端节点(或分支节点):树叶以外的节点,或度数不为0的节点。图中根、A、B、C、E、G都是。
树的深度(或高度):树中结点的最大层次数,图中树的深度为4。
结点的层数:从根节点到树中某结点所经路径上的分支树称为该结点的层数,根节点的层数规定为1,其余结点的层数等于其父亲结点的层数+1。
同代:在同一棵树中具有相同层数的节点。
6.2 二叉树的基本概念
二叉树(Binary tree)是树形结构的一个重要类型。二叉树特点是每个结点最多只能有两棵子树,且有左右之分。许多实际问题抽象出来的数据结构往往是二叉树形式,二叉树的存储结构及其算法都较为简单,因此二叉树显得特别重要。

6.3 二叉树的遍历
前序遍历:中左右(根左右)
即先访问根结点,再前序遍历左子树,最后再前序遍历右子 树。前序遍历运算访问二叉树各结点是以根、左、右的顺序进行访问的。
中序遍历:左中右(左根右)
即先中前序遍历左子树,然后再访问根结点,最后再中序遍 历右子树。中序遍历运算访问二叉树各结点是以左、根、右的顺序进行访问的。
后序遍历:左右中(左右根)
即先后序遍历左子树,然后再后序遍历右子树,最后访问根 结点。后序遍历运算访问二叉树各结点是以左、右、根的顺序进行访问的。
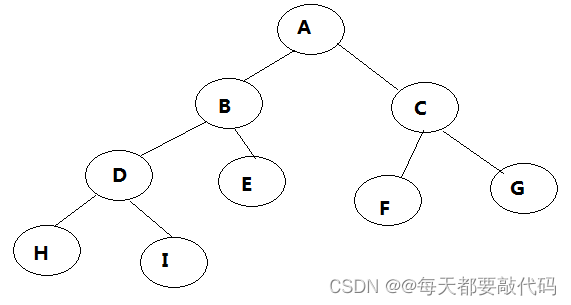
前序遍历:ABDHIECFG
中序遍历:HDIBEAFCG
后序遍历:HIDEBFGCA
6.4 经典二叉树
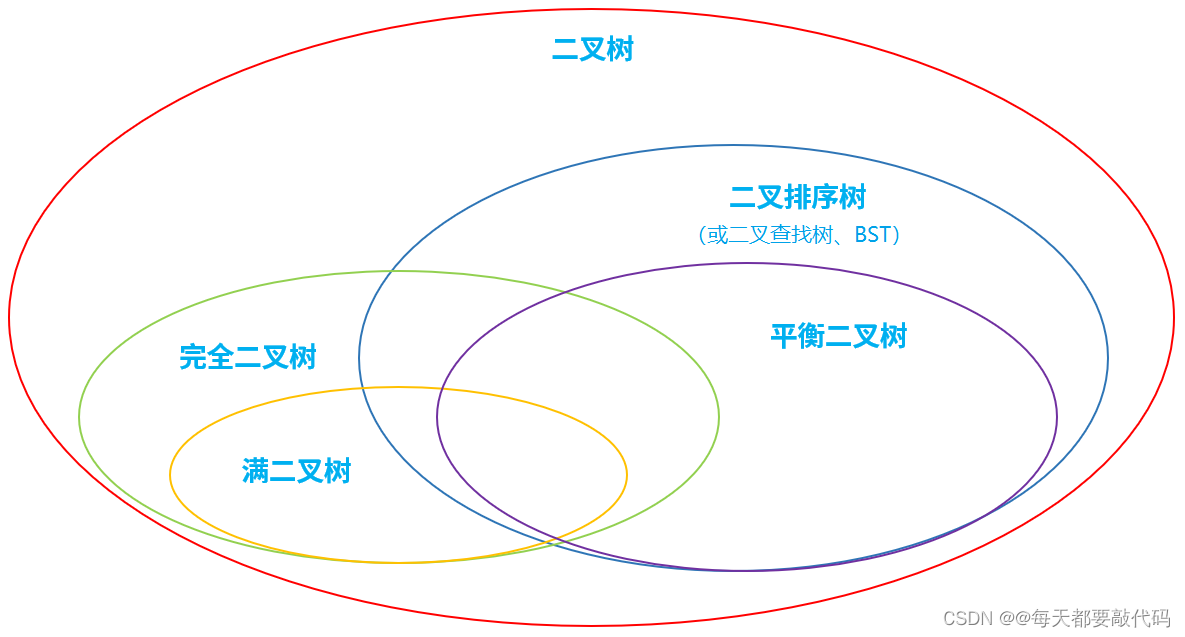
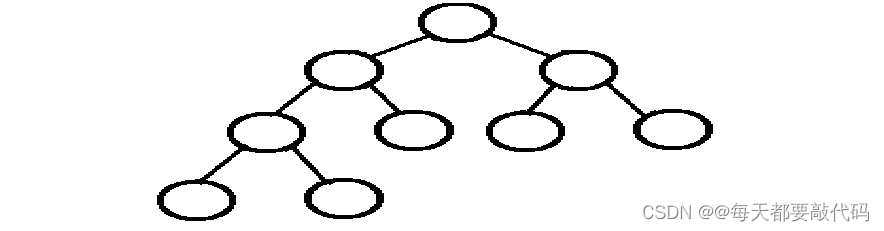
满二叉树
除最后一层无任何子节点外,每一层上的所有结点都有两个子 结点的二叉树。 第 n 层的结点数是 2 的 n-1 次方,总的结点个数是 2 的 n 次方-1
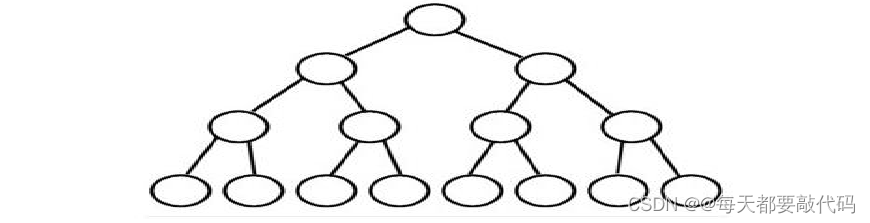
完全二叉树
叶结点只能出现在最底层的两层,且最底层叶结点均处于次 底层叶结点的左侧。
二叉排序/查找/搜索树
即为 BST (binary search/sort tree)。满足如下性质:
(1)若它的左子树不为空,则左子树上所有结点的值均小于它的根节点的值;
(2)若它的右子树上所有结点的值均大于它的根节点的值;
(3)它的左、 右子树也分别为二叉排序/查找/搜索树。
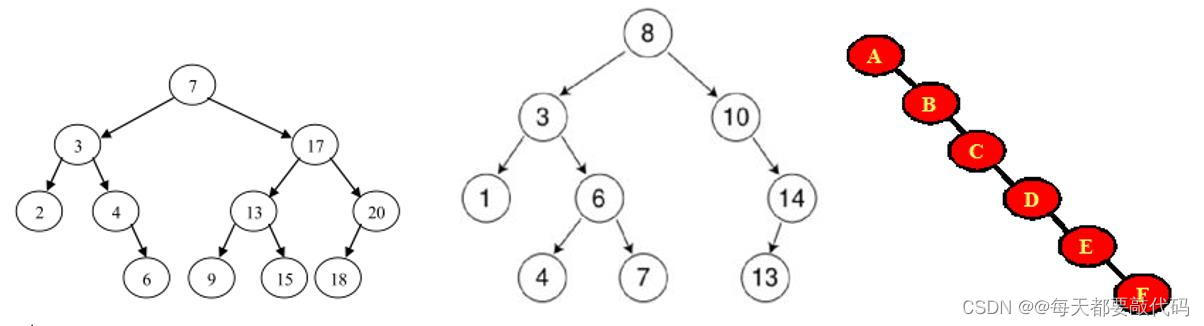
注意:对二叉查找树进行中序遍历,得到有序集合;便于检索。
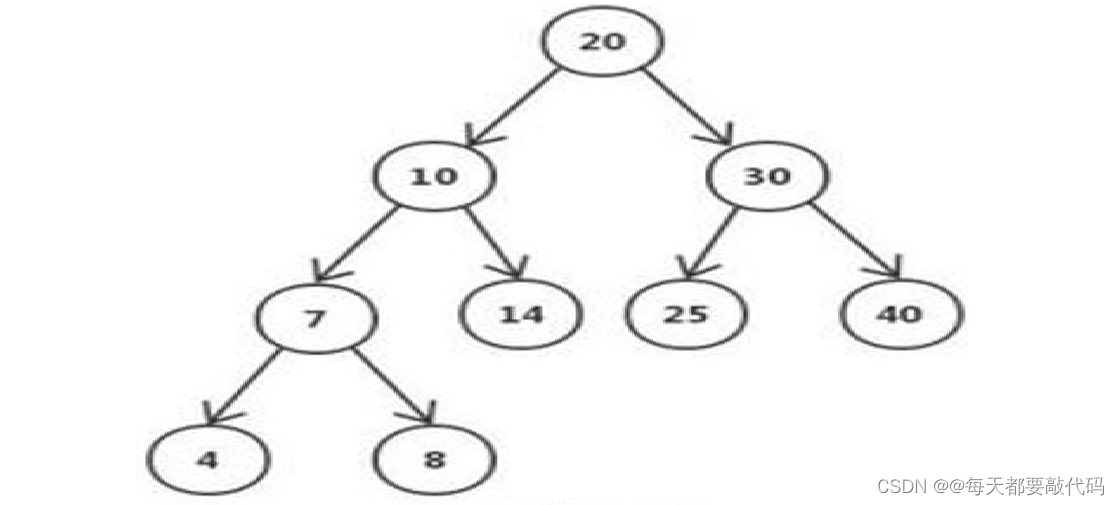
平衡二叉树
(Self-balancing binary search tree,AVL)首先是二叉排序树,此外具有以下性质:
(1)它是一棵空树或它的左右两个子树的高度差的绝对值不超过1 ;
(2)并且左右两个子树也都是一棵平衡二叉树 ;
(3)不要求非叶节点都有两个子结点。
注:平衡二叉树的目的是为了减少二叉查找树的层次,提高查找速度。平衡二叉树的常用实现有红黑树、AVL、替罪羊树、Treap、伸展树等。
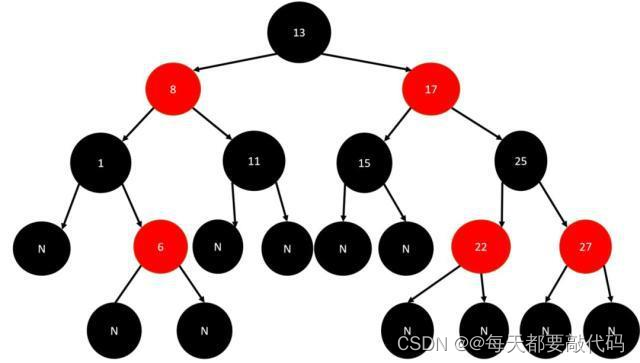
红黑树
即Red-Black Tree。红黑树的每个节点上都有存储位表示节点的颜色,可以是红(Red)或黑(Black)。 红黑树是一种自平衡二叉查找树,是在计算机科学中用到的一种数据结构,它是在 1972 年由 Rudolf Bayer 发明的。红黑树是复杂的,但它的操作有着
良好的最坏情况运行时间,并且在实践中是高效的:它可以在 O(log n)时间内做查找,插入和删除, 这里的 n 是树中元素的数目。
红黑树的特性:
①每个节点是红色或者黑色。
②根节点是黑色。
③每个叶子节点(NIL)是黑色。(注意:这里叶子节点,是指为空(NIL或NULL)的叶子节点)。
④每个红色节点的两个子节点都是黑色的。(从每个叶子到根的所有路径上不能有两个连续的红色节点)。
⑤从任一节点到其每个叶子的所有路径都包含相同数目的黑色节点(确保没有一条路径会比其他路径长出2倍)。
当我们插入或删除节点时,可能会破坏已有的红黑树,使得它不满足以上5个要求,那么此时就需要进行处理,使得它继续满足以上的5个要求:
①recolor:将某个节点变红或变黑。②
rotation:将红黑树某些结点分支进行旋转(左旋或右旋)。
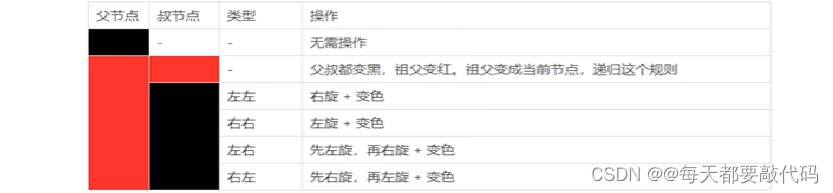
红黑树可以通过红色节点和黑色节点尽可能的保证二叉树的平衡。主要是用它来存储有序的数据,它的时间复杂度是 O(logN),效率非常之高!
二:常用集合的源码分析
1. List 接口分析
1.1 List接口特点
(1)List集合所有的元素是以一种
线性方式进行存储的,例如,存元素的顺序是11、22、33。那么集合中,元素的存储就是按照11、22、33的顺序完成的)。(2)它是一个元素
存取有序的集合。即元素的存入顺序和取出顺序有保证。(3)它是一个
带有索引的集合,通过索引就可以精确的操作集合中的元素(与数组的索引是一个道理)。(4)集合中可以有
重复的元素,通过元素的equals方法,来比较是否为重复的元素。

注意:List 集合关心元素是否有序,而不关心是否重复!
List 接口的主要实现类:
– ArrayList:动态数组;
– Vector:动态数组;
– LinkedList:双向链表;
– Stack:栈 ;
1.2 动态数组 ArrayList 与 Vector
Java 的 List 接口的实现类中有两个动态数组的实现:ArrayList 和 Vector!
(1)ArrayList 与 Vector 的区别
它们的底层物理结构都是数组,我们称为动态数组!
①ArrayList是新版的动态数组,线程不安全,效率高,Vector是旧版的动态数组,线程安全,效率低。
②动态数组的扩容机制不同,ArrayList默认扩容为原来的1.5倍,Vector默认扩容增加为原来的2倍。
③数组的初始化容量,如果在构建ArrayList与Vector的集合对象时,没有显式指定初始化容量,那么Vector的内部数组的初始容量默认为10,而ArrayList在JDK 6.0 及之前的版本也是10,JDK8.0 之后的版本ArrayList初始化为长度为0的空数组,之后在添加第一个元素时,再创建长度为10的数组。原因: 用的时候,再创建数组,避免浪费。因为很多方法的返回值是ArrayList类型,需要返回一个ArrayList的对象 ,例如:后期从数据库查询对象的方法,返回值很多就是ArrayList。有可能你要查询的数据不存在,要么返回null,要么返回一个没有元素的ArrayList对象。
(2)ArrayList部分源码分析
JDK7中:
①实例化对象时
在new ArrayList()集合时,底层实际上会初始化一个长度为10的Object数组:
ArrayList<String> list = new ArrayList<>();
// 就等价于
Object[] elementData = new Object[10];②调用add方法时
当调用add方法时,底层实际上会给Object的数组进行赋值操作
list.add("AA");
// 就等价于
elementData[0] = "AA";③需要扩容时
当要添加第11个元素时,底层的elementData数组已满,则需要扩容;默认扩容为原来的1.5倍
// 扩容到原来的1.5倍
int newCapacity = oldCapacity + (oldCapacity >> 1); 并将原有数组中的元素复制到新的数组中
//复制一个新数组
elementData = Arrays.copyOf(elementData, newCapacity);jdk8中:
①在JDK8中,实例化时也会创建一个Object数组,只不过创建是长度为0的数组
ArrayList<String> list = new ArrayList<>();
// 就等价于
Object[] elementData = new Object[]{}; // 静态初始化一个长度为0的数组 ②首次调用add方法,添加元素时,会先初始化数组的长度为10,然后在进行元素的添加
// 第一步
elementData = new Object[10];
// 第二步
elementData[0] = "AA";总结:在JDK7之前,ArrayList类似于单例模式中的饿汉式,上来就把对象创建好。在JDK8之后,ArrayList类似于单例模式中的懒汉式,需要的时候我再去创建!对于Vector集合来说,也是初始化为长度为10的Object数组,但是扩容是原来的2倍!
1.3 链表LinkedList
Java中有双链表的实现:LinkedList,它是List接口的实现类。
LinkedList是一个双向链表,如图所示:
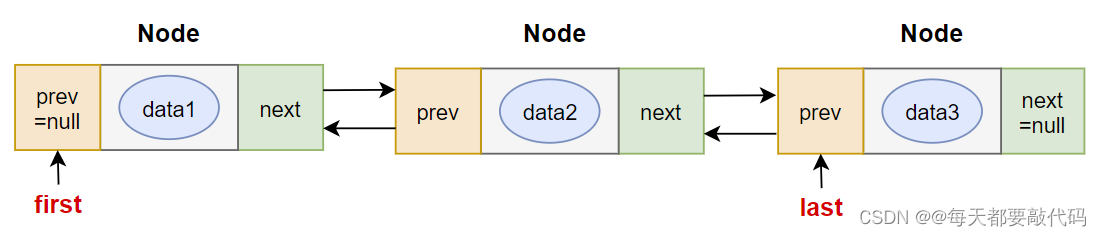
链表与动态数组的区别
①动态数组底层的物理结构是数组,因此根据索引访问的效率非常高。但是非末尾位置的插入和删除效率不高,因为涉及到移动元素。另外添加操作时涉及到扩容问题,就会增加时空消耗。
②链表底层的物理结构是链表,因此根据索引访问的效率不高,即查找元素慢。但是插入和删除不需要移动元素,只需要修改前后元素的指向关系即可,所以插入、删除元素快。而且链表的添加不会涉及到扩容问题。
LinkedList源码分析
//属性
transient Node<E> first; //记录第一个结点的位置
transient Node<E> last; //记录当前链表的尾元素
transient int size = 0; //记录最后一个结点的位置
//构造器
public LinkedList() {
}
//方法:add()相关方法
public boolean add(E e) {
linkLast(e); //默认把新元素链接到链表尾部
return true;
}
void linkLast(E e) {
final Node<E> l = last; //用 l 记录原来的最后一个结点
//创建新结点
final Node<E> newNode = new Node<>(l, e, null);
//现在的新结点是最后一个结点了
last = newNode;
//如果l==null,说明原来的链表是空的
if (l == null)
//那么新结点同时也是第一个结点
first = newNode;
else
//否则把新结点链接到原来的最后一个结点的next中
l.next = newNode;
//元素个数增加
size++;
//修改次数增加
modCount++;
}
//其中,Node类定义如下
private static class Node<E> {
E item; //元素数据
Node<E> next; //下一个结点
Node<E> prev; //前一个结点
Node(Node<E> prev, E element, Node<E> next) {
this.item = element;
this.next = next;
this.prev = prev;
}
}
//方法:获取get()相关方法
public E get(int index) {
checkElementIndex(index);
return node(index).item;
}
//方法:插入add()相关方法
public void add(int index, E element) {
checkPositionIndex(index);//检查index范围
if (index == size)//如果index==size,连接到当前链表的尾部
linkLast(element);
else
linkBefore(element, node(index));
}
Node<E> node(int index) {
// assert isElementIndex(index);
/*
index < (size >> 1)采用二分思想,先将index与长度size的一半比较,如果index<size/2,就只从位置0
往后遍历到位置index处,而如果index>size/2,就只从位置size往前遍历到位置index处。这样可以减少一部
分不必要的遍历。
*/
//如果index<size/2,就从前往后找目标结点
if (index < (size >> 1)) {
Node<E> x = first;
for (int i = 0; i < index; i++)
x = x.next;
return x;
} else {//否则从后往前找目标结点
Node<E> x = last;
for (int i = size - 1; i > index; i--)
x = x.prev;
return x;
}
}
//把新结点插入到[index]位置的结点succ前面
void linkBefore(E e, Node<E> succ) {//succ是[index]位置对应的结点
// assert succ != null;
final Node<E> pred = succ.prev; //[index]位置的前一个结点
//新结点的prev是原来[index]位置的前一个结点
//新结点的next是原来[index]位置的结点
final Node<E> newNode = new Node<>(pred, e, succ);
//[index]位置对应的结点的prev指向新结点
succ.prev = newNode;
//如果原来[index]位置对应的结点是第一个结点,那么现在新结点是第一个结点
if (pred == null)
first = newNode;
else
pred.next = newNode;//原来[index]位置的前一个结点的next指向新结点
size++;
modCount++;
}
//方法:remove()相关方法
public boolean remove(Object o) {
//分o是否为空两种情况
if (o == null) {
//找到o对应的结点x
for (Node<E> x = first; x != null; x = x.next) {
if (x.item == null) {
unlink(x);//删除x结点
return true;
}
}
} else {
//找到o对应的结点x
for (Node<E> x = first; x != null; x = x.next) {
if (o.equals(x.item)) {
unlink(x);//删除x结点
return true;
}
}
}
return false;
}
E unlink(Node<E> x) {//x是要被删除的结点
// assert x != null;
final E element = x.item;//被删除结点的数据
final Node<E> next = x.next;//被删除结点的下一个结点
final Node<E> prev = x.prev;//被删除结点的上一个结点
//如果被删除结点的前面没有结点,说明被删除结点是第一个结点
if (prev == null) {
//那么被删除结点的下一个结点变为第一个结点
first = next;
} else {//被删除结点不是第一个结点
//被删除结点的上一个结点的next指向被删除结点的下一个结点
prev.next = next;
//断开被删除结点与上一个结点的链接
x.prev = null;//使得GC回收
}
//如果被删除结点的后面没有结点,说明被删除结点是最后一个结点
if (next == null) {
//那么被删除结点的上一个结点变为最后一个结点
last = prev;
} else {//被删除结点不是最后一个结点
//被删除结点的下一个结点的prev执行被删除结点的上一个结点
next.prev = prev;
//断开被删除结点与下一个结点的连接
x.next = null;//使得GC回收
}
//把被删除结点的数据也置空,使得GC回收
x.item = null;
//元素个数减少
size--;
//修改次数增加
modCount++;
//返回被删除结点的数据
return element;
}
public E remove(int index) { //index是要删除元素的索引位置
checkElementIndex(index);
return unlink(node(index));
}2. Map 接口分析
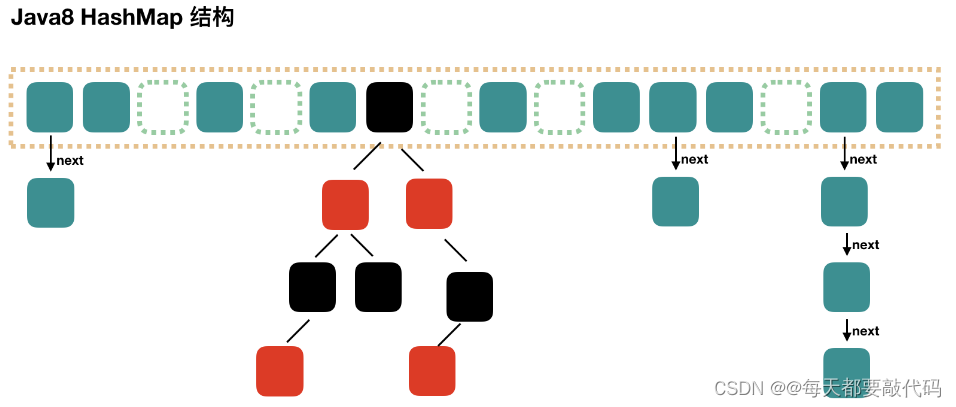
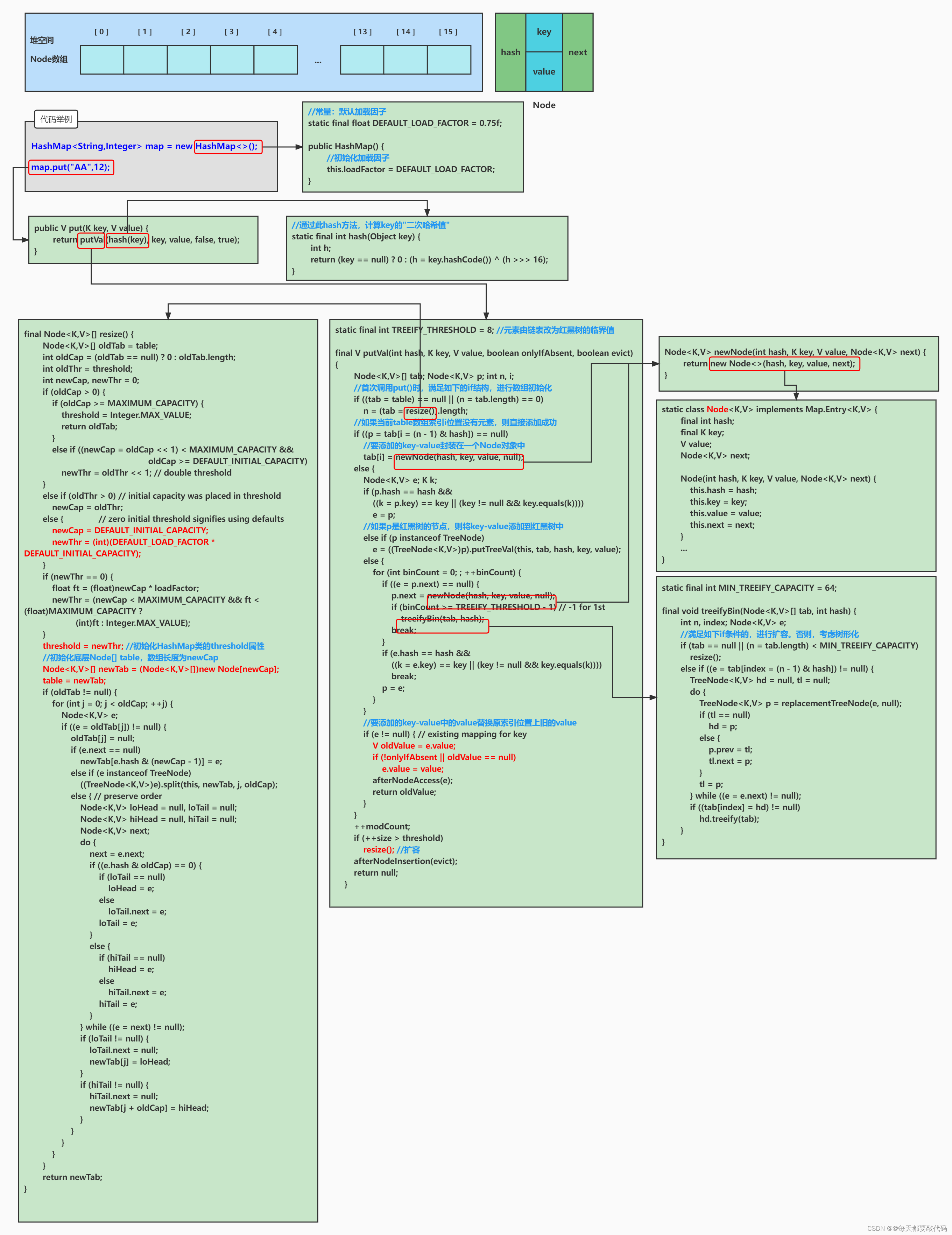
2.1 哈希表的物理结构
HashMap和Hashtable底层都是哈希表(也称散列表),其中维护了一个长度为2的幂次方的Entry类型的数组table,数组的每一个索引位置被称为一个桶(bucket),添加的映射关系(key,value)最终都被封装为一个Map.Entry类型的对象,放到某个table[index]桶中。
使用数组的目的是查询和添加的效率高,可以根据索引直接定位到某个table[index]
2.2 HashMap 中数据添加过程
JDK7中:
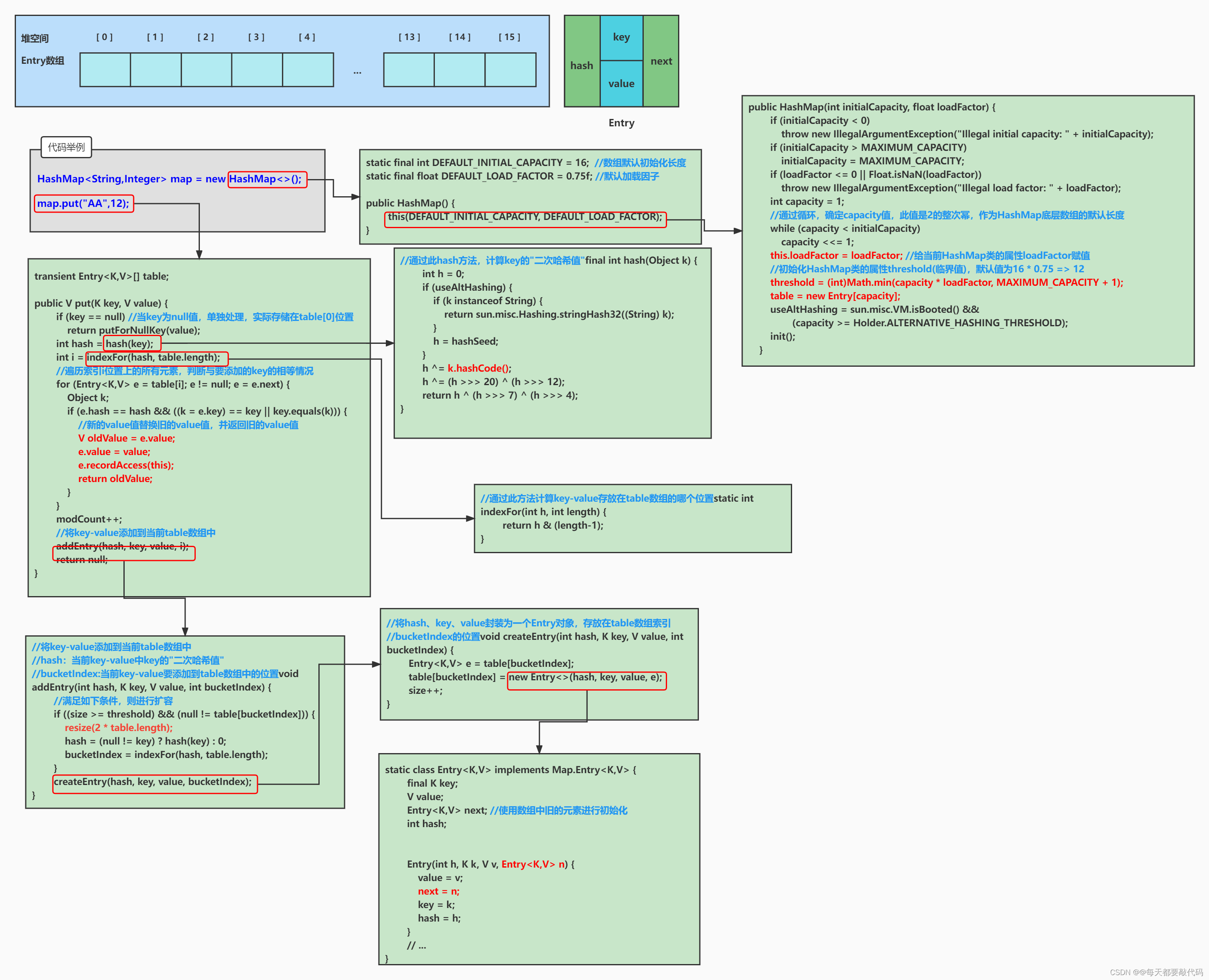
(1)HashMap map = new HashMap();底层实际上创建了一个长度为16的Entry[]的数组Entry[] table = new Entry[16];
(2)map.put(key1,value1); 将(key1,value1)添加到当前 hashmap 的对象中。首先会调用 key1 所在类的 hashCode()方法,计算 key1 的哈希值1,此哈希值1 再经过某种运算(hash()方法),得到哈希值 2。此哈希值2 再经过某种运算(indexFor()方法),确定在底层 table 数组中的索引位置 i。
①如果数组索引为 i 上的数据为空,则(key1,value1)直接添加成功------位置 1;
②如果数组索引为 i 上的数据不为空,有(key2,value2),则需要进一步判断:判断 key1 的哈希值 2 与 key2 的哈希值是否相同:
③如果哈希值不同,则(key1,value1)直接添加成功 ------位置 2;如果哈希值相同,则需要继续调用 key1 所在类的 equals()方法,将key2 放入 equals()形参进行判断:
④equals 方法返回 false : 则(key1,value1)直接添加成功------位置 3;equals 方法返回 true : 默认情况下,value1 会覆盖 value2。
(3)位置 1:直接将(key1,value1)以 Entry 对象的方式存放到 table 数组索引 i 的位 置。
(4)位置 2、位置 3:(key1,value1) 与现有的元素以链表的方式存储在 table 数组索引i 的位置,新添加的元素指向旧添加的元素(JDK7是头插法)。
(5)在不断的添加的情况下,满足如下条件的情况下,会进行扩容:
if ((size >= threshold) && (null != table[bucketIndex]))默认情况下,当要添加的元素个数超过 12(即:数组的长度 * loadFactor【加载因子75%】 得到的结果)时,就要考虑扩容。
(6)Entry的结构如下:
static class Entry<K,V> implements Map.Entry<K,V> {
final K key;
V value;
Entry<K,V> next;
int hash; //使用key得到的哈希值2进行赋值。
/**
* Creates new entry.
*/
Entry(int h, K k, V v, Entry<K,V> n) {
value = v;
next = n;
key = k;
hash = h;
}
}
JDK8中:
JDK8相较于JDK7的不同之处:
① 在jdk8中,当我们创建了HashMap实例以后,底层并没有初始化table数组。当首次添加(key,value)时,进行判断,如果发现table尚未初始化,则对数组进行初始化。
② 在jdk8中,HashMap底层定义了Node内部类,替换jdk7中的Entry内部类。意味着,我们创建的数组是Node[]。
③ 在jdk8中,如果当前的(key,value)经过一系列判断之后,可以添加到当前的数组角标i中。如果此时角标i位置上有元素。在jdk7中是将新的(key,value)指向已有的旧的元素(头插法),而在jdk8中是旧的元素指向新的 (key,value)元素(尾插法)。 "七上八下"
④ jdk7:数组+单向链表;jk8:数组+单向链表 + 红黑树
什么时候会使用单向链表变为红黑树?如果数组索引i位置上的元素的个数达到8,并且数组的长度达到64时,我们就将此索引i位置上的多个元素改为使用红黑树的结构进行存储。(为什么修改?红黑树进行put/get/remove操作的时间复杂度为O(logn),比单向链表的时间复杂度O(n)的好,性能更高。
什么时候会使用红黑树变为单向链表?
当使用红黑树的索引i位置上的元素的个数低于6的时候,就会将红黑树结构退化为单向链表
2.3 LinkedHashMap
LinkedHashMap 是 HashMap的子类; LinkedHashMap在HashMap使用的数组+单向链表+红黑树的基础上,又增加了一对双向链表,记录添加的(key,value)的先后顺序;便于我们遍历所有的key-value。
通过源码发现当调用put方法时,实际上调用的还是HashMap的put方法,直到得到了哈希值1、哈希值2,最终获得数组下标真正添加的时候,才会调用一个方法newNode
// LinkedHashMap重写了HashMap的如下方法
Node<K,V> newNode(int hash, K key, V value, Node<K,V> e) {
LinkedHashMap.Entry<K,V> p = new LinkedHashMap.Entry<K,V>(hash, key, value, e);
linkNodeLast(p);
return p;
}而newNode方法又调用了LinkedHashMap的Entry方法,说明内部有一个Entry
2. 底层结构:LinkedHashMap内部定义了一个Entry
static class Entry<K,V> extends HashMap.Node<K,V> {
Entry<K,V> before, after; //增加的一对双向链表
Entry(int hash, K key, V value, Node<K,V> next) {
super(hash, key, value, next);
}
}
面试经典例题
①首先把p1元素添加进去,是根据1001和“AA”计算得到的hash值;p2元素添加时是根据1002和“BB”计算得到的hash值。
②当把p1.name修改为“CC”,此时再去remove(删除)p1,是无法删除的,因为此时删除是1001和“CC”得到的hash值进行删除,和原来的1001和“AA”计算得到的hash值是不同的!
③此时添加new Person(1001,"CC")时可以添加进去的,虽然此时有这个元素,但是当时是根据1001和“AA”计算得到的hash值添加进去的,只不过后来把p1.name改成了“CC”。而此时是添加就是根据1001和“CC”进行添加进去,是可以添加的!
④new Person(1001,"AA")也是可以添加进去的,虽然此时得到的hash值与前面是相同的,此时就需要调用equals方法,原来是1001和“CC”,现在是1001和“AA”,不相同,添加成功!
package com.atguigu03.map.interview;
import java.util.HashSet;
// Person已重写了HashCode方法和equals方法
public class HashSetDemo {
public static void main(String[] args) {
HashSet set = new HashSet();
Person p1 = new Person(1001,"AA");
Person p2 = new Person(1002,"BB");
set.add(p1);
set.add(p2);
System.out.println(set);
p1.name = "CC";
set.remove(p1);
System.out.println(set);
set.add(new Person(1001,"CC"));
System.out.println(set);
set.add(new Person(1001,"AA"));
System.out.println(set);
}
}
执行结果: