1.实验目的:
深刻理解回溯法的基本思想,掌握回溯法解决问题的一般步骤,学会使用回溯法解决实际问题.运用所熟悉的编程工具,借助回溯法的思想求解子集和数的问题。
2.实验内容:
给定 n n n 个正整数 { x 1 , x 2 , ⋯ , x n } \{x_1, x_2, \cdots, x_n\} {x1,x2,⋯,xn},以及一个整数 m m m,判定是否可以从 n n n 个数中取出若干个数,使它们的和等于 m m m。输出: Y E S YES YES或者 N O NO NO。
3.实验要求:
编制程序并对其时间复杂度和空间复杂度进行分析。
□ \square □ 基础性实验 □ \square □ 综合性实验 ⊠ \boxtimes ⊠ 设计性实验
一、问题分析(模型、算法设计和正确性证明等)
对每个整数有取或不取两种选择,判断是否存在一种选取方案是的所选元素之和为给定值 m m m。
方法一:回溯法
在此借用课件中的完全二叉树作为问题规模 n = 3 n=3 n=3的解空间示例,由图可知,回溯的方法可以遍历所有子集判断是否存在一个子集使得其元素和为 m m m。
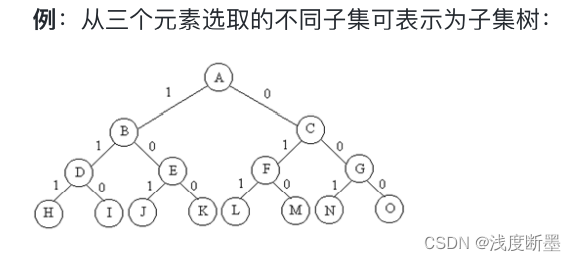
约束条件: ∑ a ∈ S a = m \sum_{a\in S}{a}=m ∑a∈Sa=m,其中 S S S为原集合的子集
剪枝:
- 当前和加剩余元素最小值大于 m m m
- 当前和加剩余元素之和小于 m m m
方法二:动态规划
类似01背包问题,令
f
[
i
]
[
j
]
f[i][j]
f[i][j]表示前
i
i
i个数能否取出和为
j
j
j的子集,则有转移方程:
f
[
0
]
[
0
]
=
1
f
[
i
]
[
j
]
=
m
a
x
(
f
[
i
−
1
]
[
j
]
,
f
[
i
]
[
j
−
a
[
i
]
]
)
f[0][0] = 1\\ f[i][j] = max(f[i-1][j], f[i][j-a[i]])
f[0][0]=1f[i][j]=max(f[i−1][j],f[i][j−a[i]])
可化简为:
f
[
0
]
=
0
f
[
j
]
=
m
a
x
(
f
[
j
]
,
f
[
j
−
a
[
i
]
]
)
f[0]=0\\ f[j] = max(f[j], f[j-a[i]])
f[0]=0f[j]=max(f[j],f[j−a[i]])
二、算法设计复杂度分析(伪代码,不要粘贴源码)
回溯法伪代码:

回溯法复杂度: T ( n ) ∈ O ( 2 n ) T(n) \in O (2^n) T(n)∈O(2n)
动态规划伪代码:

动态规划复杂度: T ( n ) ∈ θ ( n m ) T(n) \in \theta (nm) T(n)∈θ(nm)
三、实验结果记录和分析(测试向量上的测试结果、运行时间)
回溯法运行时间:

动态规划运行时间:
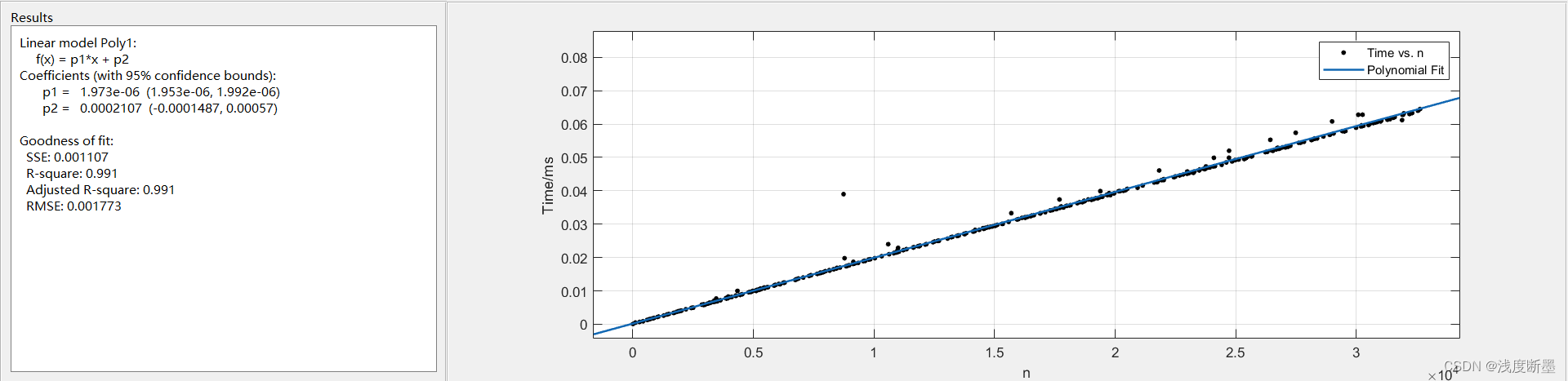
显然动态规划算法在运行时间上的波动程度小于回溯法,且相同规模下运行时间远远小于回溯法。可见回溯法在问题规模较小的情况下有程序编写便捷性和准确性,但是只是在枚举的基础上对一些情况做出特殊处理来降低复杂度,本质上不改变算法复杂度。且回溯法对算法的优化依赖于输入数据,上图中可以看到问题规模相似的情况下运行时间差别仍然较大。
四、总结(可描述出现的问题和解决方法、经验和反思等)
剪枝的方法一定程度上消减了回溯法递归的时间复杂度,但是仍无法影响最坏情况。源程序见CODE文件夹,包括两种算法程序DfsAndDp.cpp,及随机输入数据生成程序generateData.cpp等。