一、概述

1.1概念（树形结构）

1.2区别

1.3步骤

1.4回溯法模板

1.5应用

1.6回溯三部曲

二、组合问题

2.1组合

回溯算法

优化剪枝操作

2.2组合总和

2.3组合总和2

2.4组合总和3

2.5电话号码的字母组合

三、切割问题

3.1分割回文串

3.2.复原IP地址

四、子集问题

4.1子集

4.2子集2

4.3递增子序列

五、排列问题

5.1全排列

5.2全排列 II

六、棋盘问题

6.1N皇后

6.2解数独

一、概述

1.1概念（树形结构）

回溯算法是一种系统地搜索问题的解的方法。某个问题的所有可能解的称为问题的解空间，若解空间是有限的，则可将解空间映射成树结构。回溯算法的基本思想是：从一条路往前走，能进则进，不能进则退回来，换一条路再试。

回溯是递归的副产品，只要有递归就会有回溯。

回溯法就是暴力搜索，并不是什么高效的算法，最多在剪枝一下。

1.2区别

回溯算法和深度优先搜索（DFS）有很多相似之处，但也有不同之处。回溯算法在搜索过程中寻找问题的解，当发现已不满足求解条件时，就“回溯”返回，尝试别的路径。而DFS则是在搜索过程中遍历所有可能的路径，直到找到问题的解

1.3步骤

状态表示：需要定义状态表示方式，以便在搜索过程中能够正确地扩展状态。
决策生成：需要确定当前状态下的所有可能决策，以便进行进一步的搜索。
解空间剪枝：需要根据问题的特点，对搜索过程中无用的状态进行剪枝，以提高算法效率。
解的输出：需要根据问题的要求，确定如何输出符合要求的解。

1.4回溯法模板

result = []
def backtrack(路径, 选择列表):
    if 满足结束条件:
        result.add(路径)
        return
    for 选择 in 选择列表:
        做选择
        backtrack(路径, 选择列表)
        撤销选择

其中，result 存储结果，backtrack 是回溯函数，路径 是已经做出的选择，选择列表 是当前可以做出的选择。

1.5应用

组合问题：N个数里面按一定规则找出k个数的集合
排列问题：N个数按一定规则全排列，有几种排列方式
切割问题：一个字符串按一定规则有几种切割方式
子集问题：一个N个数的集合里有多少符合条件的子集
棋盘问题：N皇后，解数独等等。

1.6回溯三部曲

回溯算法三部曲是指：1. 确定递归函数的参数和返回值；2. 确定终止条件；3. 确定单层搜索的过程。回溯算法是一种暴力搜索算法，它通过不断地尝试所有可能的结果来解决问题。在回溯算法中，我们需要对每个可能的结果进行判断，如果符合条件就加入到结果集中，否则就回溯到上一步，继续尝试其他可能的结果。

二、组合问题

2.1组合

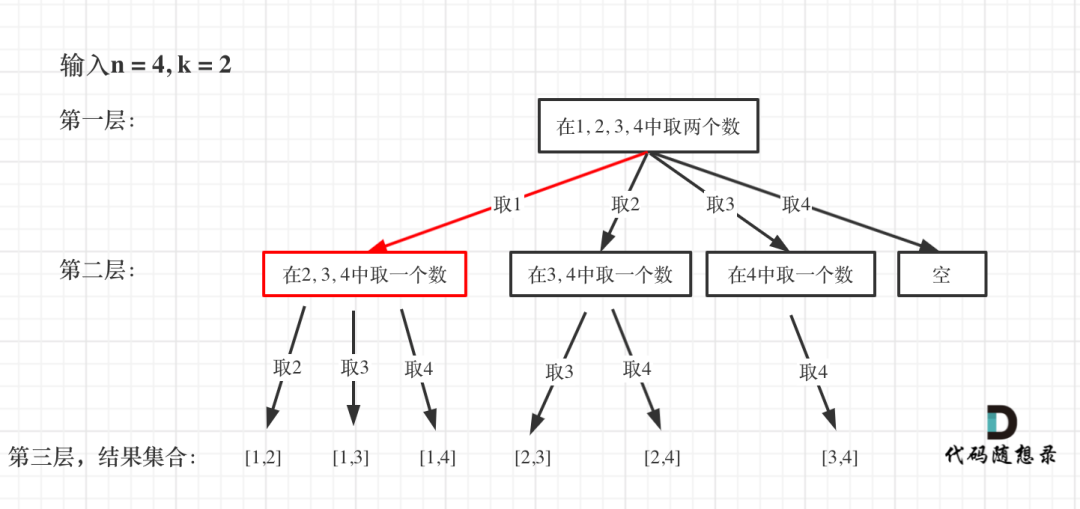
给定两个整数 n 和 k，返回范围 [1, n] 中所有可能的 k 个数的组合。

你可以按任何顺序返回答案。

示例 1：

输入：n = 4, k = 2
输出：
[
[2,4],
[3,4],
[2,3],
[1,2],
[1,3],
[1,4],
]

#include<stdio.h>
#include <iostream>

using namespace std;

const int N = 100;
int a[N];
int n, k;
void dfs(int cur, int cnt) {
    if (cnt == k) {
        for (int i = 0; i < k; i++) {
            cout << a[i] << " ";
        }
        cout << endl;
        return;
    }
    for (int i = cur; i <= n; i++) {
        a[cnt] = i;
        dfs(i + 1, cnt + 1);
    }
}
int main() {
    cin >> n >> k;
    dfs(1, 0);
    return 0;
}

回溯算法

import java.util.*;

public class Solution {

    // 回溯函数
    private void backtracking(List<List<Integer>> result, List<Integer> path, int n, int k, int startIndex) {
        if (path.size() == k) { // 如果path中的元素个数等于k，说明找到了一组符合条件的组合
            result.add(new ArrayList<>(path)); // 将该组合加入结果集中
            return; // 返回上一层递归
        }
        // 枚举所有可能的数
        for (int i = startIndex; i <= n; i++) {
            path.add(i); // 将当前数加入path中，进行处理
            backtracking(result, path, n, k, i + 1); // 递归处理下一个数
            path.remove(path.size() - 1); // 撤销处理的数，回溯到上一层状态
        }
    }

    // 组合函数
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> result = new ArrayList<>(); // 存储符合条件的结果集
        List<Integer> path = new ArrayList<>(); // 存储符合条件的组合
        backtracking(result, path, n, k, 1); // 开始回溯，从数字1开始
        return result; // 返回结果集
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); // 获取用户输入的n
        int k = scanner.nextInt(); // 获取用户输入的k
        scanner.close(); // 关闭Scanner
        Solution solution = new Solution(); // 创建Solution对象
        List<List<Integer>> result = solution.combine(n, k); // 调用组合函数，得到符合条件的结果集
        for (List<Integer> list : result) { // 遍历结果集
            for (int num : list) { // 遍历组合
                System.out.print(num + " "); // 输出组合中的元素
            }
            System.out.println(); // 输出换行，用于分隔每个组合
        }
    }
}

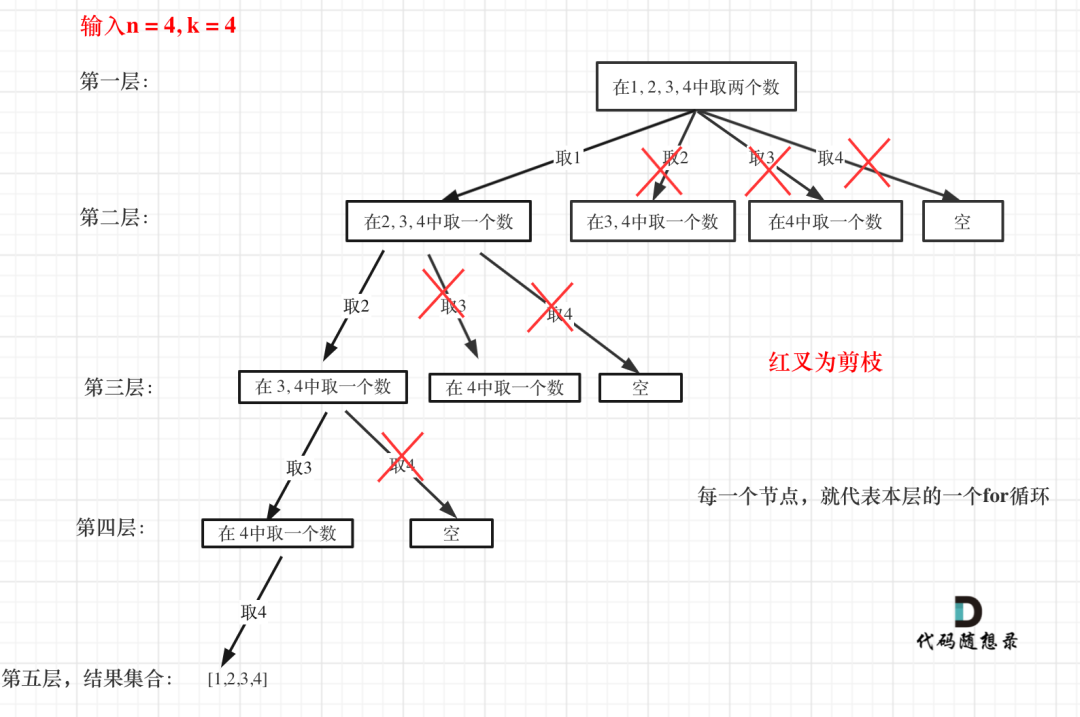
优化剪枝操作

剪枝操作是回溯算法的一种优化方法，可以排除不满足解的情况来提高算法的执行效率。在回溯算法中，剪枝操作可以有多种方式，例如对for循环选择的起始范围的剪枝，或者在递归过程中判断是否需要继续递归等等

import java.util.*;

public class Solution {

    // 回溯函数
    private void backtracking(List<List<Integer>> result, List<Integer> path, int n, int k, int startIndex) {
        if (path.size() == k) { // 如果path中的元素个数等于k，说明找到了一组符合条件的组合
            result.add(new ArrayList<>(path)); // 将该组合加入结果集中
            return; // 返回上一层递归
        }
        // 枚举所有可能的数
        for (int i = startIndex; i <=  n - (k - path.size()) + 1; i++) {//优化的地方
            path.add(i); // 将当前数加入path中，进行处理
            backtracking(result, path, n, k, i + 1); // 递归处理下一个数
            path.remove(path.size() - 1); // 撤销处理的数，回溯到上一层状态
        }
    }

    // 组合函数
    public List<List<Integer>> combine(int n, int k) {
        List<List<Integer>> result = new ArrayList<>(); // 存储符合条件的结果集
        List<Integer> path = new ArrayList<>(); // 存储符合条件的组合
        backtracking(result, path, n, k, 1); // 开始回溯，从数字1开始
        return result; // 返回结果集
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int n = scanner.nextInt(); // 获取用户输入的n
        int k = scanner.nextInt(); // 获取用户输入的k
        scanner.close(); // 关闭Scanner
        Solution solution = new Solution(); // 创建Solution对象
        List<List<Integer>> result = solution.combine(n, k); // 调用组合函数，得到符合条件的结果集
        for (List<Integer> list : result) { // 遍历结果集
            for (int num : list) { // 遍历组合
                System.out.print(num + " "); // 输出组合中的元素
            }
            System.out.println(); // 输出换行，用于分隔每个组合
        }
    }
}

2.2组合总和

找出所有相加之和为 n 的 k 个数的组合。组合中只允许含有 1 - 9 的正整数，并且每种组合中不存在重复的数字。

说明：

所有数字都是正整数。

解集不能包含重复的组合。

示例 1:
输入: k = 3, n = 7
输出: [[1,2,4]]

思路

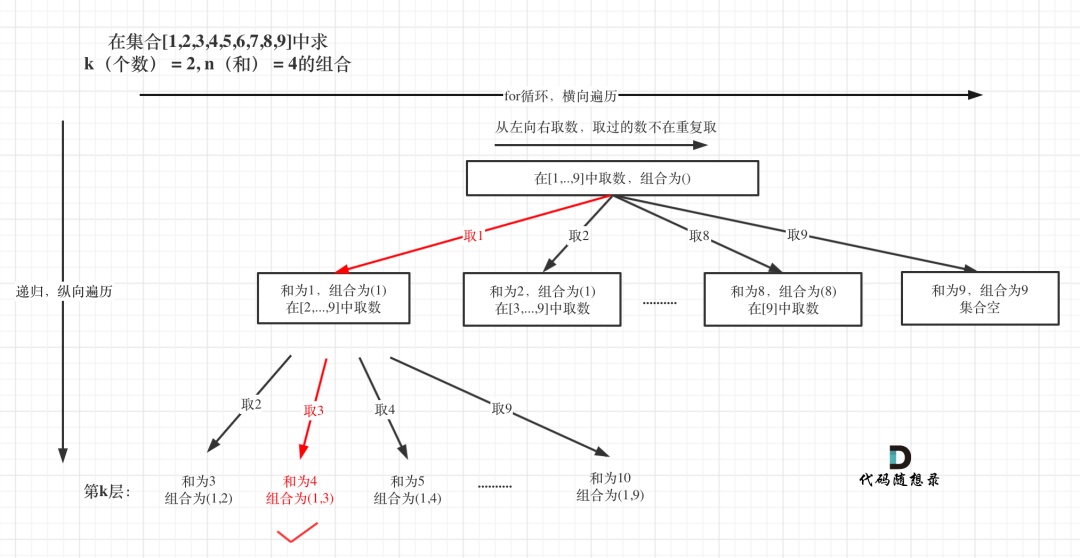
本题就是在[1,2,3,4,5,6,7,8,9]这个集合中找到和为n的k个数的组合。

相对于上题，无非就是多了一个限制，本题是要找到和为n的k个数的组合，而整个集合已经是固定的了[1,...,9]。

例如 k = 2，n = 4的话，就是在集合[1,2,3,4,5,6,7,8,9]中求 k（个数） = 2, n（和） = 4的组合。

import java.util.*;

class Solution {
    private List<List<Integer>> result; // 存放结果集
    private List<Integer> path; // 符合条件的结果

    /**
     * backtracking - 回溯算法
     *
     * @param targetSum   目标和，也就是题目中的n。
     * @param k           题目中要求k个数的集合。
     * @param sum         已经收集的元素的总和，也就是path里元素的总和。
     * @param startIndex 下一层for循环搜索的起始位置。
     */
    private void backtracking(int targetSum, int k, int sum, int startIndex) {
        // 剪枝操作：如果path里的元素个数已经等于k，且当前元素总和不等于目标和targetSum，直接返回。
        if (path.size() == k && sum != targetSum) {
            return;
        }
        // 如果path里的元素个数已经等于k，且当前元素总和等于目标和targetSum，说明已经找到了符合条件的结果，加入到结果集中并返回。
        if (path.size() == k && sum == targetSum) {
            result.add(new ArrayList<>(path));
            return;
        }
        for (int i = startIndex; i <= 9; i++) {
            sum += i; // 处理
            path.add(i); // 处理
            backtracking(targetSum, k, sum, i + 1); // 注意i+1调整startIndex
            sum -= i; // 回溯
            path.remove(path.size() - 1); // 回溯
        }
    }

    public List<List<Integer>> combinationSum3(int k, int n) {
        result = new ArrayList<>();
        path = new ArrayList<>();
        backtracking(n, k, 0, 1);
        return result;
    }

    public static void main(String[] args) {
        Scanner scanner = new Scanner(System.in);
        int k = scanner.nextInt(); // 读取sin
        int n = scanner.nextInt(); // 读取n
        Solution solution = new Solution();
        List<List<Integer>> result = solution.combinationSum3(k, n);
        System.out.println(result);
    }
}

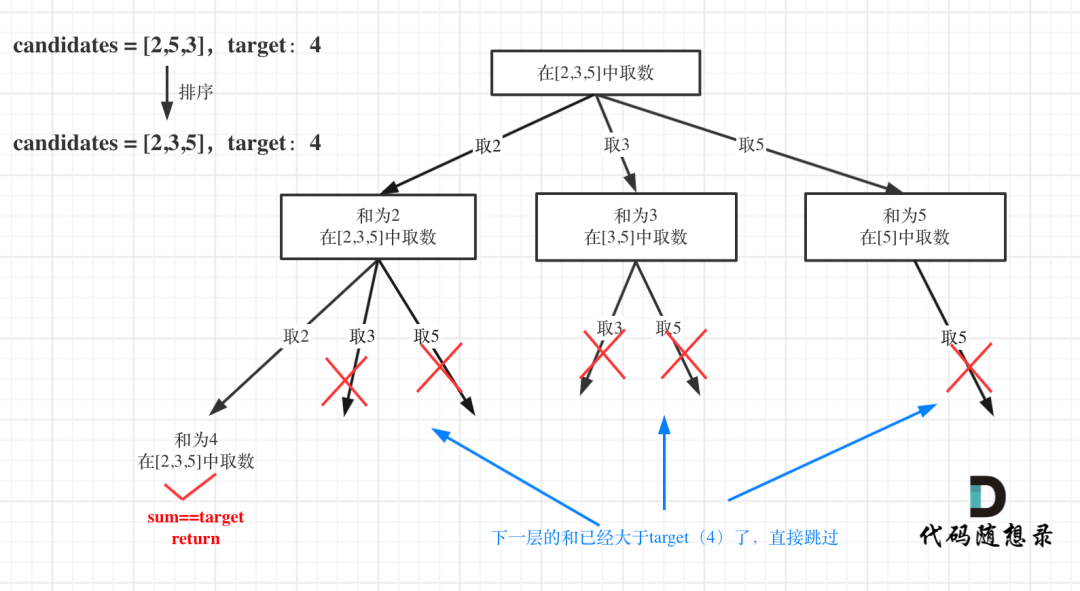
2.3组合总和2

给定一个无重复元素的数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的数字可以无限制重复被选取。

说明：

所有数字（包括 target）都是正整数。

解集不能包含重复的组合。

示例 1：输入：candidates = [2,3,6,7], target = 7, 所求解集为：[ [7], [2,2,3] ]

提示

组合没有数量要求

元素可无限重复选

import java.util.*;

class Solution {
    public List<List<Integer>> combinationSum(int[] candidates, int target) {
        List<List<Integer>> res = new ArrayList<>();
        Arrays.sort(candidates); // 先进行排序
        backtracking(res, new ArrayList<>(), candidates, target, 0, 0);
        return res;
    }

    public void backtracking(List<List<Integer>> res, List<Integer> path, int[] candidates, int target, int sum, int idx) {
        // 找到了数字和为 target 的组合
        if (sum == target) {
            res.add(new ArrayList<>(path));
            return;
        }

        for (int i = idx; i < candidates.length; i++) {
            // 如果 sum + candidates[i] > target 就终止遍历
            if (sum + candidates[i] > target) break;
            path.add(candidates[i]);
            backtracking(res, path, candidates, target, sum + candidates[i], i);
            path.remove(path.size() - 1); // 回溯，移除路径 path 最后一个元素
        }
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        int[] candidates1 = {2, 3, 6, 7};
        int target1 = 7;
        List<List<Integer>> res1 = s.combinationSum(candidates1, target1);
        System.out.println(res1); // [[7], [2, 2, 3]]

        int[] candidates2 = {2, 3, 5};
        int target2 = 8;
        List<List<Integer>> res2 = s.combinationSum(candidates2, target2);
        System.out.println(res2); // [[2, 2, 2, 2], [2, 3, 3], [3, 5]]
    }
}

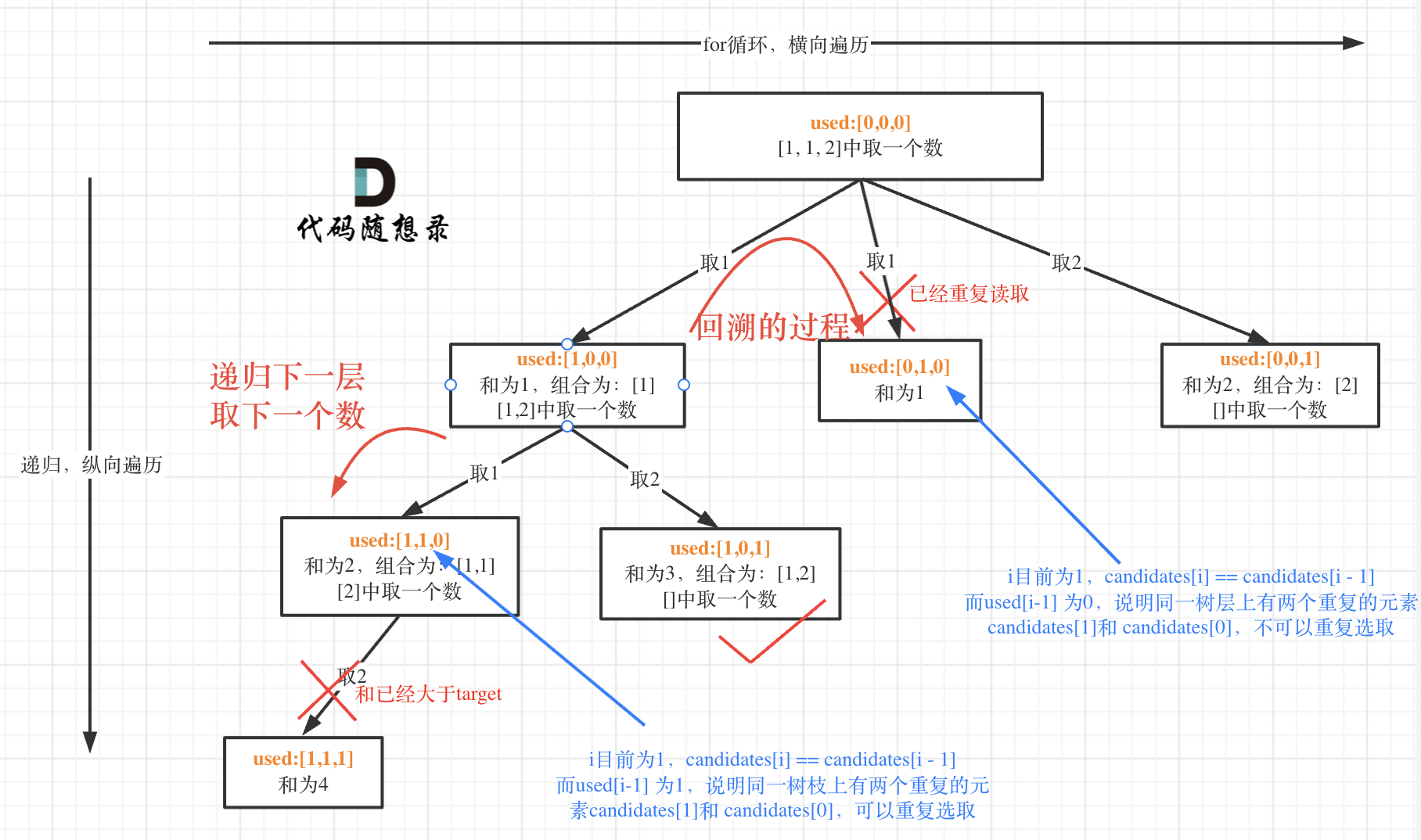
2.4组合总和3

给定一个数组 candidates 和一个目标数 target ，找出 candidates 中所有可以使数字和为 target 的组合。

candidates 中的每个数字在每个组合中只能使用一次。

说明：所有数字（包括目标数）都是正整数。解集不能包含重复的组合。
示例 1:
输入: candidates = [10,1,2,7,6,1,5], target = 8,
所求解集为:
[
  [1, 7],
  [1, 2, 5],
  [2, 6],
  [1, 1, 6]
]

思路

本题candidates 中的每个数字在每个组合中只能使用一次。
本题数组candidates的元素是有重复的

import java.util.*;

class Solution {
    LinkedList<Integer> path = new LinkedList<>();
    List<List<Integer>> ans = new ArrayList<>();
    boolean[] used;
    int sum = 0;

    public List<List<Integer>> combinationSum2(int[] candidates, int target) {
        used = new boolean[candidates.length];
        // 加标志数组，用来辅助判断同层节点是否已经遍历
        Arrays.fill(used, false);
        // 为了将重复的数字都放到一起，所以先进行排序
        Arrays.sort(candidates);
        backTracking(candidates, target, 0);
        return ans;
    }

    private void backTracking(int[] candidates, int target, int startIndex) {
        if (sum == target) {
            ans.add(new ArrayList(path));
        }
        for (int i = startIndex; i < candidates.length; i++) {
            if (sum + candidates[i] > target) {
                break;
            }
            // 出现重复节点，同层的第一个节点已经被访问过，所以直接跳过
            if (i > 0 && candidates[i] == candidates[i - 1] && !used[i - 1]) {
                continue;
            }
            used[i] = true;
            sum += candidates[i];
            path.add(candidates[i]);
            // 每个节点仅能选择一次，所以从下一位开始
            backTracking(candidates, target, i + 1);
            used[i] = false;
            sum -= candidates[i];
            path.removeLast();
        }
    }

    public static void main(String[] args) {
        Solution s = new Solution();
        int[] candidates = {10, 1, 2, 7, 6, 1, 5};
        int target = 8;
        List<List<Integer>> result = s.combinationSum2(candidates, target);
        System.out.println(result); // expected: [[1, 1, 6], [1, 2, 5], [1, 7], [2, 6]]
    }
}

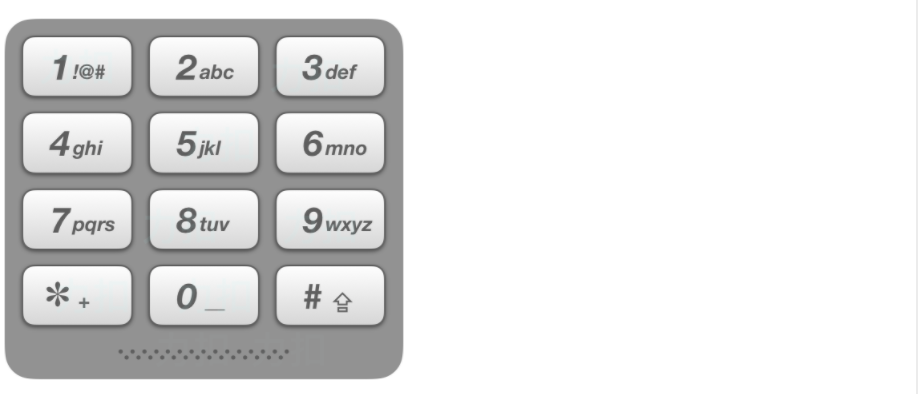
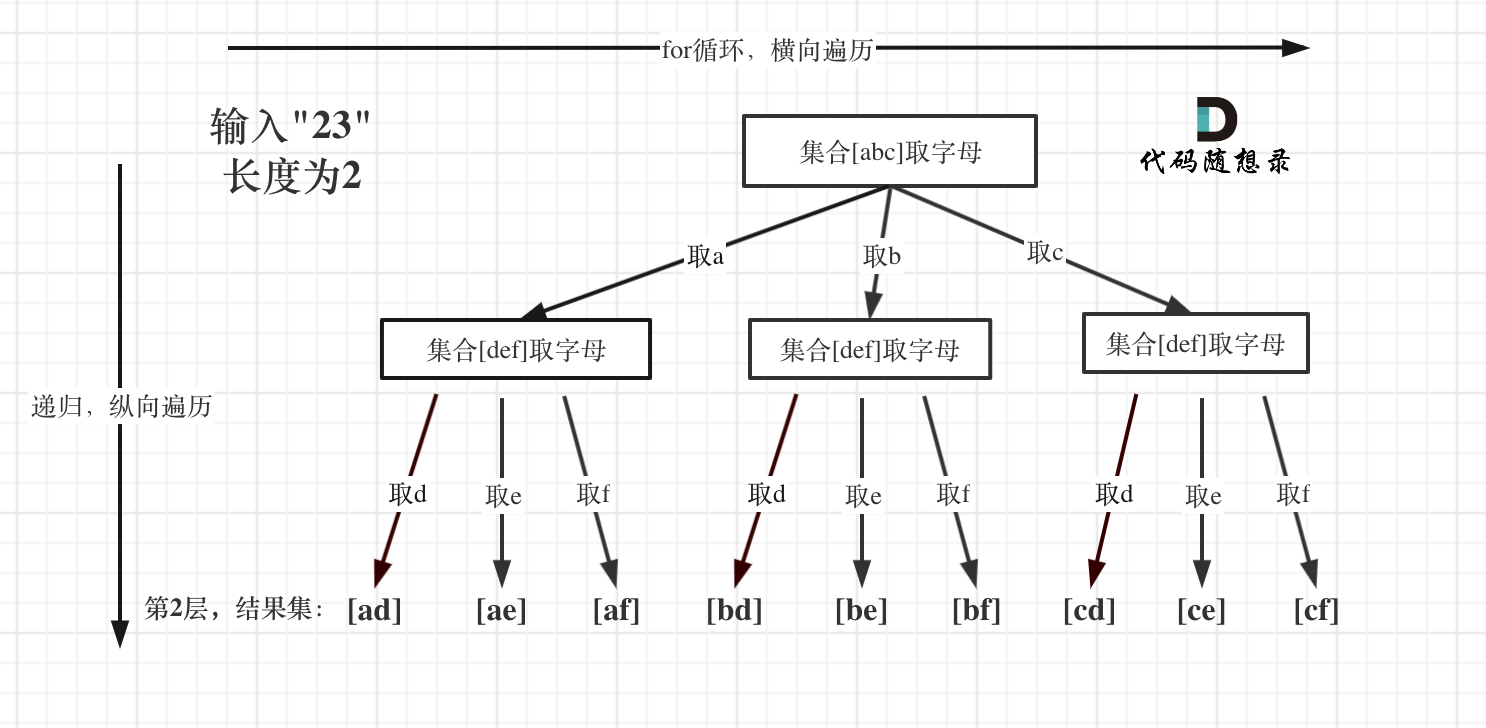
2.5电话号码的字母组合

给定一个仅包含数字 2-9 的字符串，返回所有它能表示的字母组合。

给出数字到字母的映射如下（与电话按键相同）。注意 1 不对应任何字母。

示例:

输入："23"
输出：["ad", "ae", "af", "bd", "be", "bf", "cd", "ce", "cf"].

说明：尽管上面的答案是按字典序排列的，但是你可以任意选择答案输出的顺序。

import java.util.*;

class Solution {
    // 字母映射表
    private final String[] letterMap = {
            "",     // 0
            "",     // 1
            "abc",  // 2
            "def",  // 3
            "ghi",  // 4
            "jkl",  // 5
            "mno",  // 6
            "pqrs", // 7
            "tuv",  // 8
            "wxyz"  // 9
    };

    private List<String> result = new ArrayList<>(); // 存储所有结果
    private StringBuilder s = new StringBuilder(); // 存储每个组合

    private void backtracking(String digits, int index) {
        if (index == digits.length()) { // 当处理到最后一个数字时，将s加入result中
            result.add(s.toString());
            return;
        }
        int digit = digits.charAt(index) - '0'; // 将当前数字转为int
        String letters = letterMap[digit]; // 找出数字对应的字符集
        for (int i = 0; i < letters.length(); i++) {
            s.append(letters.charAt(i)); // 将当前字符加入s
            backtracking(digits, index + 1); // 递归到下一个数字
            s.deleteCharAt(s.length() - 1); // 回溯，将最后一个字符删除
        }
    }

    public List<String> letterCombinations(String digits) {
        result.clear(); // 清空result
        s.setLength(0); // 清空s
        if (digits.length() == 0) { // 边界条件，当输入为空时，直接返回result
            return result;
        }
        backtracking(digits, 0); // 从第一个数字开始处理
        return result;
    }
    
}
    public class Main {
    public static void main(String[] args) {
        Solution sol = new Solution();
        String digits1 = "23";
        List<String> res1 = sol.letterCombinations(digits1);
        System.out.println(res1);

        String digits2 = "";
        List<String> res2 = sol.letterCombinations(digits2);
        System.out.println(res2);

        String digits3 = "2";
        List<String> res3 = sol.letterCombinations(digits3);
        System.out.println(res3);
    }
}

三、切割问题

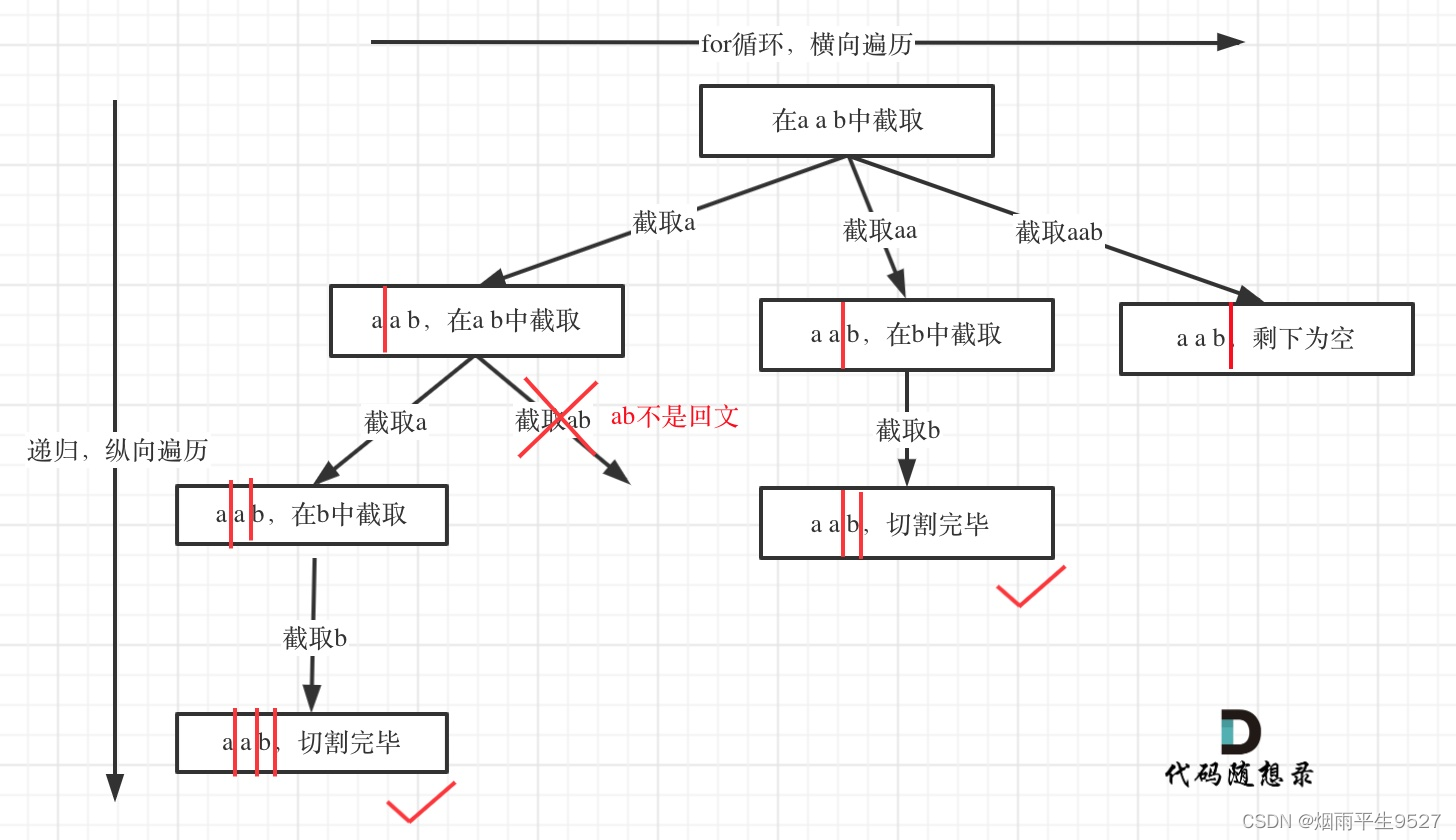
3.1分割回文串

给定一个字符串 s，将 s 分割成一些子串，使每个子串都是回文串。

返回 s 所有可能的分割方案。

示例: 输入: "aab" 输出: [ ["aa","b"], ["a","a","b"] ]

思路

切割问题，有不同的切割方式
判断回文

import java.util.*;

class Solution {
    private List<List<String>> result = new ArrayList<>();
    private List<String> path = new ArrayList<>(); // 存放已经回文的子串

    private void backtracking(String s, int startIndex) {
        // 如果起始位置已经大于s的大小，说明已经找到了一组分割方案了
        if (startIndex >= s.length()) {
            result.add(new ArrayList<>(path));
            return;
        }

        for (int i = startIndex; i < s.length(); i++) {
            if (isPalindrome(s, startIndex, i)) {   // 是回文子串
                // 获取[startIndex,i]在s中的子串
                String str = s.substring(startIndex, i + 1);
                path.add(str);
            } else {                                // 不是回文，跳过
                continue;
            }
            backtracking(s, i + 1); // 寻找i+1为起始位置的子串
            path.remove(path.size() - 1); // 回溯过程，弹出本次已经填在的子串
        }
    }

    private boolean isPalindrome(String s, int start, int end) {
        // 判断从start到end的子串是否是回文子串
        while (start < end) {
            if (s.charAt(start++) != s.charAt(end--)) {
                return false;
            }
        }
        return true;
    }

    public List<List<String>> partition(String s) {
        result.clear();
        path.clear();
        backtracking(s, 0);
        return result;
    }
}
public class Main {
    public static void main(String[] args) {
        Solution sol = new Solution();

        List<List<String>> res1 = sol.partition("aab");
        System.out.println(res1);

        List<List<String>> res2 = sol.partition("a");
        System.out.println(res2);

        List<List<String>> res3 = sol.partition("racecar");
        System.out.println(res3);
    }
}

3.2.复原IP地址

给定一个只包含数字的字符串，复原它并返回所有可能的 IP 地址格式。

有效的 IP 地址正好由四个整数（每个整数位于 0 到 255 之间组成，且不能含有前导 0），整数之间用 '.' 分隔。

例如："0.1.2.201" 和 "192.168.1.1" 是有效的 IP 地址，但是 "0.011.255.245"、"192.168.1.312" 和 "192.168@1.1" 是无效的 IP 地址。

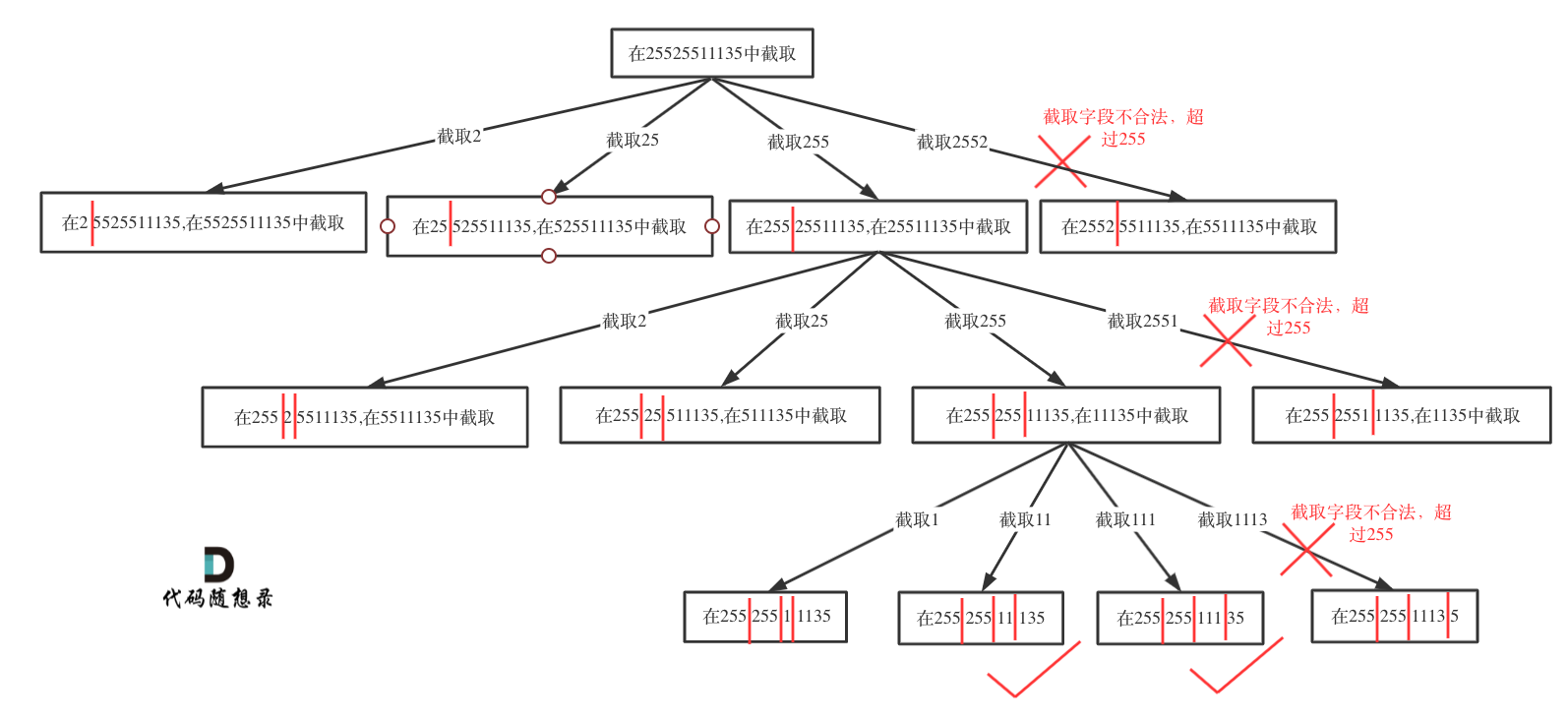
示例 1：

输入：s = "25525511135"
输出：["255.255.11.135","255.255.111.35"]

示例 2：

输入：s = "0000"
输出：["0.0.0.0"]

提示

切割问题就可以使用回溯搜索法把所有可能性搜出来

import java.util.*;

class Solution {
    private List<String> result = new ArrayList<>(); // 记录结果

    // startIndex: 搜索的起始位置，pointNum:添加逗点的数量
    private void backtracking(String s, int startIndex, int pointNum) {
        if (pointNum == 3) { // 逗点数量为3时，分隔结束
            // 判断第四段子字符串是否合法，如果合法就放进result中
            if (isValid(s, startIndex, s.length() - 1)) {
                result.add(s);
            }
            return;
        }
        for (int i = startIndex; i < s.length(); i++) {
            if (isValid(s, startIndex, i)) { // 判断 [startIndex,i] 这个区间的子串是否合法
                s = s.substring(0, i + 1) + "." + s.substring(i + 1); // 在i的后面插入一个逗点
                pointNum++;
                backtracking(s, i + 2, pointNum); // 插入逗点之后下一个子串的起始位置为i+2
                pointNum--; // 回溯
                s = s.substring(0, i + 1) + s.substring(i + 2); // 回溯删掉逗点
            } else {
                break; // 不合法，直接结束本层循环
            }
        }
    }

    // 判断字符串s在左闭右闭区间[start, end]所组成的数字是否合法
    private boolean isValid(String s, int start, int end) {
        if (start > end) {
            return false;
        }
        if (s.charAt(start) == '0' && start != end) { // 0开头的数字不合法
            return false;
        }
        int num = 0;
        for (int i = start; i <= end; i++) {
            if (s.charAt(i) > '9' || s.charAt(i) < '0') { // 遇到非数字字符不合法
                return false;
            }
            num = num * 10 + (s.charAt(i) - '0');
            if (num > 255) { // 如果大于255了不合法
                return false;
            }
        }
        return true;
    }

    public List<String> restoreIpAddresses(String s) {
        result.clear();
        if (s.length() < 4 || s.length() > 12) {
            return result; // 算是剪枝了
        }
        backtracking(s, 0, 0);
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        List<String> result = solution.restoreIpAddresses("25525511135");
        System.out.println(result); // ["255.255.11.135", "255.255.111.35"]
    }
}

四、子集问题

4.1子集

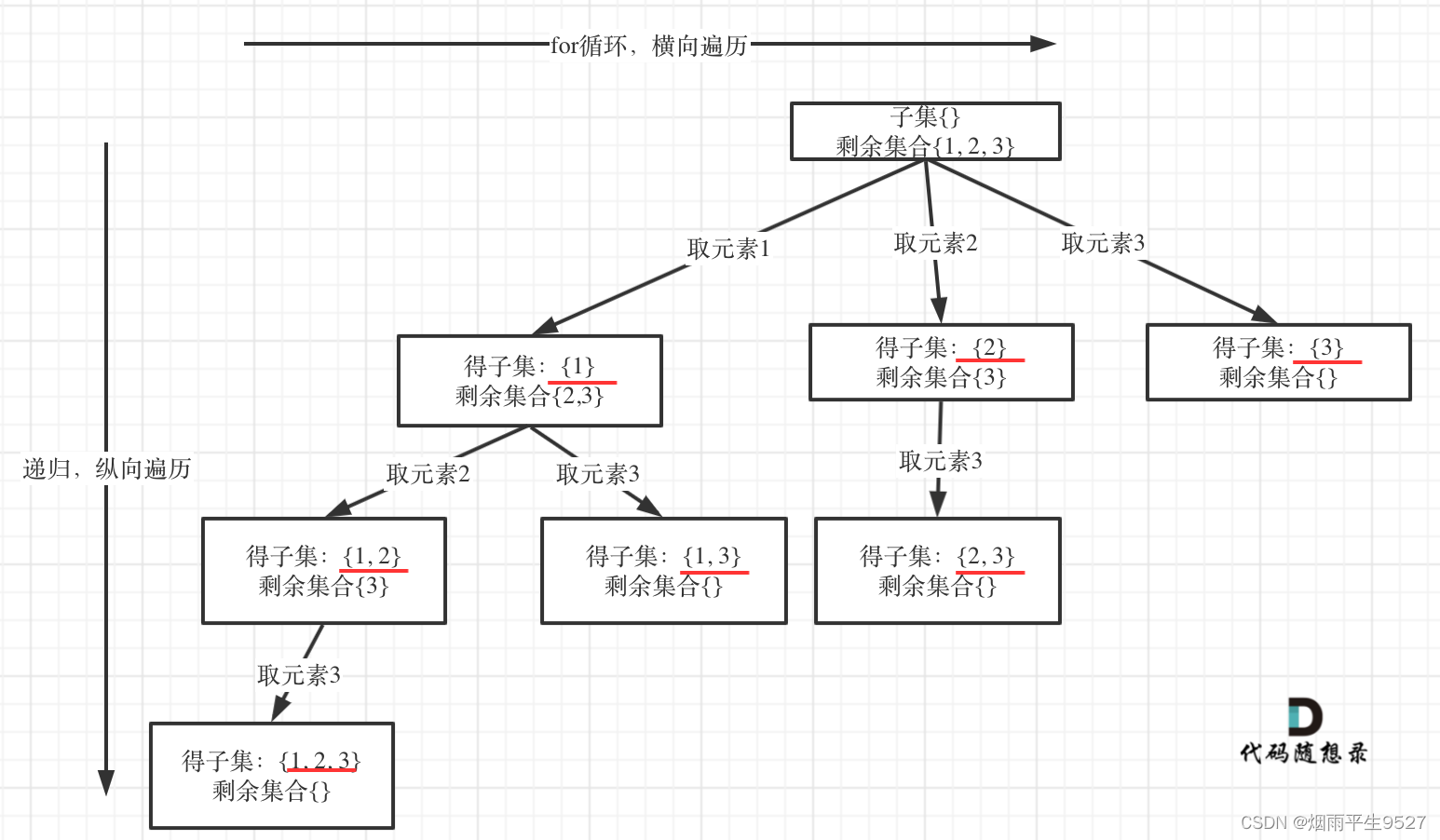
给定一组不含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例: 输入: nums = [1,2,3] 输出: [ [3], [1], [2], [1,2,3], [1,3], [2,3], [1,2], [] ]

import java.util.ArrayList;
import java.util.List;

class Solution {
    List<List<Integer>> result = new ArrayList<>(); // 存储所有的子集
    List<Integer> path = new ArrayList<>(); // 存储当前正在生成的子集

    public List<List<Integer>> subsets(int[] nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }

    private void backtracking(int[] nums, int startIndex) {
        result.add(new ArrayList<>(path)); // 加入当前生成的子集
        if (startIndex == nums.length) { // 终止条件
            return;
        }
        for (int i = startIndex; i < nums.length; i++) {
            path.add(nums[i]);
            backtracking(nums, i + 1); // 从i+1开始搜索，避免重复
            path.remove(path.size() - 1); // 回溯
        }
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] nums = {1, 2, 3};
        List<List<Integer>> subsets = solution.subsets(nums);
        for (List<Integer> subset : subsets) {
            System.out.println(subset);
        }
    }
}

4.2子集2

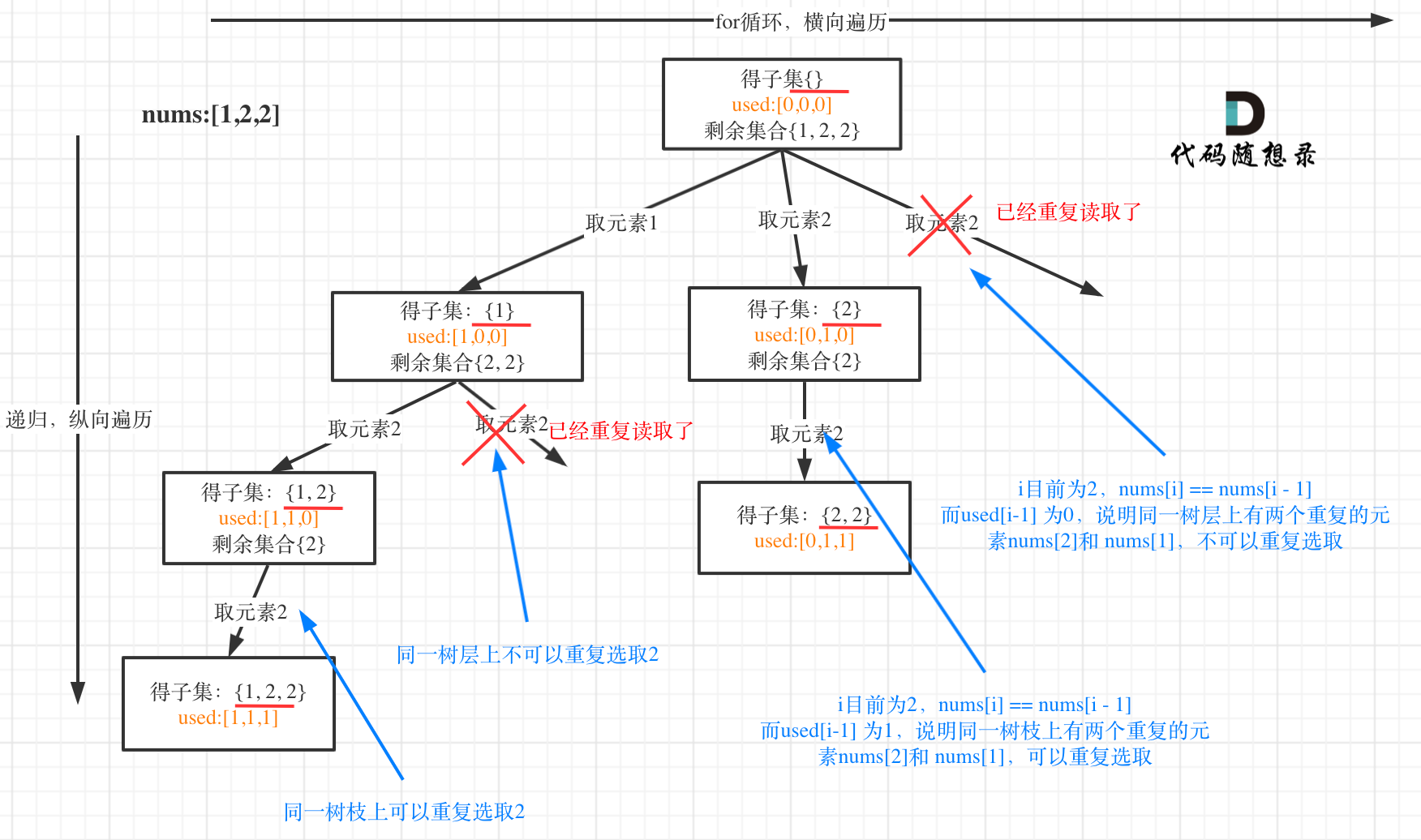
给定一个可能包含重复元素的整数数组 nums，返回该数组所有可能的子集（幂集）。

说明：解集不能包含重复的子集。

示例:

输入: [1,2,2]
输出: [ [2], [1], [1,2,2], [2,2], [1,2], [] ]

思路

集合里有重复元素了，而且求取的子集要去重。

import java.util.*;

class Solution {
    private List<List<Integer>> result;
    private List<Integer> path;

    private void backtracking(int[] nums, int startIndex) {
        result.add(new ArrayList<>(path)); // 收集子集
        for (int i = startIndex; i < nums.length; i++) {
            // 如果这个元素和上一个元素一样，并且上一个元素没有被选中，那么这个元素也不用选
            if (i > startIndex && nums[i] == nums[i - 1]) {
                continue;
            }
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }

    public List<List<Integer>> subsetsWithDup(int[] nums) {
        result = new ArrayList<>();
        path = new ArrayList<>();
        Arrays.sort(nums); // 数组排序
        backtracking(nums, 0);
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] nums = {1, 2, 2};
        List<List<Integer>> subsets = solution.subsetsWithDup(nums);
        for (List<Integer> subset : subsets) {
            System.out.println(subset.toString());
        }
    }
}

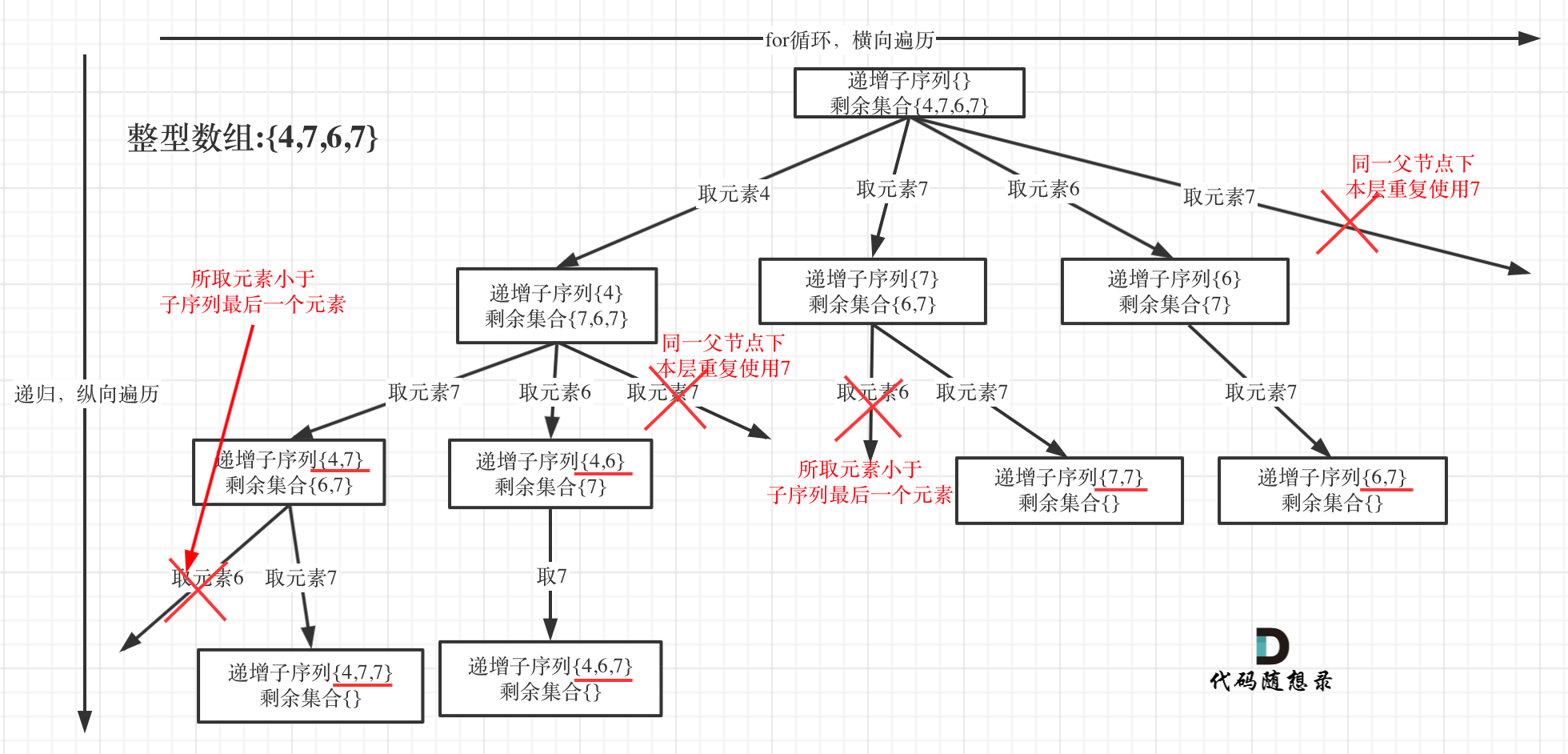
4.3递增子序列

给定一个整型数组, 你的任务是找到所有该数组的递增子序列，递增子序列的长度至少是2。

示例:

输入: [4, 6, 7, 7]
输出: [[4, 6], [4, 7], [4, 6, 7], [4, 6, 7, 7], [6, 7], [6, 7, 7], [7,7], [4,7,7]]

说明:

给定数组的长度不会超过15。
数组中的整数范围是 [-100,100]。
给定数组中可能包含重复数字，相等的数字应该被视为递增的一种情况。

import java.util.*;

class Solution {
    private List<List<Integer>> result = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    private void backtracking(int[] nums, int startIndex) {
        if (path.size() > 1) {
            result.add(new ArrayList<>(path)); // 注意这里要new一个新的list
            // 注意这里不要加return，要取树上的节点
        }
        Set<Integer> set = new HashSet<>(); // 使用set对本层元素进行去重
        for (int i = startIndex; i < nums.length; i++) {
            if ((!path.isEmpty() && nums[i] < path.get(path.size() - 1))
                    || set.contains(nums[i])) {
                continue;
            }
            set.add(nums[i]); // 记录这个元素在本层用过了，本层后面不能再用了
            path.add(nums[i]);
            backtracking(nums, i + 1);
            path.remove(path.size() - 1);
        }
    }

    public List<List<Integer>> findSubsequences(int[] nums) {
        result.clear();
        path.clear();
        backtracking(nums, 0);
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] nums = {4, 6, 7, 7};
        List<List<Integer>> result = solution.findSubsequences(nums);
        System.out.println(result);
    }
}

五、排列问题

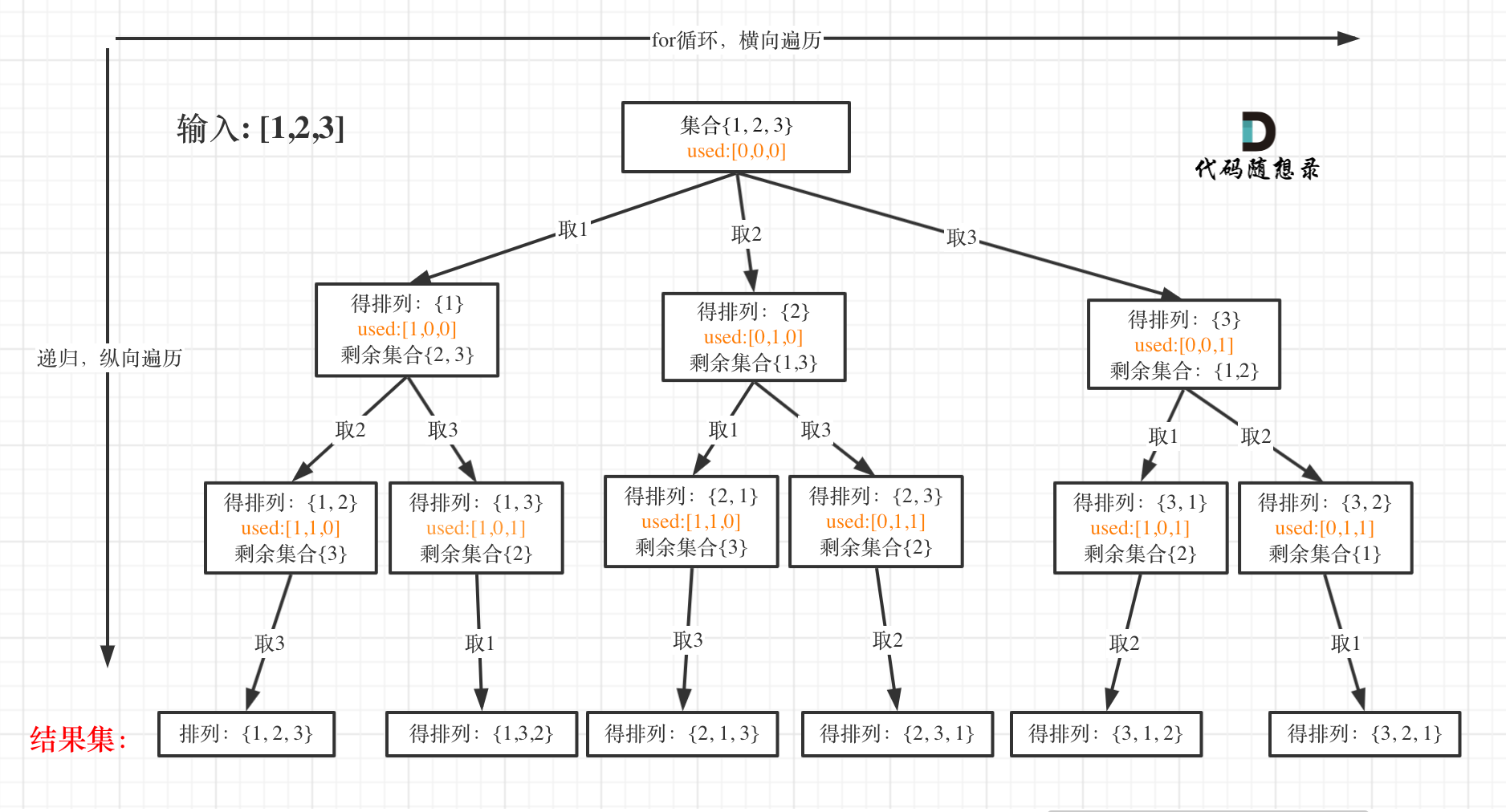
5.1全排列

给定一个没有重复数字的序列，返回其所有可能的全排列。

示例:

输入: [1,2,3]
输出: [ [1,2,3], [1,3,2], [2,1,3], [2,3,1], [3,1,2], [3,2,1] ]

import java.util.*;

class Solution {
    public List<List<Integer>> result = new ArrayList<>();
    public List<Integer> path = new ArrayList<>();

    // 回溯算法
    public void backtracking(List<Integer> nums, boolean[] used) {
        // 如果当前path中的数字数量等于nums中的数字数量，则已经找到一组答案
        if (path.size() == nums.size()) {
            result.add(new ArrayList<>(path));
            return;
        }

        // 枚举nums中所有的数字
        for (int i = 0; i < nums.size(); i++) {
            // 如果当前数字已经使用过，则跳过
            if (used[i]) {
                continue;
            }

            // 标记当前数字已经使用过
            used[i] = true;
            // 将当前数字加入到path中
            path.add(nums.get(i));
            // 继续递归查找
            backtracking(nums, used);
            // 回溯
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }

    public List<List<Integer>> permute(List<Integer> nums) {
        result.clear();
        path.clear();
        boolean[] used = new boolean[nums.size()];
        backtracking(nums, used);
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        List<Integer> nums = new ArrayList<>(Arrays.asList(1, 2, 3));
        List<List<Integer>> result = solution.permute(nums);
        System.out.println(result);
    }
}

asList是Java中的一个方法，它可以将数组转换为List。返回的List是由指定数组支持的固定大小的列表。该方法可以作为基于数组和基于集合的API之间的桥梁

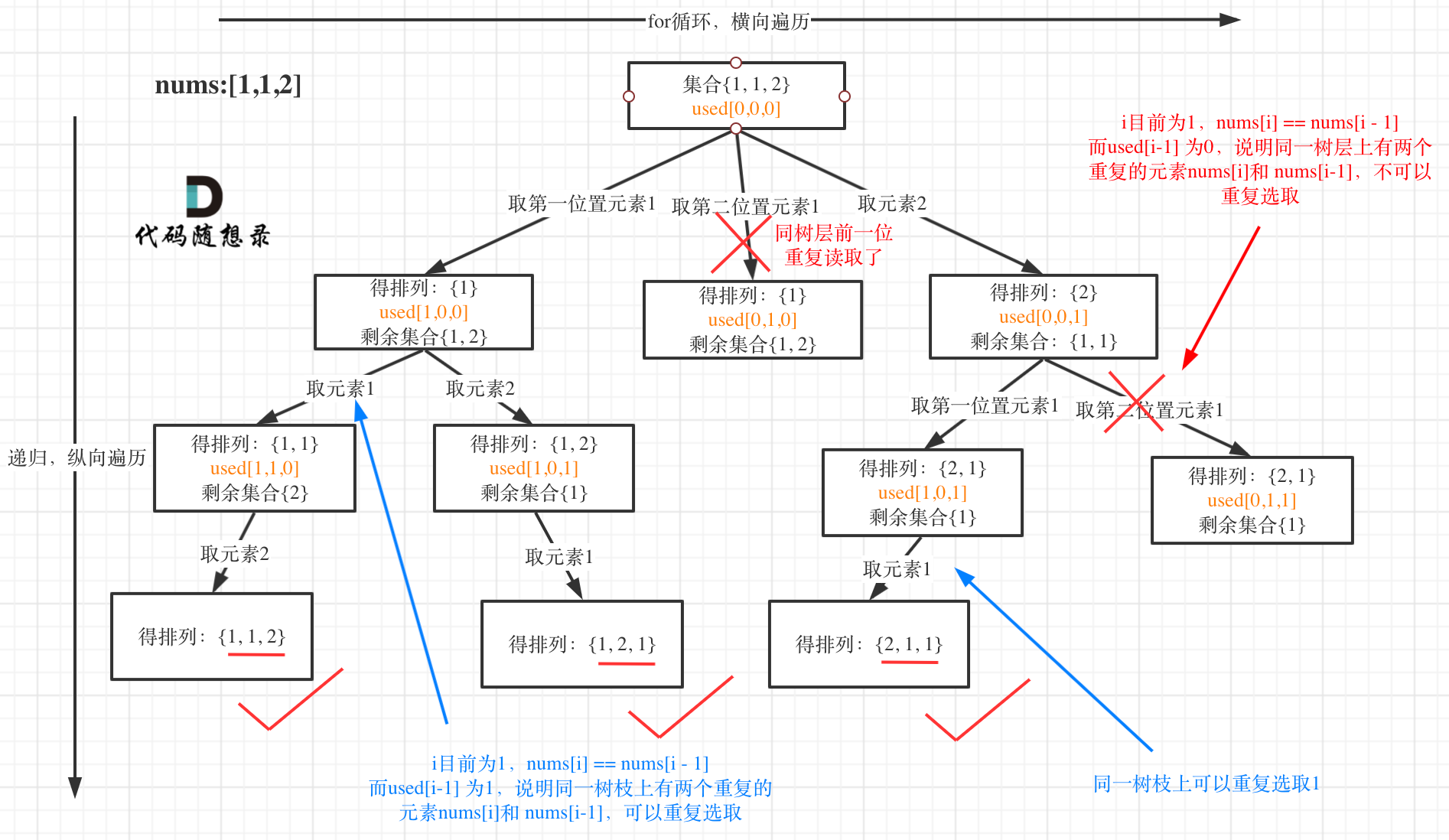
5.2全排列 II

给定一个可包含重复数字的序列 nums ，按任意顺序返回所有不重复的全排列。

示例 1：

输入：nums = [1,1,2]
输出： [[1,1,2], [1,2,1], [2,1,1]]

import java.util.*;

class Solution {
    private List<List<Integer>> result = new ArrayList<>();
    private List<Integer> path = new ArrayList<>();

    private void backtracking(int[] nums, boolean[] used) {
        // 如果当前组合中的数字数量等于数组的长度，说明找到了一组，加入结果集中
        if (path.size() == nums.length) {
            result.add(new ArrayList<>(path)); // 注意需要新建一个ArrayList，否则结果会受到后续操作的影响
            return;
        }

        for (int i = 0; i < nums.length; i++) {
            // 如果当前数字已经被使用过，跳过
            if (used[i]) {
                continue;
            }
            // 如果当前数字和前一个数字相同，并且前一个数字没有被使用过，则跳过
            if (i > 0 && nums[i] == nums[i-1] && !used[i-1]) {
                continue;
            }

            // 将当前数字加入组合中
            path.add(nums[i]);
            used[i] = true; // 标记当前数字已经被使用过

            // 继续搜索
            backtracking(nums, used);

            // 回溯，将当前数字从组合中删除，并标记为未使用过
            path.remove(path.size() - 1);
            used[i] = false;
        }
    }

    public List<List<Integer>> permuteUnique(int[] nums) {
        result.clear(); // 清空结果集
        path.clear(); // 清空当前组合
        Arrays.sort(nums); // 对数组进行排序，方便判断重复数字
        boolean[] used = new boolean[nums.length]; // 标记每个数字是否被使用过
        backtracking(nums, used); // 开始搜索
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int[] nums = {1, 1, 2};
        List<List<Integer>> result = solution.permuteUnique(nums);
        System.out.println(result);
    }
}

六、棋盘问题

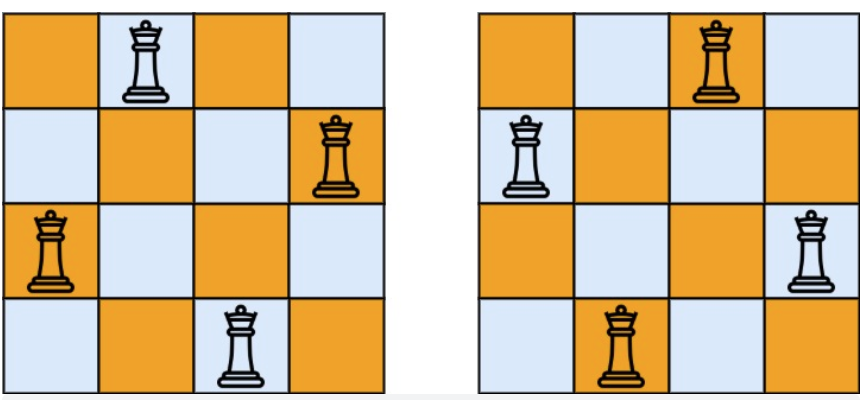
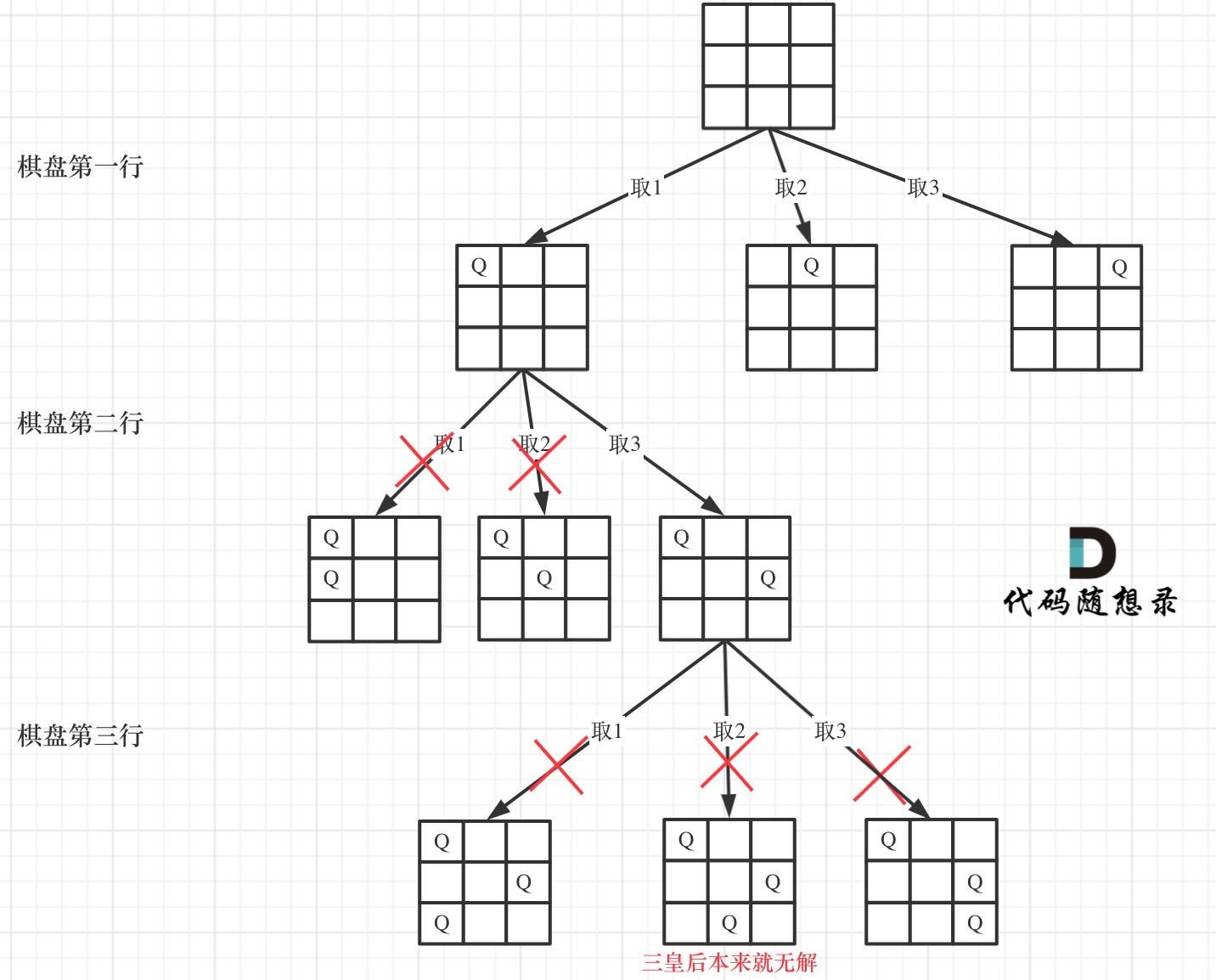
6.1N皇后

n 皇后问题研究的是如何将 n 个皇后放置在 n×n 的棋盘上，并且使皇后彼此之间不能相互攻击。

给你一个整数 n ，返回所有不同的 n 皇后问题的解决方案。

每一种解法包含一个不同的 n 皇后问题的棋子放置方案，该方案中 'Q' 和 '.' 分别代表了皇后和空位。

示例 1：

输入：n = 4
输出：[[".Q..","...Q","Q...","..Q."],["..Q.","Q...","...Q",".Q.."]]
解释：如上图所示，4 皇后问题存在两个不同的解法。

提示

首先来看一下皇后们的约束条件：

不能同行
不能同列
不能同斜线

import java.util.ArrayList;
import java.util.List;

class Solution {
    private List<List<String>> result = new ArrayList<>();
    // n 为输入的棋盘大小
    // row 是当前递归到棋盘的第几行了
    private void backtracking(int n, int row, char[][] chessboard) {
        if (row == n) {
            result.add(charToStringList(chessboard));
            return;
        }
        for (int col = 0; col < n; col++) {
            if (isValid(row, col, chessboard, n)) { // 验证合法就可以放
                chessboard[row][col] = 'Q'; // 放置皇后
                backtracking(n, row + 1, chessboard);
                chessboard[row][col] = '.'; // 回溯，撤销皇后
            }
        }
    }

    private boolean isValid(int row, int col, char[][] chessboard, int n) {
        // 检查列
        for (int i = 0; i < row; i++) { // 这是一个剪枝
            if (chessboard[i][col] == 'Q') {
                return false;
            }
        }
        // 检查 45度角是否有皇后
        for (int i = row - 1, j = col - 1; i >=0 && j >= 0; i--, j--) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        // 检查 135度角是否有皇后
        for(int i = row - 1, j = col + 1; i >= 0 && j < n; i--, j++) {
            if (chessboard[i][j] == 'Q') {
                return false;
            }
        }
        return true;
    }

    private List<String> charToStringList(char[][] chessboard) {
        List<String> board = new ArrayList<>();
        for (char[] row : chessboard) {
            board.add(new String(row));
        }
        return board;
    }

    public List<List<String>> solveNQueens(int n) {
        result.clear();
        char[][] chessboard = new char[n][n];
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < n; j++) {
                chessboard[i][j] = '.';
            }
        }
        backtracking(n, 0, chessboard);
        return result;
    }

    public static void main(String[] args) {
        Solution solution = new Solution();
        int n = 4;
        List<List<String>> result = solution.solveNQueens(n);
        for (List<String> board : result) {
            for (String row : board) {
                System.out.println(row);
            }
            System.out.println();
        }
    }
}

6.2解数独

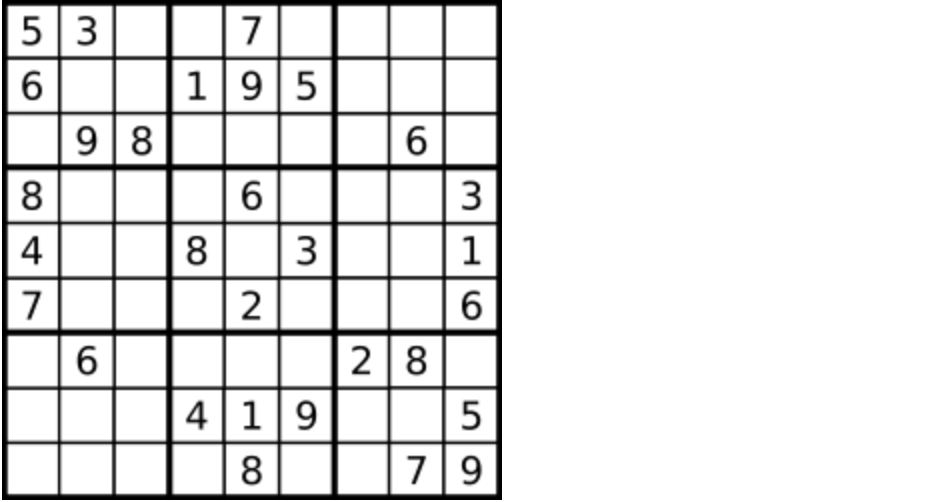
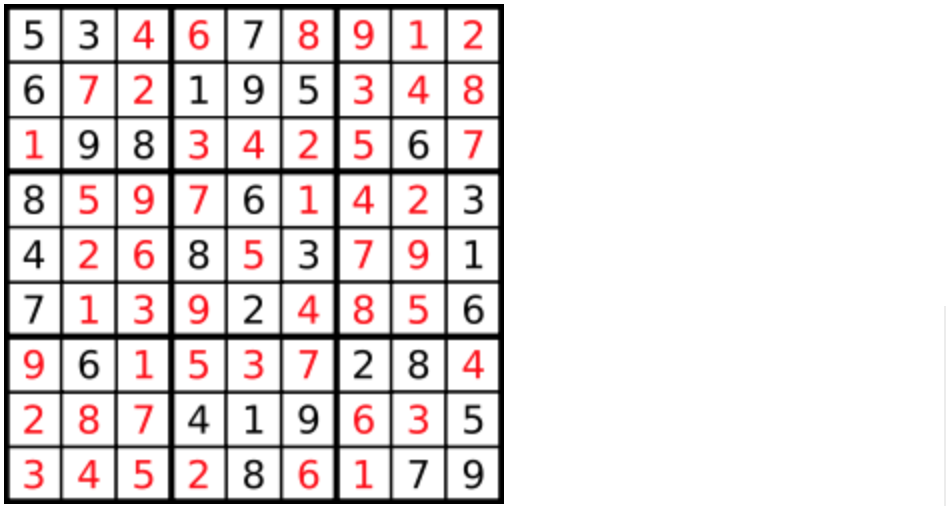
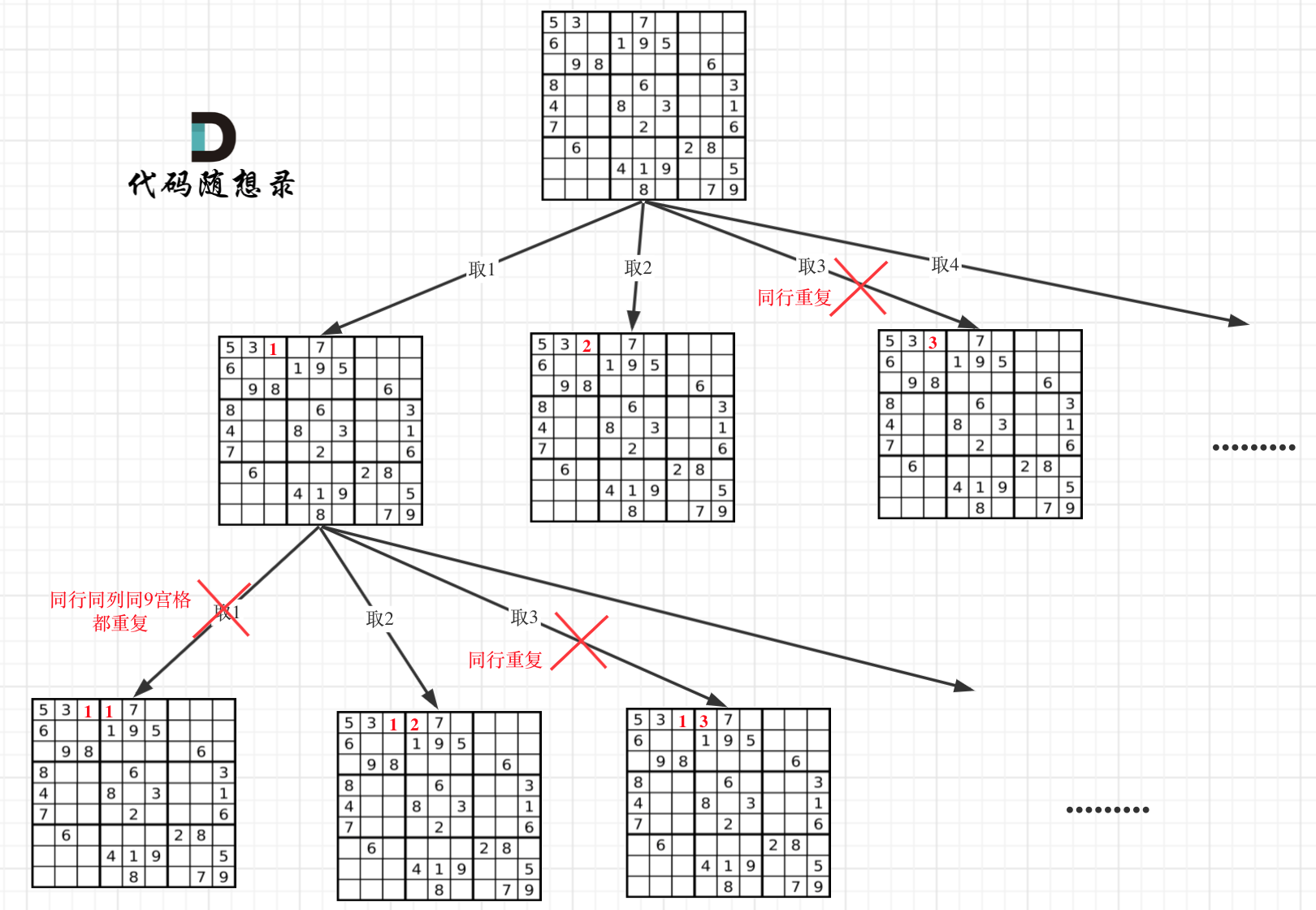
编写一个程序，通过填充空格来解决数独问题。

一个数独的解法需遵循如下规则：数字 1-9 在每一行只能出现一次。数字 1-9 在每一列只能出现一次。数字 1-9 在每一个以粗实线分隔的 3x3 宫内只能出现一次。空白格用 '.' 表示。

一个数独。

答案被标成红色。

提示：

给定的数独序列只包含数字 1-9 和字符 '.' 。
你可以假设给定的数独只有唯一解。
给定数独永远是 9x9 形式的。

import java.util.*;

class Solution {
    private boolean backtracking(char[][] board) {
        for (int i = 0; i < board.length; i++) { // 遍历行
            for (int j = 0; j < board[0].length; j++) { // 遍历列
                if (board[i][j] == '.') {
                    for (char k = '1'; k <= '9'; k++) { // (i, j) 这个位置放k是否合适
                        if (isValid(i, j, k, board)) {
                            board[i][j] = k; // 放置k
                            if (backtracking(board)) {
                                return true; // 如果找到合适一组立刻返回
                            }
                            board[i][j] = '.'; // 回溯，撤销k
                        }
                    }
                    return false; // 9个数都试完了，都不行，那么就返回false
                }
            }
        }
        return true; // 遍历完没有返回false，说明找到了合适棋盘位置了
    }

    private boolean isValid(int row, int col, char val, char[][] board) {
        for (int i = 0; i < 9; i++) { // 判断行里是否重复
            if (board[row][i] == val) {
                return false;
            }
        }
        for (int j = 0; j < 9; j++) { // 判断列里是否重复
            if (board[j][col] == val) {
                return false;
            }
        }
        int startRow = (row / 3) * 3;
        int startCol = (col / 3) * 3;
        for (int i = startRow; i < startRow + 3; i++) { // 判断9方格里是否重复
            for (int j = startCol; j < startCol + 3; j++) {
                if (board[i][j] == val) {
                    return false;
                }
            }
        }
        return true;
    }

    public void solveSudoku(char[][] board) {
        backtracking(board);
    }

    public static void main(String[] args) {
        Solution sol = new Solution();
        char[][] board = new char[][]{
                {'5','3','.','.','7','.','.','.','.'},
                {'6','.','.','1','9','5','.','.','.'},
                {'.','9','8','.','.','.','.','6','.'},
                {'8','.','.','.','6','.','.','.','3'},
                {'4','.','.','8','.','3','.','.','1'},
                {'7','.','.','.','2','.','.','.','6'},
                {'.','6','.','.','.','.','2','8','.'},
                {'.','.','.','4','1','9','.','.','5'},
                {'.','.','.','.','8','.','.','7','9'}
        };
        sol.solveSudoku(board);
        for (int i = 0; i < 9; i++) {
            System.out.println(Arrays.toString(board[i]));
        }
    }
}