Consistency Models- 理解
- 问题定义
- 研究动机
- 本文中心论点
- 相关工作和进展
- Consistency Models创新点
- review扩散模型
- Consistency Model-Definition
- 一致性模型的定义
- 一致性模型参数化
- 一致性模型采样
- Training Consistency Models via Distillation
- Training Consistency Models in Isolation

pdf:https://arxiv.org/pdf/2303.01469.pdf
github:https://github.com/openai/consistency_models
问题定义
图像编辑等
研究动机
扩散模型依赖于迭代生成过程,导致采样速度较慢,实时应用有限。
本文中心论点
- 给定一个概率流(PF) ODE,它能平滑地将数据转换为噪声。作者学习将ODE轨迹上的任何点(例如, x t , x t ′ x_t, x'_t xt,xt′)映射到它的原点(例如, x 0 x_0 x0),用于生成建模。
- 这些映射的模型称为一致性模型,因为对于同一轨迹上的点,他们的输出被训练为的一致的。
相关工作和进展
扩散模型受限于时间。
Consistency Models创新点
- 一致性模型在设计上支持快速的一步生成,同时仍然允许少步采样以换取样本质量的计算。
- 一种新的生成模型家族,可以在没有对抗性训练的情况下实现高样本质量
- 支持zero-shot数据编辑,如图像修补、着色和超分辨率,而不需要对这些任务进行明确的训练。
- 一致性模型既可以作为提取预训练扩散模型的一种方式训练,也可以作为独立的生成模型训练。
review扩散模型
将扩散理解为一个在时间上连续的变换过程(引入SDE形式来描述扩散模型的本质好处是“将理论分析和代码实现分离开来”,借助连续性SDE的数学工具做分析,实践的时候,则只需要用任意适当的离散化方案对SDE进行数值计算)
用随机微分方程(Stochastic Differential Equation,SDE)来描述扩散模型:

可以理解为下式(离散化):
![]()
在以前的论文中推导出上述SDE存在一个ODE形式的解轨迹(Probability Flow ODE)

![]()
SDE设计为让
p
T
(
x
)
p_T(x)
pT(x) 接近于易处理的高斯分布。采用别人论文中的设置,带入到(2)中
![]()
首先训练一个得分模型
s
ϕ
(
x
,
t
)
≈
▽
l
o
g
p
t
(
x
)
s_\phi (\mathbf{x},t) \approx\bigtriangledown logp_t(\mathbf{x})
sϕ(x,t)≈▽logpt(x),(2)转化为。称为empirical PF ODE

采样
x
^
∼
π
=
N
(
0
,
T
2
I
)
\widehat{\mathbf{x}} \sim \pi = N (0,T^2 I)
x
∼π=N(0,T2I)来初始化empirical PF ODE
- 利用现有的数值ODE solver来求解(Euler,Heun solvers等)
- 得到的 x ^ \widehat{\mathbf{x}} x 可以被看作是数据分布 p d a t a ( x ) p_{data}(\mathbf{x}) pdata(x)的一个近似样本。
- 考虑到数值稳定性,往往不会直接求出原图,而是取一个很小的值逐步来进行近似,并持续这个过程来求出。(导致速度慢)
Consistency Model-Definition
一致性模型的定义
假设存在一个函数f,对于同一条PF ODE轨迹上的任意点都有相同的输出
f
(
x
t
,
t
)
=
f
(
x
t
′
,
t
′
)
for all
t
,
t
′
∈
[
ϵ
,
T
]
\boldsymbol{f}\left(\mathrm{x}_{t}, t\right)=\boldsymbol{f}\left(\mathrm{x}_{t^{\prime}}, t^{\prime}\right) \text { for all } t, t^{\prime} \in[\epsilon, T]
f(xt,t)=f(xt′,t′) for all t,t′∈[ϵ,T]

consistency model的目标是从数据中估计一致性函数
f
f
f,来迫使self-consistency性质
一致性模型参数化
对于任意的一致性函数 f ( ⋅ , ⋅ ) f(\cdot, \cdot) f(⋅,⋅),用神经网络来拟合。但要满足两个条件:①同一个轨迹上的点输出一致;②在起始点f为一个对于x的恒等函数
- 第一种做法简单地参数化consistency models

- 第二种做法使用跳跃连接(作者和许多其他的都用这个)

一致性模型采样
有了训练好的一致性模型 f θ ( ⋅ , ⋅ ) f_\theta(\cdot, \cdot) fθ(⋅,⋅) ,就可以通过初始分布采样来产生样本。(这里指的是训练好后怎么来生成样本)

在一致性模型中,可以一步生成样本。也可以多步生成,算法1为多步生成。
想法就是预测出x后回退然后再进行预测减小误差。实际中,采用贪心算法来寻找时间点,通过三值搜索每次确定一个时间点,优化算法得到的样本的FID(不太重要)
Training Consistency Models via Distillation
第一种训练consistency model的方式——蒸馏预训练好的score model
s
ϕ
(
x
,
t
)
s_{\phi}(\mathrm{x}, t)
sϕ(x,t)
假设采样轨迹的时间序列为
t
1
=
ϵ
<
t
2
<
⋯
<
t
N
=
T
t_{1}=\epsilon<t_{2}<\cdots<t_{N}=T
t1=ϵ<t2<⋯<tN=T
通过运行数值ODE求解器的一个离散化步骤从
x
t
n
+
1
\mathbf{x}_{t_{n+1}}
xtn+1得到
x
t
n
\mathbf{x}_{t_{n}}
xtn
![]()
Φ
(
.
.
.
;
ϕ
)
\Phi(...;\phi)
Φ(...;ϕ)为ODE solver
例如使用Euler solver
d
x
d
t
=
−
t
s
ϕ
(
x
t
,
t
)
\frac{\mathrm{dx}}{\mathrm{d} t}=-t s_{\phi}\left(\mathrm{x}_{t}, t\right)
dtdx=−tsϕ(xt,t) ,
Φ
(
x
,
t
;
ϕ
)
=
−
t
s
ϕ
(
x
,
t
)
\Phi(\mathrm{x}, t ; \phi)=-t s_{\phi}(\mathrm{x}, t)
Φ(x,t;ϕ)=−tsϕ(x,t)带入上式得到
![]()
沿着ODE轨迹的分布进行第一次采样
x
\mathrm{x}
x~
p
d
a
t
a
p_{data}
pdata,然后添加高斯噪声,生成一对在PF ODE轨迹上相邻的数据点
(
x
^
t
n
ϕ
,
x
t
n
+
1
)
\left(\hat{\mathbf{x}}_{t_n}^\phi, \mathbf{x}_{t_{n+1}}\right)
(x^tnϕ,xtn+1)
通过最小化这一对的输出差异来训练一致性模型,作者遵循一致性蒸馏损失来训练一致性模型,就有如下的consistency distillation loss:

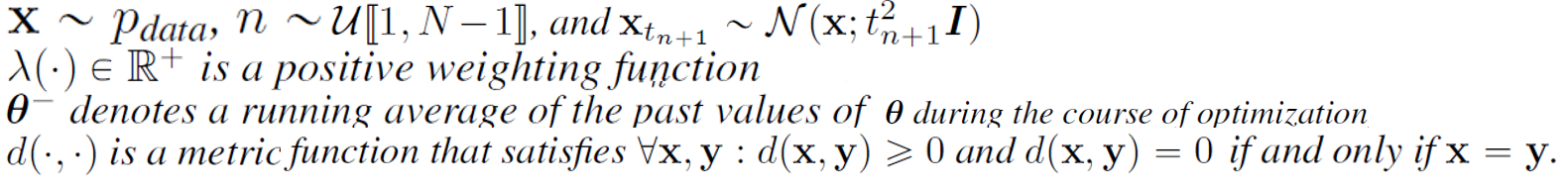
在蒸馏的过程中,作者用预训练模型来估计得分.
采用EMA来更新模型会提高训练的稳定性,并且性能会更好

Training Consistency Models in Isolation
Consistency models也可以单独进行训练,而不依赖于预训练好的扩散模型。
作者说这与扩散蒸馏技术不同,使一致性模型成为一个新的独立的生成模型家族。
在consistency distillation中,使用了预训练的score model
s
ϕ
(
x
,
t
)
s_{\phi}(\mathrm{x}, t)
sϕ(x,t)来近似ground truth score function
▽
l
o
g
p
t
(
x
)
\bigtriangledown logp_t(\mathbf{x})
▽logpt(x)。
作者证明了
▽
l
o
g
p
t
(
x
)
\bigtriangledown logp_t(\mathbf{x})
▽logpt(x)的一种无偏估计,即证明了一种新的得分函数的估计

即给定x, xt,可以用
−
(
x
t
−
x
)
/
t
2
-(\mathbf{x}_t -\mathbf{x})/t^2
−(xt−x)/t2 形式化
▽
l
o
g
p
t
(
x
)
\bigtriangledown logp_t(\mathbf{x})
▽logpt(x)的蒙特卡罗估计,可以理解为

利用该得分估计,作者构建了新的consistency training (CT) loss记作
L
C
T
N
(
θ
,
θ
−
)
L_{CT}^{N}(\theta,\theta^-)
LCTN(θ,θ−)