Pytorch对机器学习模型的安全漏洞攻击方法之Fast Gradient Sign Attack(FGSM,快速梯度符号攻击)

原论文：EXPLAINING AND HARNESSING ADVERSARIAL EXAMPLES
一般本人的习惯是先看论文熟悉它，然后代码去实现它，这样感觉要好点。因为论文讲解的比较全面和一些实验对比还有很多的引用等，另外大家知道好论文基本都是英文，所以对于英文弱点的伙伴们可能需要多花点时间去研读了。论文有论文的好处：全面，博客也有博客的好处：重点展示，以及代码的实现。

1、快速梯度符号攻击

攻防是一个永恒的主题，同样也适应在机器学习模型中，这也是一门热门话题：对抗性机器学习。

通过论文的阅读，我这里表达下自己对论文的理解(如有错误请指正)：FGSM是一种简单高效的对抗样本生成方法，通过计算loss对于输入的梯度为∇xJ(θ,x,y)，然后将其符号化，使用这个函数sign()，最后将符号化的梯度乘以一个小的扰动值ϵ，这个扰动值ϵ是一个超参数，从而生成肉眼难以察觉的对抗样本，让机器模型学习产生错误的分类结果。

我们先来看下一张“经典熊猫”图：

输入是一张“熊猫”，加了一些扰动之后，我们发现目标网络错误地将它归类为“长臂猿”了，而且这个置信度是99.3%，哈哈，这算不算迷之自信。所以说我们在设计和训练机器学习模型的时候，经常会忽视的方面是安全性和鲁棒性，特别是在面对希望欺骗模型的对手时，也就是说攻击模型，让这个模型的输出造成错误，比如分类错误。就是在我们的图像中添加不可察觉的扰动都会导致截然不同的模型性能。

本章将通过一个图像分类器的例子来探讨这个主题。具体来说，我们将使用一个最早最流行的攻击方法之一：快速梯度符号攻击(Fast Gradient Sign Attack)方法来欺骗MNIST分类器。
我们知道对于攻击分两种，白盒攻击和黑盒攻击，这里介绍的FGSM属于白盒攻击，而黑盒攻击的意思就是不清楚模型的架构和权重，只有输入和输出，也就是说模型对于攻击者来说是个黑盒子，不清楚里面的任何情况。

本人深度学习的第一个真正实例也是这个手写识别数字数据集MNIST，对于初次接触的可以先熟悉下这个数据集，很经典的例子，下面是一些MNIST相关文章，有兴趣的可以看看：
MNIST数据集手写数字识别（一）
MNIST数据集手写数字识别（二）
深度的卷积神经网络CNN（MNIST数据集示例）
卷积神经网络（CNN）之MNIST手写数字数据集的实现
这个攻击方法的示例来自于：https://github.com/pytorch/tutorials/blob/main/beginner_source/fgsm_tutorial.py
下面本人将对其进行一些通俗的解释，然后具体来看下是如何进行攻击的。最后通过可视化，让大家有个更直观的感受。

这里使用Jupyter Lab来测试，没有安装的可以安装来体验下，安装命令：

pip install jupyterlab -i http://pypi.douban.com/simple/  --trusted-host pypi.douban.com

安装好了之后，命令行输入启动命令即可：jupyter lab

2、MNIST模型

首先导入相关需要的库

from __future__ import print_function
import torch
import torch.nn as nn
import torch.nn.functional as F
import torch.optim as optim
from torchvision import datasets, transforms
import numpy as np
import matplotlib.pyplot as plt

这里使用的是PyTorch框架，如果你没有安装相关库，将报模块缺失的错误，然后安装的时候还是推荐使用加镜像安装，国内安装速度要快很多！

报错：ModuleNotFoundError: No module named 'torch'
安装命令：

pip install torch -i http://pypi.douban.com/simple/  --trusted-host pypi.douban.com

报错：ModuleNotFoundError: No module named 'torchvision'
安装命令：

pip install torchvision -i http://pypi.douban.com/simple/  --trusted-host pypi.douban.com

#这是一个hack，用来在下载MNIST数据集时绕过“User-agent”限制，看情况可选
from six.moves import urllib
opener = urllib.request.build_opener()
opener.addheaders = [('User-agent', 'Mozilla/5.0')]
urllib.request.install_opener(opener)

#这里的epsilons就是扰动量，随着这个值的增加，我们可以观察到它们的分类错误将越来越大
epsilons = [0, .05, .1, .15, .2, .25, .3]
pretrained_model = "data/lenet_mnist_model.pth"
use_cuda=True #由于这里使用的数据集比较小，所以使用CPU也是可以的

其中预训练模型下载：https://drive.google.com/drive/folders/1fn83DF14tWmit0RTKWRhPq5uVXt73e0h

当然这里需要科学上网，对于不方便的，我将其上传到了CSDN，点击下载：MNIST预训练模型.pth文件

# 定义被攻击的模型
class Net(nn.Module):
    def __init__(self):
        super(Net, self).__init__()
        self.conv1 = nn.Conv2d(1, 10, kernel_size=5)
        self.conv2 = nn.Conv2d(10, 20, kernel_size=5)
        self.conv2_drop = nn.Dropout2d()
        self.fc1 = nn.Linear(320, 50)
        self.fc2 = nn.Linear(50, 10)

    def forward(self, x):
        x = F.relu(F.max_pool2d(self.conv1(x), 2))
        x = F.relu(F.max_pool2d(self.conv2_drop(self.conv2(x)), 2))
        x = x.view(-1, 320)
        x = F.relu(self.fc1(x))
        x = F.dropout(x, training=self.training)
        x = self.fc2(x)
        return F.log_softmax(x, dim=1)

# MNIST Test dataset and dataloader declaration
test_loader = torch.utils.data.DataLoader(
    datasets.MNIST('../data', train=False, download=True, transform=transforms.Compose([
            transforms.ToTensor(),
            ])),
        batch_size=1, shuffle=True)

#CUDA Available:  False
print("CUDA Available: ",torch.cuda.is_available())
device = torch.device("cuda" if (use_cuda and torch.cuda.is_available()) else "cpu")

# 初始化模型
model = Net().to(device)

# 加载预训练模型的权重
model.load_state_dict(torch.load(pretrained_model, map_location='cpu'))

# 设置模型为评估模式
model.eval()

如果没有下载好MNIST数据集将先自动下载，然后初始化模型并加载预训练模型的权重。

'''
Net(
  (conv1): Conv2d(1, 10, kernel_size=(5, 5), stride=(1, 1))
  (conv2): Conv2d(10, 20, kernel_size=(5, 5), stride=(1, 1))
  (conv2_drop): Dropout2d(p=0.5, inplace=False)
  (fc1): Linear(in_features=320, out_features=50, bias=True)
  (fc2): Linear(in_features=50, out_features=10, bias=True)
)
'''

3、FGSM攻击函数

模型定义并初始化好了之后，我们就开始写FGSM的攻击代码
通过干扰原始输入来定义产生对抗性例子的函数，公式如下：
perturbed_image=image+epsilon∗sign(data_grad)=x+ϵ∗sign(∇xJ(θ,x,y))
另外为了保持数据的原始范围，将扰动后的图像裁剪到范围内[0,1]
代码如下：

def fgsm_attack(image, epsilon, data_grad):
    # 收集数据梯度的元素符号
    sign_data_grad = data_grad.sign()
    # 通过调整输入图像的每个像素来创建扰动图像
    perturbed_image = image + epsilon*sign_data_grad
    # 添加剪辑以保持[0,1]范围
    perturbed_image = torch.clamp(perturbed_image, 0, 1)
    return perturbed_image

4、攻击MNIST模型代码

def test( model, device, test_loader, epsilon ):
    # 正确的计数
    correct = 0
    adv_examples = []

    # 循环遍历测试集中的所有示例
    for data, target in test_loader:
        # 将数据和标签发送到设备
        data, target = data.to(device), target.to(device)
        # 设置张量的requires_grad属性。重要的进攻
        data.requires_grad = True

        output = model(data)
        init_pred = output.max(1, keepdim=True)[1] # 得到最大对数概率的索引

        # 如果最初的预测是错误的，不要攻击，继续前进
        if init_pred.item() != target.item():
            continue

        # 计算损失
        loss = F.nll_loss(output, target)

        # 梯度置零
        model.zero_grad()
        loss.backward()
        data_grad = data.grad.data

        # 调用上面写的FGSM攻击函数
        perturbed_data = fgsm_attack(data, epsilon, data_grad)
        # 重新分类扰动图像
        output = model(perturbed_data)

        final_pred = output.max(1, keepdim=True)[1]
        if final_pred.item() == target.item():
            correct += 1
            # 保存ε为0的例子
            if (epsilon == 0) and (len(adv_examples) < 5):
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )
        else:
            # 为了后面的可视化，保存一些对抗性例子(就是错误的分类)
            if len(adv_examples) < 5:
                adv_ex = perturbed_data.squeeze().detach().cpu().numpy()
                adv_examples.append( (init_pred.item(), final_pred.item(), adv_ex) )

    # 计算最终精度
    final_acc = correct/float(len(test_loader))
    print("Epsilon: {}\tTest Accuracy = {} / {} = {}".format(epsilon, correct, len(test_loader), final_acc))

    # 返回最终精度和对抗性例子
    return final_acc, adv_examples

5、运行攻击代码

accuracies = []
examples = []

# 为每个epsilon运行测试
for eps in epsilons:
    acc, ex = test(model, device, test_loader, eps)
    accuracies.append(acc)
    examples.append(ex)

'''
Epsilon: 0	Test Accuracy = 9810 / 10000 = 0.981
Epsilon: 0.05	Test Accuracy = 9426 / 10000 = 0.9426
Epsilon: 0.1	Test Accuracy = 8510 / 10000 = 0.851
Epsilon: 0.15	Test Accuracy = 6826 / 10000 = 0.6826
Epsilon: 0.2	Test Accuracy = 4301 / 10000 = 0.4301
Epsilon: 0.25	Test Accuracy = 2082 / 10000 = 0.2082
Epsilon: 0.3	Test Accuracy = 869 / 10000 = 0.0869
'''

可以看到随着ε的增加，准确率是越来越低了。

6、精度的可视化

我们将上面的迭代数据做一个可视化，更直观的感受下：

plt.figure(figsize=(5,5))
plt.plot(epsilons, accuracies, "*-")
plt.yticks(np.arange(0, 1.1, step=0.1))
plt.xticks(np.arange(0, .35, step=0.05))
plt.title("Accuracy vs Epsilon")
plt.xlabel("Epsilon")
plt.ylabel("Accuracy")
plt.show()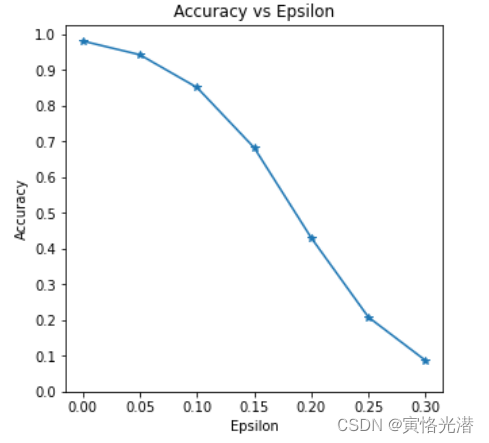

7、对抗性示例

最后我们在每个epsilon上绘制几个对抗性样本的例子来感受下，原始分类 -> 对抗分类

cnt = 0
plt.figure(figsize=(8,10))
for i in range(len(epsilons)):
    for j in range(len(examples[i])):
        cnt += 1
        plt.subplot(len(epsilons),len(examples[0]),cnt)
        plt.xticks([], [])
        plt.yticks([], [])
        if j == 0:
            plt.ylabel("Eps: {}".format(epsilons[i]), fontsize=14)
        orig,adv,ex = examples[i][j]
        plt.title("{} -> {}".format(orig, adv))
        plt.imshow(ex, cmap="gray")
plt.tight_layout()
plt.show()