题意
求把 N×M 的棋盘分割成若干个 1×2 的长方形,有多少种方案。
例如当 N=2,M=4 时,共有 5 种方案。当 N=2,M=3 时,共有 3 种方案。
如下图所示:

输入格式
输入包含多组测试用例。
每组测试用例占一行,包含两个整数 N 和 M。
当输入用例 N=0,M=0,表示输入终止,且该用例无需处理。
输出格式
每个测试用例输出一个结果,每个结果占一行。
数据范围
1≤N,M≤11
输入样例:
1 2
1 3
1 4
2 2
2 3
2 4
2 11
4 11
0 0
输出样例:
1
0
1
2
3
5
144
51205思路
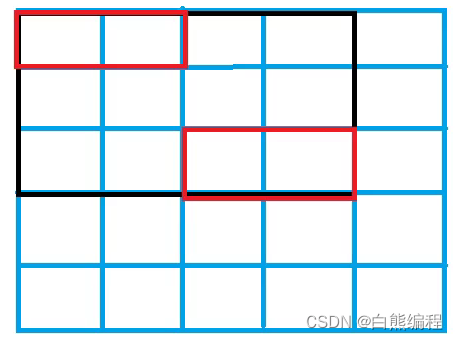
当把所有横向小方格放完后,纵向小方格一定只有一种情况放法。
所以,总摆放方案数=横向小方格摆放数总和。
3*4方格案例: 红色为所有横向小方格所放位置,剩余位置纵向只有一种情况放法。
分析
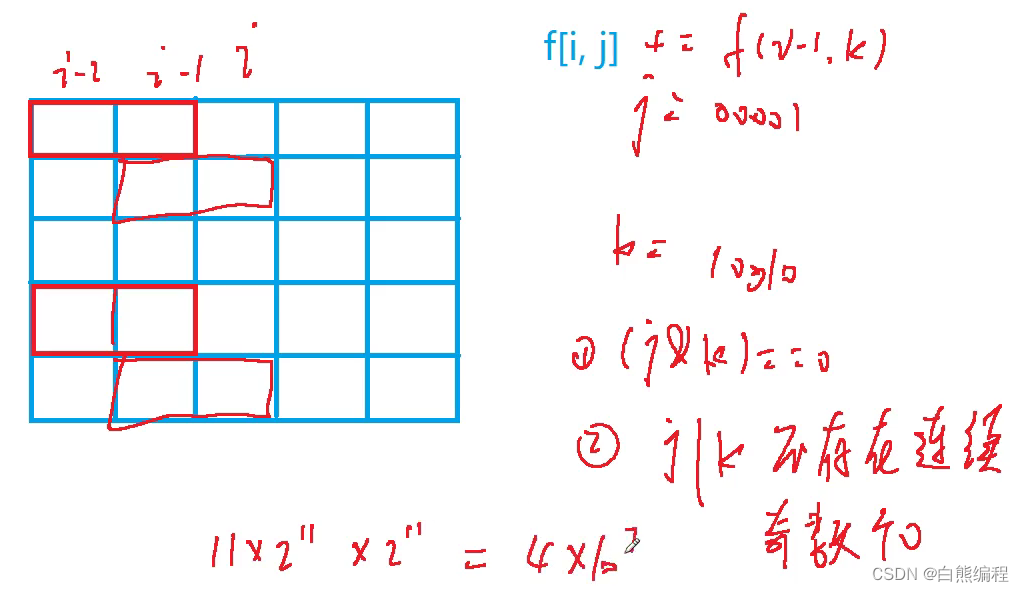
dp[i][j]表示在第i列中,第i-1列横向伸出到第i列的小方格序列是j(j是一个二进制数)的情况。
转移条件
1.第i-2列伸到第i-1列的小方格序列k和第i-1列伸到第i列的小方格序列j不能冲突,即j&k==0;
2.第i列中剩余的连续空白格子一定是偶数,即j|k状态不能出现连续奇数个0。
综上,满足以上条件则说明第i列可由第i-1列转移过来,对应一种方案,则方案数为dp[i][j]+=dp[i-1][k]。
代码
#include<iostream>
#include<algorithm>
#include<cstring>
using namespace std;
typedef long long LL;
const int N=12,M=1<<N;
int n,m;
LL dp[N][M];
bool st[M];
int main(){
std::ios::sync_with_stdio(false),std::cin.tie(nullptr),std::cout.tie(nullptr);
int n,m;
while(cin>>n>>m,m||n){
memset(dp,0,sizeof dp);
for(int i=0;i<1<<n;i++){
st[i]=true;
int cnt=0;
for(int j=0;j<n;j++){
if(i>>j&1){
if(cnt&1)st[i]=false;
cnt=0;
}else cnt++;
}
if(cnt&1)st[i]=false;
}
dp[0][0]=1;
for(int i=1;i<=m;i++){
for(int j=0;j<1<<n;j++){
for(int k=0;k<1<<n;k++){
if((j&k)==0&&st[j|k]){
dp[i][j]+=dp[i-1][k];
}
}
}
}
cout<<dp[m][0]<<endl;
}
return 0;
}