题目：119. 杨辉三角II

我的解法：先将杨辉三角存储起来，取出第rowIndex行

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<vector<int>> ans(rowIndex+1);	//初始化rowIndex+1行的杨辉三角
        for(int i=0; i<rowIndex+1; ++i){
            ans[i].resize(i+1);	//每一行初始化i+1个元素
            ans[i][0] = ans[i][i] = 1;	//首末元素=1
            for(int j=1; j<i; ++j){	//其他元素为i-1行的第j-1个元素和第j个元素的和
                    ans[i][j] = ans[i-1][j] + ans[i-1][j-1];
            }
        }
        return ans[rowIndex];	//取出第rowIndex行
    }
};

其他解法：公式法

$$C_n^m=\frac{n!}{m!(n-m)!}$$
$$C_n^m=C_n^{m-1}\times \frac{n-m+1}{m}$$

class Solution {
public:
    vector<int> getRow(int rowIndex) {
        vector<int> ans(rowIndex+1);
        ans[0]=1;
        for(int i=1; i<rowIndex+1; ++i){
            ans[i] = 1LL * ans[i-1] * (rowIndex - i + 1)/i;  //1LL是将32位运算转换为64位Long Long类型，防止溢出，必须写在最前面，这里n=rowIndex，m=i
        }
        return ans;
    }
};

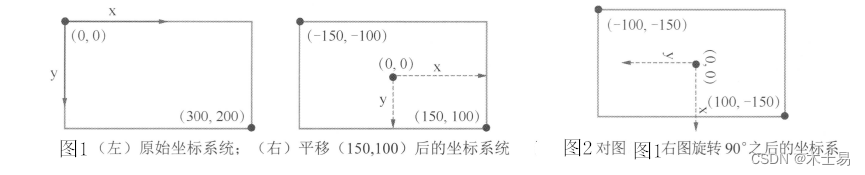
题目：48. 旋转图像

解法1：找规律

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        for(int i=0; i<n/2; ++i){
            for(int j=i; j<n-i-1; ++j){
                int temp = matrix[i][j];
                matrix[i][j] = matrix[n-j-1][i];
                matrix[n-j-1][i] = matrix[n-i-1][n-j-1];
                matrix[n-i-1][n-j-1] = matrix[j][n-i-1];
                matrix[j][n-i-1] = temp;
            }
        }
    }
};

解法2：先水平翻转，再对角线交换

class Solution {
public:
    void rotate(vector<vector<int>>& matrix) {
        int n = matrix.size();
        //水平翻转
        for(int i=0; i<n/2; ++i){
            for(int j=0; j<n; ++j){
                swap(matrix[i][j], matrix[n-i-1][j]);
            }
        }
        //对角线调换
        for(int i=0; i<n; ++i){
            for(int j=0; j<i; ++j){	//注意这里j<i
                swap(matrix[i][j], matrix[j][i]);
            }
        }
    }
};

题目：59. 螺旋矩阵II

解法：设置left、right、top、bottom四条辅助线

class Solution {
public:
    vector<vector<int>> generateMatrix(int n) {
        vector<vector<int>> ans(n, vector<int>(n));
        //设置四条辅助线
        int l=0, r=n-1, t=0, b=n-1, p=1;
        while(p<=n*n){
            for(int i=l; i<=r; ++i){	//同一top，左到右
                ans[t][i]=p; ++p;
            }
            ++t;
            for(int i=t; i<=b; ++i){	//同一right，上到下
                ans[i][r]=p; ++p;
            }
            --r;
            for(int i=r; i>=l; --i){	//同一bottom，右到左
                ans[b][i]=p; ++p;
            }
            --b;
            for(int i=b; i>=t; --i){	//同一left，下到上
                ans[i][l]=p; ++p;
            }
            ++l;
        }
        return ans;
    }
};