常量折叠

基本思想：在编译期间计算表达式的值（编译时静态计算）

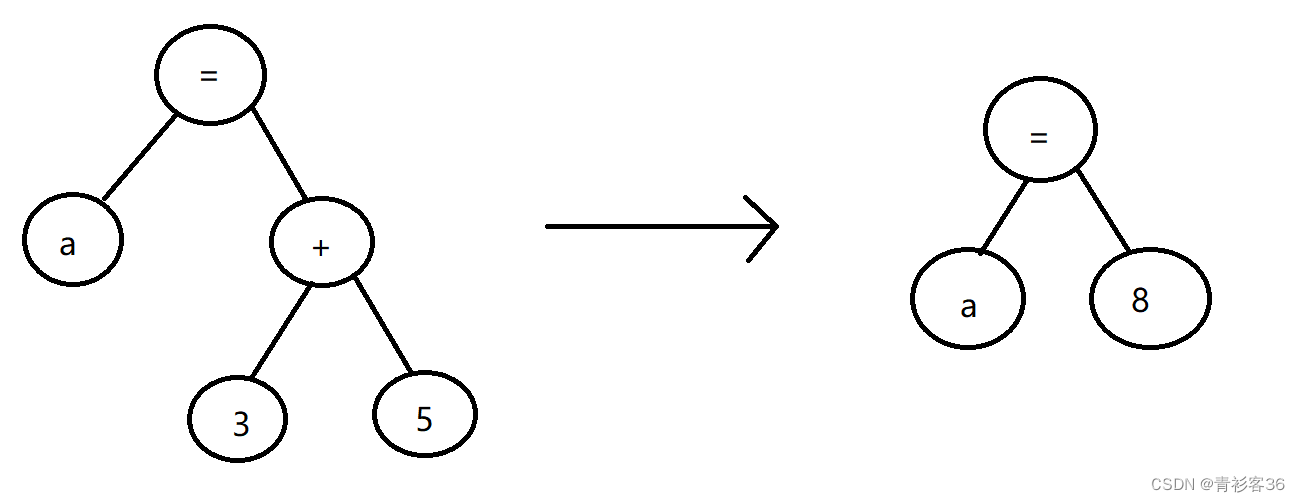
例如：a = 3 + 5 ==> a = 8，if (true && false) ... ==> if (false)

好处是：语法树的节点数量减少了，意味着编译器要维护的中间表示所要耗费的计算资源（比如内存）减少了；将来生成机器码的话，指令也减少了。

常量折叠把进行更深层次的优化的机会暴露出来了，例如上面的if （false），就可以进行死代码消除优化。

可以整型、布尔型、浮点型等数据类型上进行（依赖于我们编译的元语言的情况） 

语法制导的常量折叠算法

const_foid(Exp_t e)
{
    while (e is stiil shrinking)
        switch (e->kind)
            case EXP_ADD:
                Exp_t l = e->left;
                Exp_t r = e->right;
                if (l->kind == EXP_NUM && r->kind == EXP_NUM)
                    e = Exp_Num _new(l->value + r->value);
                break;
            case EXP_TIMES:
                ...
            default:
                break;
}

常量折叠小结

容易实现、可以在语法树或者中间表示上进行

通常被实现成公共子函数被其他优化调用

必须要很小心遵守语言的定义，例如：考虑溢出或者异常，0xffffffff+1 ==> 0 （要考虑整型数的溢出是否要抛异常？不能直接优化掉！）

代数化简

基本思想：利用代数系统的性质对程序进行化简

示例：

a = 0 + b    ==>    a = b        （0是加法的左零元）
a = 1 * b    ==>    a = b         （1是乘法的左单位元）
2 * a          ==>    a + a         （强度削弱）
2 * a          ==>    a << 1       （强度削弱）

同样必须非常仔细的处理语义

例如：(i - j) + (i - j)    ==>    i + i - j - j，其中i = j = 0xffffffff，优化前为0，优化后i + i溢出，抛出异常

语法制导的代数化简算法

alg_simp(Exp_t e)
{
    whiie(e is sti11 shrinking) 
        switch (e->kind)
            caseEXP_ADD : 
                Exp_t l = e->left;
                Exp_t r = e->right;
                if (l->kind == EXP_NUM && l->value == 0)
                    e = r;
                break;
            case...:
                ...;  // 类似
}

死代码（不可达代码）删除

基本思想：静态移除程序中不可执行的代码

示例：if (false)  s1;  else  s2;   ==>   s2;

在控制流图上也可以进行这些优化，但在早期做这些优化可以简化中后端

不可达代码删除算法

deadcode(Stm_t s)
{
    while (s is still shrinking)
        switch (s->kind)
            case STM_IF:
                Exp_t e = s->condition;
                if (e->kind == EXP_FALSE)
                    s = s->elsee;
                break;
            case ...:
                ...; // 类似
}