前言

小亭子正在努力的学习编程，接下来将开启算法的学习~~

分享的文章都是学习的笔记和感悟，如有不妥之处希望大佬们批评指正~~

同时如果本文对你有帮助的话，烦请收藏点赞关注支持一波, 感激不尽~~

刷题专栏在这里~~

深入理解动态规划建议关注刷题专栏，看一下前面几篇关于动态规划理论的文章

分割等和子集

、刷题链接

给定一个只包含正整数的非空数组。是否可以将这个数组分割成两个子集，使得两个子集的元素和相等。

注意: 每个数组中的元素不会超过 100 数组的大小不会超过 200

示例 1:

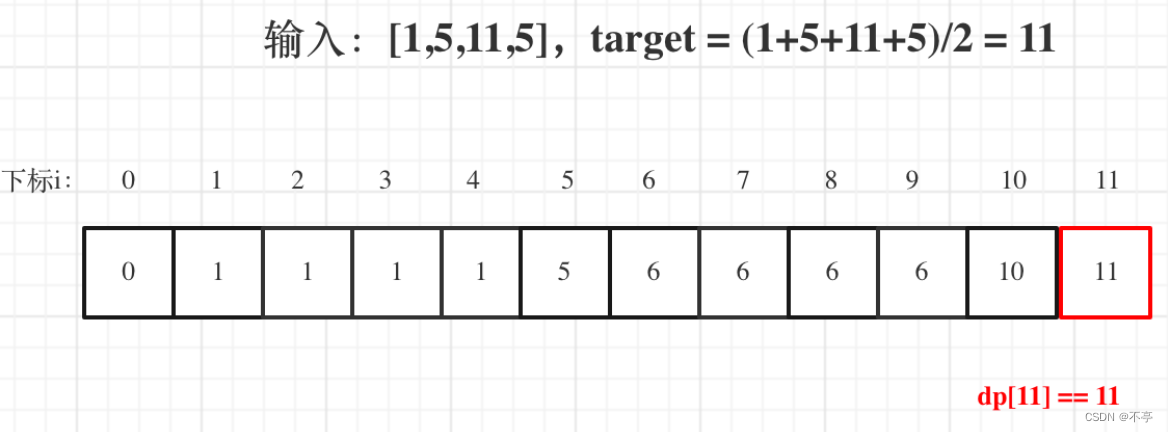
• 输入: [1, 5, 11, 5]
• 输出: true
• 解释: 数组可以分割成 [1, 5, 5] 和 [11].

示例 2:

• 输入: [1, 2, 3, 5]
• 输出: false
• 解释: 数组不能分割成两个元素和相等的子集.

提示：

• 1 <= nums.length <= 200
• 1 <= nums[i] <= 100

题目分析：

本题我们可以用回溯法暴力搜索解题，但是这里主要介绍用动归的思想解题

首先，要用01背包问题的思路解题，我们需要知道背包的体积（容量），背包要放入的物品的价值，背包中的每一个元素不能重复放入

然后，将01背包问题套到本题上来：

• 背包的体积为sum / 2  （因为题目要求两个子集元素和相等）
• 背包要放入的商品（集合里的元素）重量为 元素的数值，价值也为元素的数值
• 背包如果正好装满，说明找到了总和为 sum / 2 的子集。
• 背包中每一个元素是不可重复放入

动规五部曲分析如下：

1.确定dp数组以及下标的含义

dp[j] 表示： 容量为 j 的背包，所背的物品价值最大可以为 dp[j]。

注意：本题中每一个元素的数值既是重量，也是价值。

套到本题，dp[j]表示 背包总容量（所能装的总重量）是j，放进物品后，背的最大重量为dp[j]。

那么如果背包容量为target， dp[target]就是装满 背包之后的重量

所以 当 dp[target] == target 的时候，背包就装满了。如果最后不相等，说明数组不能分割成两个元素和相等的子集。

2.确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题，相当于背包里放入数值，那么物品i的重量是nums[i]，其价值也是nums[i]。

所以递推公式：dp[j] = max(dp[j], dp[j - nums[i]] + nums[i]);

3.dp数组如何初始化

在01背包，一维dp如何初始化，前面的文章中已经详细说明了。

从dp[j]的定义来看，首先dp[0]一定是0。

如果题目给的价值都是正整数那么非0下标都初始化为0就可以了，如果题目给的价值有负数，那么非0下标就要初始化为负无穷。

这样才能让dp数组在递推的过程中取得最大的价值，而不是被初始值覆盖了。

但是：

本题题目中 只包含正整数的非空数组，所以非0下标的元素初始化为0就可以了。

4.确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！（前面的滚动数组已经详细介绍了）

5.举例推导dp数组

dp[j]的数值一定是小于等于j的。

如果dp[j] == j 说明，集合中的子集总和正好可以凑成总和j，理解这一点很重要。

用例1，输入[1,5,11,5] 为例，如图：

 最后dp[11] == 11，说明可以将这个数组分割成两个子集，使得两个子集的元素和相等。

java代码实现：

class Solution {
    public boolean canPartition(int[] nums) {
        /*判断是否为空,为空返回false,因为题目说了非空,所以这步可以省
       if(nums == null || nums.length == 0) 
       {
           return false;
              }
              */
    int sum =0;
       int n = nums.length;
       for(int num :nums){
           sum+=num;
       }
       //不能整除2,说明不能分成两个和相同的数组
        if(sum%2 != 0) {return false;}
       int target = sum/2;
       //定义dp数组
       int[] dp = new int[target+1];
       for(int i = 0 ; i < n ; i++){
           for(int j = target ; j >= nums[i] ; j--){
               dp[j] = Math.max(dp[j],dp[j-nums[i]]+nums[i]);

           }

       }
       //最后再判断得到的dp数组的值是否等于需要的背包容量
       return dp[target] == target;
     
          }

    }

• 时间复杂度：O(n^2)
• 空间复杂度：O(n)，虽然dp数组大小为一个常数，但是大常数

最后一块石头的重量II

刷题链接

有一堆石头，每块石头的重量都是正整数。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；

如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。

最后，最多只会剩下一块石头。返回此石头最小的可能重量。如果没有石头剩下，就返回 0。

示例：

• 输入：[2,7,4,1,8,1]
• 输出：1

解释：

• 组合 2 和 4，得到 2，所以数组转化为 [2,7,1,8,1]，
• 组合 7 和 8，得到 1，所以数组转化为 [2,1,1,1]，
• 组合 2 和 1，得到 1，所以数组转化为 [1,1,1]，
• 组合 1 和 1，得到 0，所以数组转化为 [1]，这就是最优值。

提示：

• 1 <= stones.length <= 30
• 1 <= stones[i] <= 1000

分析：

这个题和上一个问题，分割等和子集的问题非常像

对应01背包里的物品重量weight[i]和 物品价值value[i]。

本题物品的重量为stones[i]，物品的价值也为stones[i]。

可以把本题也分成两个子集，两个子集和最相近的子集，他们 的和 相减，就是剩下那块石头的最小重量。

动规五步曲：

1.确定dp数组以及下标的含义

dp[j]表示容量（这里说容量更形象，其实就是重量）为j的背包，最多可以背最大重量为dp[j]。

可以回忆一下01背包中，dp[j]的含义，容量为j的背包，最多可以装的价值为 dp[j]。

相对于 01背包，本题中，石头的重量是 stones[i]，石头的价值也是 stones[i] ，可以 “最多可以装的价值为 dp[j]” == “最多可以背的重量为dp[j]”

2.确定递推公式

01背包的递推公式为：dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);

本题则是：dp[j] = max(dp[j], dp[j - stones[i]] + stones[i]);

3.dp数组如何初始化

既然 dp[j]中的j表示容量，那么最大容量（重量）是多少呢，就是所有石头的重量和。

因为提示中给出1 <= stones.length <= 30，1 <= stones[i] <= 1000，所以最大重量就是30 * 1000 。

而我们要求的target其实只是最大重量的一半，所以dp数组开到15000大小就可以了。

当然也可以把石头遍历一遍，计算出石头总重量 然后除2，得到dp数组的大小。

我这里就直接用15000了。

4.确定遍历顺序

如果使用一维dp数组，物品遍历的for循环放在外层，遍历背包的for循环放在内层，且内层for循环倒序遍历！【具体原因请看滚动数组那篇文章】

5.举例推导dp数组

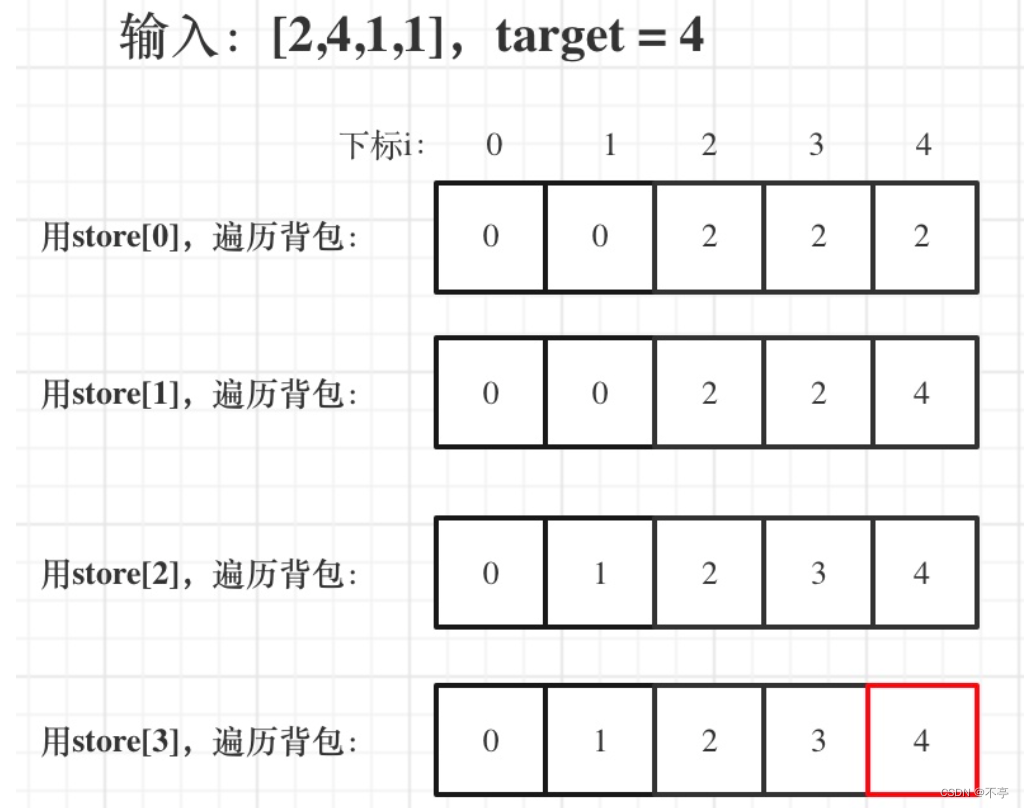
举例，输入：[2,4,1,1]，此时target = (2 + 4 + 1 + 1)/2 = 4 ，dp数组状态图如下：

最后dp[target]里是容量为target的背包所能背的最大重量。

那么分成两堆石头，一堆石头的总重量是dp[target]，另一堆就是sum - dp[target]。

在计算target的时候，target = sum / 2 因为是向下取整，所以sum - dp[target] 一定是大于等于dp[target]的。

那么相撞之后剩下的最小石头重量就是 (sum - dp[target]) - dp[target]。

代码如下：

class Solution {
    public int lastStoneWeightII(int[] stones) {
        int sum = 0;
        for(int i : stones){
            sum+=i;
        }
        int target = sum/2;
        //初始化dp数组
        int[] dp = new int[target+1];
        for(int i =0 ; i < stones.length; i++){
            for(int j = target ; j >= stones[i] ; j--){

                dp[j] = Math.max(dp[j],dp[j-stones[i]]+stones[i]);
            }
        }
        /*
        最后一块石头的重量等于 
        sum - dp[target] 是 另外一半石头的重量
        (sum - dp[target] )- dp[target];
        */
        return sum - dp[target] - dp[target];
           }
           
}

• 时间复杂度：O(m × n) , m是石头总重量（准确的说是总重量的一半），n为石头块数
• 空间复杂度：O(m)