222.完全二叉树的节点个数

给你一棵 完全二叉树 的根节点 root ，求出该树的节点个数。

完全二叉树 的定义如下：在完全二叉树中，除了最底层节点可能没填满外，其余每层节点数都达到最大值，并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层，则该层包含 1~ 2h 个节点。
链接：https://leetcode.cn/problems/count-complete-tree-nodes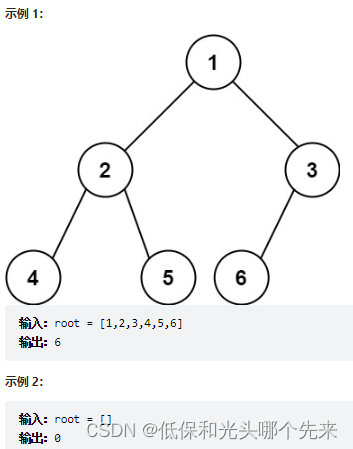

var countNodes = function(root) {
    var res = [], queue = [];
    var sumLen = 0;
    if(!root) return 0;
    queue.push(root);
    while(queue.length) {
        let len = queue.length;
        let curNode = [];
        for(let i = 0;i < len; i++) {
            let node = queue.shift();
            curNode.push(node.val);
            node.left && queue.push(node.left);
            node.right && queue.push(node.right);
        }
        res.push(curNode);
        sumLen += curNode.length;
    }
    return sumLen;
};

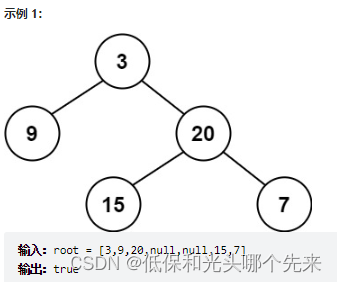
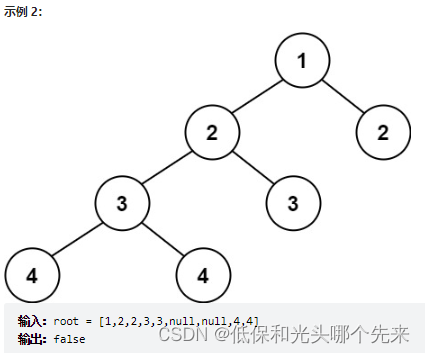
110.平衡二叉树

给定一个二叉树，判断它是否是高度平衡的二叉树。

本题中，一棵高度平衡二叉树定义为：

一个二叉树每个节点 的左右两个子树的高度差的绝对值不超过 1 。

var isBalanced = function(root) {
    return booleanisBalanced(root) != -1;
};
var booleanisBalanced = function(root) {
    if (!root) return 0;
    // 当某一子树不平衡就返回
    let left = booleanisBalanced(root.left);
    if (left == -1) return -1;
    let right = booleanisBalanced(root.right);
    if (right == -1) return -1;
    // 如果左右子树层高相差小于2  平衡：返回实际层高  否则返回-1
    return Math.abs(left - right) < 2 ? Math.max(left, right) + 1 : -1;
};

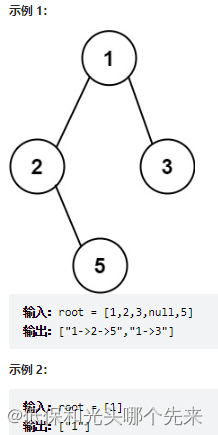
257. 二叉树的所有路径

给你一个二叉树的根节点 root ，按 任意顺序 ，返回所有从根节点到叶子节点的路径。

叶子节点 是指没有子节点的节点。

链接：力扣

var binaryTreePaths = function(root) {
    // 如果是空树
    if(!root) return [];
    var res = [], cur = '';
    pathNode(root, res, cur);
    return res;
};
var pathNode = (root, res, cur) => {
    if(!root) return;
    // 如果没有左右孩子，说明是叶子节点
    if(!root.left && !root.right) {
        // 在当前字符串上加上叶子结点
        cur += root.val;
        res.push(cur);
        return;
    }
    // 非叶子节点加 →
    else cur += root.val + '->';
    //递归左子树
    pathNode(root.left, res, cur);
    //递归右子树
    pathNode(root.right, res, cur);
}

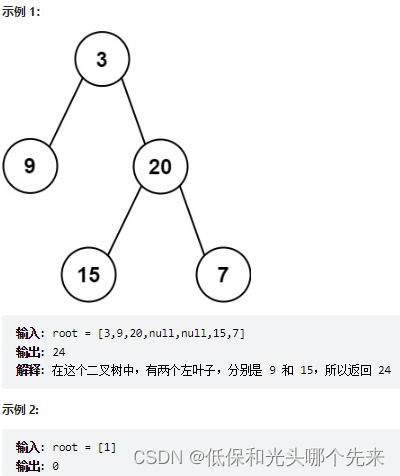
404.左叶子之和

给定二叉树的根节点 root ，返回所有左叶子之和。

链接：力扣

// 迭代
var sumOfLeftLeaves = function(root) {
    if(!root) return null;
    var list = [root], sum = 0;
    while(list.length) {
        var cur = list.shift();
        // 左节点是叶子节点时
        if(cur.left && !cur.left.left && !cur.left.right) 
            sum += cur.left.val;
        // 遍历左右子树
        cur.left && list.push(cur.left);
        cur.right && list.push(cur.right);
    }
    return sum;
};

 或

// 递归
var sumOfLeftLeaves = function(root) {
    return sumNode(root);
};
var sumNode = (root) => {
    if(!root) return null;
    // 遍历左右子树
    var lval = sumNode(root.left);
    var rval = sumNode(root.right);
    // 单层递归
    var mid = 0;
    // 当前是左叶子节点
    if(root.left && !root.left.left && !root.left.right) mid += root.left.val;
    // 左子树的左叶子节点+右子树的左叶子节点
    var sum = mid + lval + rval;
    return sum;
}

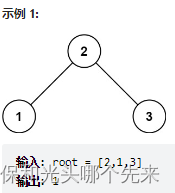
513.找树左下角的值

给定一个二叉树的 根节点 root，请找出该二叉树的 最底层 最左边 节点的值。

假设二叉树中至少有一个节点。

链接：力扣

var findBottomLeftValue = function(root) {
    var list = [root], res = 0;
    while(list.length) {
        var len = list.length;
        for(var i = 0; i < len; i++) {
            var cur = list.shift();
            if(i == 0) res = cur.val;
            cur.left && list.push(cur.left);
            cur.right && list.push(cur.right);
        }
    }
    return res;
};

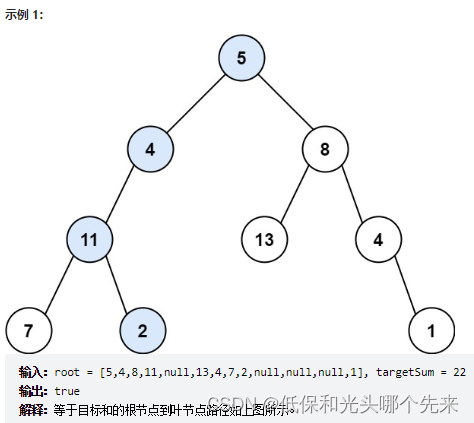
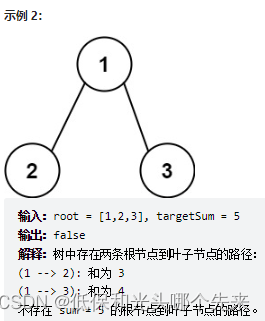
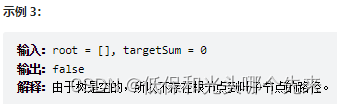
112. 路径总和

给你二叉树的根节点 root 和一个表示目标和的整数 targetSum 。判断该树中是否存在 根节点到叶子节点 的路径，这条路径上所有节点值相加等于目标和 targetSum 。如果存在，返回 true ；否则，返回 false 。

叶子节点 是指没有子节点的节点。
链接：https://leetcode.cn/problems/path-sum

  

var hasPathSum = function(root, targetSum) {
    var sum = 0;
    return pathSum(root, sum, targetSum);
};
var pathSum = (root, sum, targetSum) => {
    if(!root) return false;
    // 如果没有左右孩子，说明是叶子节点
    if(!root.left && !root.right) {
        // 在当前和上加上叶子结点的值为当前路径的sum
        sum += root.val;
        return sum == targetSum ? true : false;
    }
    // 非叶子节点只进行相加
    else sum += root.val;
    // 遍历左右子树
    return pathSum(root.left, sum, targetSum) || pathSum(root.right, sum, targetSum);  
}

106.从中序与后序遍历序列构造二叉树 

给定两个整数数组 inorder 和 postorder ，其中 inorder 是二叉树的中序遍历， postorder 是同一棵树的后序遍历，请你构造并返回这颗 二叉树 。
链接：https://leetcode.cn/problems/construct-binary-tree-from-inorder-and-postorder-traversal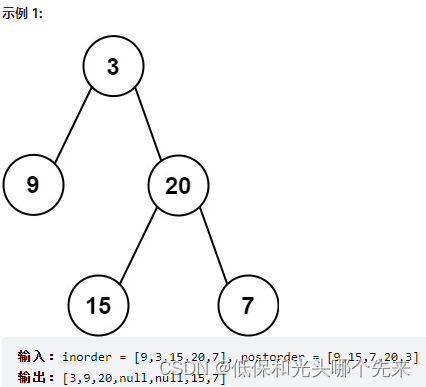

var buildTree = function(inorder, postorder) { 
    if(!inorder.length) return null;
    // 根节点是后序遍历的最后一个元素
    var rootVal = postorder[postorder.length-1];
    // 切割遍历数组的下标
    var index = inorder.indexOf(rootVal);
    // 中序左数组
    var midLeft = inorder.slice(0, index);
    // 中序右数组
    var midRight = inorder.slice(index+1, inorder.length);
    // 后序左数组
    var lastLeft = postorder.slice(0, index);
    // 后序右数组
    var lastRight = postorder.slice(index, postorder.length-1);
    // 创建二叉树
    var root = new TreeNode(rootVal);
    // 创建左子树
    root.left = buildTree(midLeft, lastLeft);
    // 创建右子树
    root.right = buildTree(midRight, lastRight);
    return root;
};

105.从前序与中序遍历序列构造二叉树

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。
链接：https://leetcode.cn/problems/construct-binary-tree-from-preorder-and-inorder-traversal

  

var buildTree = function(preorder, inorder) {
    if(!inorder.length) return null;
    // 根节点是前序遍历的第一个元素
    var rootVal = preorder[0];
    // 切割遍历数组的下标
    var index = inorder.indexOf(rootVal);
    // 中序左数组
    var midLeft = inorder.slice(0, index);
    // 中序右数组
    var midRight = inorder.slice(index+1, inorder.length);
    // 前序左数组
    var preLeft = preorder.slice(1, midLeft.length+1);
    // 前序右数组
    var preRight = preorder.slice(midLeft.length+1, preorder.length);
    // 创建二叉树
    var root = new TreeNode(rootVal);
    // 创建左子树
    root.left = buildTree(preLeft, midLeft);
    // 创建右子树
    root.right = buildTree(preRight, midRight);
    return root;
};

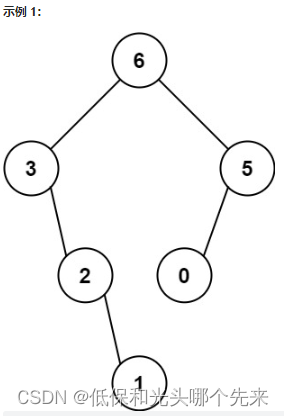
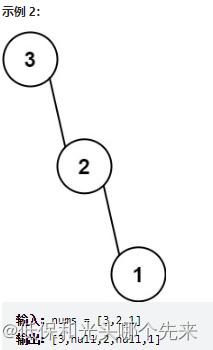
654.最大二叉树

给定一个不重复的整数数组 nums 。 最大二叉树 可以用下面的算法从 nums 递归地构建:

创建一个根节点，其值为 nums 中的最大值。
递归地在最大值 左边 的 子数组前缀上 构建左子树。
递归地在最大值 右边 的 子数组后缀上 构建右子树。
返回 nums 构建的 最大二叉树 。
链接：https://leetcode.cn/problems/maximum-binary-tree

var constructMaximumBinaryTree = function(nums) {
    var root = maxVal(nums, 0, nums.length-1);
    return root;
};
var maxVal = (list, left, right) => {
    if(left > right) return null;
    let tarVal = -1, tarIndex = -1;
    for(var i = left; i <= right; ++i) {
        if(list[i] > tarVal) {
            tarVal = list[i];
            tarIndex = i;
        }
    }
    var root = new TreeNode(tarVal);
    root.left = maxVal(list, left, tarIndex-1);
    root.right = maxVal(list, tarIndex + 1, right);
    return root;
}