最长公共上升子序列LCIS

题目链接: acwing272. 最长公共上升子序列
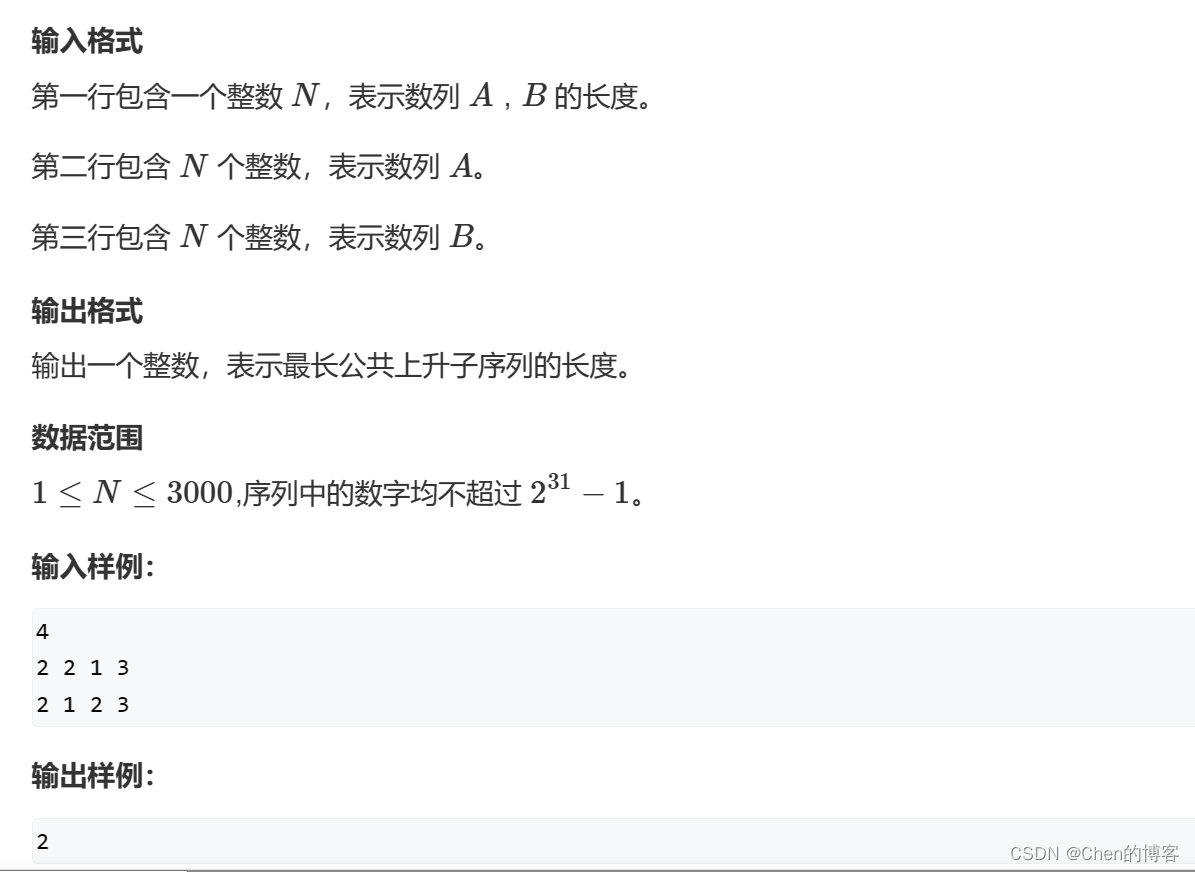
题目描述:

输入输出:

题解:
首先考虑 最长上升子序列和 最长公共子序列问题
最长上升子序列的状态表示与状态转移如下:

状态表示:
用f[i],来表示以A[i]结尾的A[1~i]最长上升子序列的长度(注意，该上升子序列结尾为A[i])
状态转移:
mx=0
for(int k=1;k<i;k++)
	if(A[k]<A[i]) mx=max(mx,f[k]);
f[i]=mx+1;

最长公共子序列的状态表示与状态转移如下:

状态表示:
用f[i][j]来表示A[1~i]与B[1~j]的最长公共子序列
状态转移:
if(A[i]==B[j]) f[i][j]=f[i-1][j-1]+1;
else f[i][j]=max(f[i-1][j],f[i][j-1]);

由上面的这两个，我们来写最长公共上升子序列LCIS的状态表示与状态转移:

状态表示:
用f[i][j]来表示以B[j]为结尾(结尾为B[j])的A[1~i]与B[1~j]的最长公共上升子序列长度
状态转移:
考虑两种情况:
if(A[i]!=B[j]) f[i][j]=f[i-1][j];//这个很好理解,如果A[i]!=B[j],
//那么以B[j]为结尾(结尾为B[j])的A[1~i]与B[1~j]的最长公共上升子序列一定在A[1~i-1]与B[1~j]中
else{
	//此时A[i]==B[j],我们要在A[1~i-1]与B[1~j-1]中到一个最长的公共上升子序列,并且子序列的结尾还要小于B[j]==A[i]，
	//这样才能将A[i]与B[j]接在其后面
	mx=0;
	for(int k=1;k<j;k++)
		if(B[k]<B[j]) mx=max(mx,f[i-1][j]);//这里B[j]==A[i],判断条件中也能写成A[i](用于后续优化)
	f[i][j]=mx+1;
}

代码如下:$O(n^3)$

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=3010;
int f[N][N];
int main(){
    int n;
    int A[N],B[N];
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&A[i]);
    for(int i=1;i<=n;i++) scanf("%d",&B[i]);
    for(int i=1;i<=n;i++){
        for(int j=1;j<=n;j++){
            if(A[i]!=B[j]) f[i][j]=f[i-1][j];
            else{
                int mx=0;
                for(int k=1;k<j;k++)
                    if(A[i]>B[k]) mx=max(mx,f[i-1][k]);
                f[i][j]=mx+1;
            } 
        }
    }
    int t=0;
    for(int i=1;i<=n;i++)
        if(f[n][i]>t) t=f[n][i];
    cout<<t;
    return 0;
}

我们考虑对代码进行优化，可以在第二层循环中顺便求出A[i]>B[k]的最大值
代码如下:$O(n^2)$

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
using namespace std;
const int N=3010;
int f[N][N];
int main(){
    int n;
    int A[N],B[N];
    cin>>n;
    for(int i=1;i<=n;i++) scanf("%d",&A[i]);
    for(int i=1;i<=n;i++) scanf("%d",&B[i]);
    for(int i=1;i<=n;i++){
        int mx=0;
        for(int j=1;j<=n;j++){
            if(A[i]!=B[j]) f[i][j]=f[i-1][j];
            else f[i][j]=mx+1;
            if(B[j]<A[i]) mx=max(mx,f[i-1][j]);
        }
    }
    int t=0;
    for(int i=1;i<=n;i++)
        if(f[n][i]>t) t=f[n][i];
    cout<<t;
    return 0;
}

参考博客