最小生成树跟边的正负没有任何关系。

最小生成树

朴素Prime

该算法和Dijkstr算法很像。

先把所有距离初始化为正无穷

进行n次迭代

找到不在集合（集合指当前的生成树）当中的点，s数组表示当前已经在连通块（生成树）中的所有点。

找到集合外距离最近的点赋给t，用t更新其它点到集合的距离

s加入到t当中去。

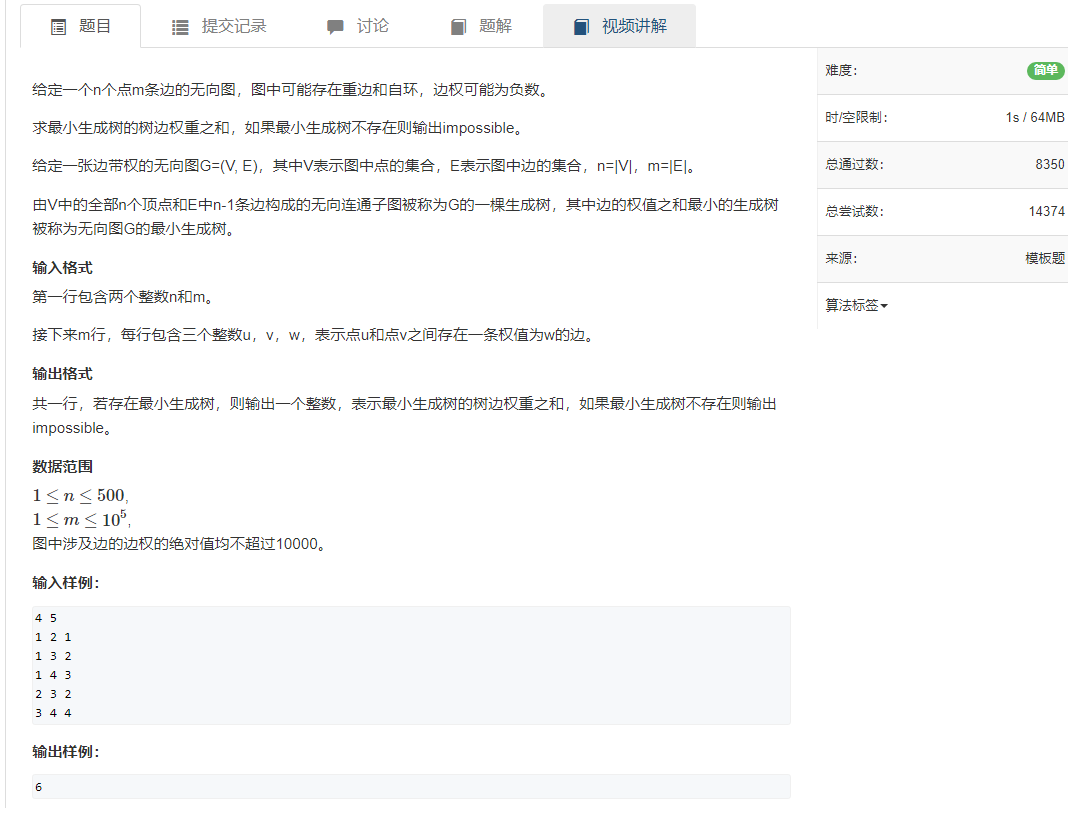
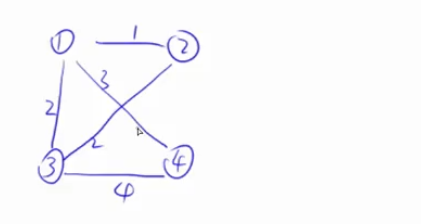
首先让所有点到集合的距离都是正无穷，然后找到一个集合外到集合距离最近的点，这四个点距离都是正无穷，我们则可以随便挑一个点

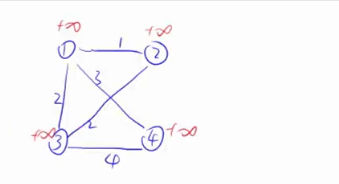
这里我们挑1号点，之后找到1号点到集合的最短距离，若该点没有边连到集合，则该点到集合的距离还是正无穷。

若找到了1号点到集合的最短距离，则用1号点去更新所有其它点到集合的距离

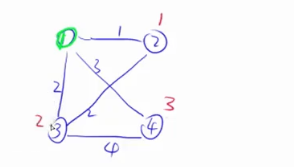
之后把1号点（绿点）加到集合当中去。

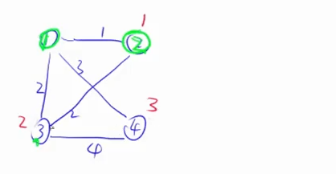
第二次迭代，从剩下的点当中选一个到集合距离最近的点，这里2号点最近，选中2号点之后，用2号点更新其它点到集合的距离（这个例子中更新前后结果不变，因为3到1和3到2的距离都是2，而且2和4没有连接），更新完之后，把2号点加到集合里面去。

重复进行上述操作，在3和4中找距离最近的点，这里3最近，用3更新4到集合的距离时，3到4的距离是4，比1到4的距离3要大，所以这里不更新。我们的目的是将距离更新的更短，距离如果变长，我们就不更新。

#define _CRT_SECURE_NO_WARNINGS
#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N= 510,INF=0x3f3f3f3f;
int n, m;
int g[N][N];//某俩点间的距离
int dist[N];//某点到集合的距离
bool st[N];
int prim()
{
    memset(dist, 0x3f, sizeof dist);
    int res = 0;//存储最小生成树所有边的长度之和
    for (int i = 0; i < n; ++i)
    {
        int t = -1;
        for (int j = 1; j <= n; j++)//找到集合外所有距离最小的点
        {
            if (!st[j] && (t == -1 || dist[t] > dist[j]))//t=-1表示当前还没有找到距离最小的点
                //如果t代表的点到集合的距离大于j代表的点到集合的距离，也表示当前没找到
                t = j;
        }
            if (i && dist[t] == INF)//说明当前距离最近的点到集合的距离是正无穷，即所有点没有连通
            {
                return INF;
            }
            if (i) res += dist[t];//dist[t]表示当前点和另一个点（该点已与集合连好）的距离
            for (int j = 1; j <=n; ++j)
            {
                dist[j] = min(dist[j], g[t][j]);//更新其它点
            }
        
            st[t] = true;//修改状态
        
    }
    return res;
}
int main()
{
    scanf("%d %d", &n, &m);
    memset(g, 0x3f, sizeof g);
    while (m--)//读入所有边
    {
        int a, b, c;
        scanf("%d %d %d", &a, &b, &c);
        g[a][b] = g[b][a]=min(g[a][b],c);//由于不用考虑边的正负，a到b的距离和b到a的距离都一样,因为可能有重边，我们取一个最小值
    }
    int t = prim();
    if (t == INF)//不存在生成树
        puts("impossible");
    else//存在生成树
        printf("%d", t);
    return 0;
}

克鲁斯卡尔算法

先将所有边按权重从小到大进行排序

枚举每条边a，b权重为c

如果当前a，b不连通，就把a，b这条边加到集合里面来

第二步其实是前面所学并查集的应用

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 200010;
int n, m;
int p[N];

struct Edge
{
    int a, b, w;//a,b是边的俩条点,w是权重
    bool operator<(const Edge& W) const//重载小于号方便排序
    {
        return w < W.w;
    }
}edges[N];
int find(int x)
{
    if (p[x] != x)//如果x不是祖宗节点
        p[x] = find(p[x]);
    return p[x];
}
int main()
{
    scanf("%d %d", &n, &m);
    for (int i = 0; i < m; ++i)
    {
        int a, b, w;
        scanf("%d %d %d", &a, &b, &w);//把所有的边读进来
        edges[i] = { a,b,w };
    }
    sort(edges, edges + m);//把所有的边排序
    for (int i = 1; i <=n; ++i)//初始化并查集
        p[i] = i;
    int res = 0, cnt = 0;//res存的是最小生成树当中所有树边的权重之和，cnt是当前加了多少条边
    for (int i = 0; i < m; ++i)//从小到大枚举所有边
    {
        int a = edges[i].a, b = edges[i].b, w = edges[i].w;
        a = find(a), b = find(b);//a=a的祖宗节点，b=b的祖宗节点，find函数是并查集的find函数
        if (a != b)//如果俩个祖宗节点不连通
        {
            p[a] = b;//这条边加进来之后，要把俩个点各自所在的集合进行合并
            res += w;
            cnt++;
        }
    }
    if (cnt < n - 1)//如果连的边数<n-1，说明这个树是不连通的
        puts("impossible");
    else
        printf("%d\n",res);
    return 0;
}

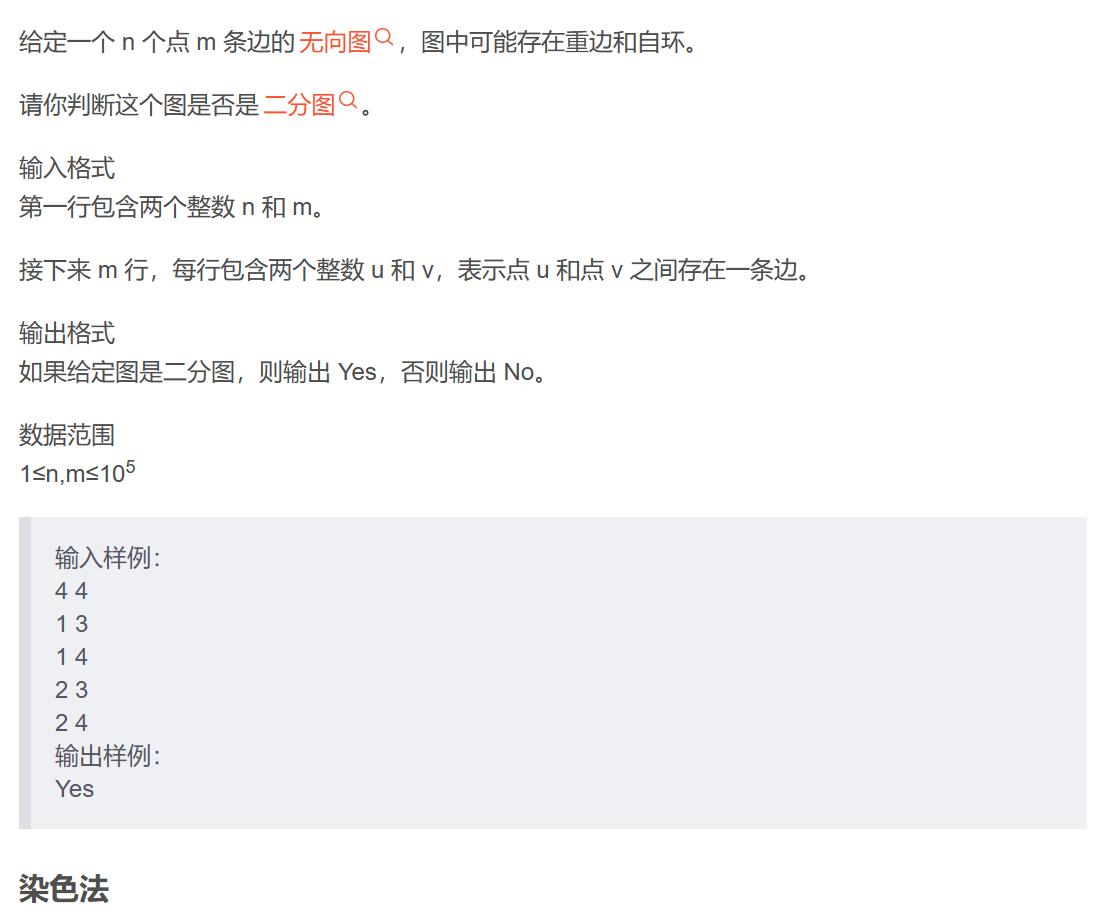
二分图

二分图定义：所有点划分到俩边区，使所有的边都是在集合之间的，集合内部没有边。如果一个图中有奇数环，则一定不是二分图。把图分为俩个区域，一个是左边，另一个是右边。

染色法

如果一个图中不含有奇数环则一定是二分图。

从前往后遍历每一个点

如果某个点还没分好组，我们就分到左边去

分完该点之后，遍历这个点和所有的邻点（和这个点连通的所有点），若该点属于左边，则它的所有相邻点属于右边，若该点属于右边，则它的所有相邻点属于左边，下图中第一个点属于左边，1代表左边，2代表右边，按照这种方式，将所有点可表示出来，其实就是在染色。

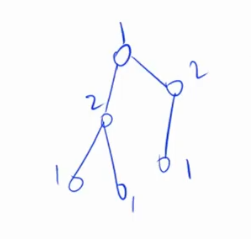
染色的时候要注意：一条边的俩端点的颜色，一定不同，即这俩个点不能属于同一个集合。通过这种方式将图中的所有点进行染色。由于图中不存在奇数环，所以染色过程中不会出现矛盾。

只要一个图可以用染色法染完，而且不出现矛盾，它就是一个二分图。

这里采用深度优先遍历进行染色。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 1010, M = 2010;//由于是无向图，每条无向边要存俩条有向边，即俩个点之间有俩条线,所以M是N的2倍
int n, m;
int h[N], e[M], ne[M], idx;
int color[N];
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool dfs(int u,int c)
{
    color[u] = c;//记录一下当前点颜色是C
    for (int i = h[u]; i != -1; i = ne[i])
    {
        int j = e[i];//存储当前点的编号
        if (!color[j])//如果当前点没有颜色
        {
            if (!dfs(j,3-c)) //如果当前是颜色1，就染成2，如果是颜色2，就染成1，这里写成3-c
                return false;//如果染色不成功就返回false,成功返回true
        }
        else if (color[j]==c)//如果这俩个相等，代表一条边的俩端点颜色一样，也有矛盾
        {
            return false;
        }
    }
    return true;
}
int main()
{
    scanf("%d %d", &n, &m);
    memset(h, -1, sizeof h);
    while (m--)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b);
        add(b, a);//由于是无向边，所以这里加俩条边，一条a到b，一条b到a

    }
    //开始染色
    bool flag = true;//标志位，表示染色成功或失败
    for(int i=1;i<=n;++i)
        if (!color[i])
        {
            if (!dfs(i, 1))//如果有矛盾dfs返回fasle,这里传1是想把有矛盾的地方染成第一种颜色，
            {
                flag = false;
                break;
            }
        }
    if (flag)
        puts("Yes");
    else
        puts("No");//有矛盾发生
    return 0;

}

匈牙利算法

假设有这样的一个二分图

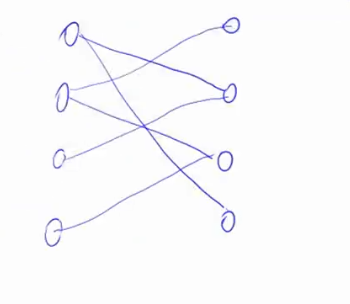
匈牙利算法可以在一个比较块的时间内，算出左边和右边最大的匹配成功（不存在俩条边共用一个点）数是多少。

1.如果a和b点已经匹配好了，c点要和b匹配，此时c点找一下有没有其它能和a匹配的点，如果有，就让a和其它点去匹配，然后c自己和b匹配。

#include<iostream>
#include<cstring>
#include<algorithm>
using namespace std;
const int N = 510, M = 100010;
int n1, n2, m;
int h[N], e[M], ne[M], idx;
int match[N];//右边对应的点
bool st[N];//右边的某点是否匹配成功
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx++;
}
bool find(int x)
{
    for (int i = h[x]; i != -1; i= ne[i])//遍历左边的点
    {
        int j = e[i];//当前左边点的编号
        if (!st[j])//如果当前右边的点还未匹配
        {
            st[j] = true;//进行匹配
            if (match[j] == 0||find(match[j]))//0表示还没匹配,或者说已经匹配到了左边的某点，但左边的这个点可以去匹配别的点
            {
                match[j] = x;
                return true;
            }
        }
    }
    return false;
}
int main()
{
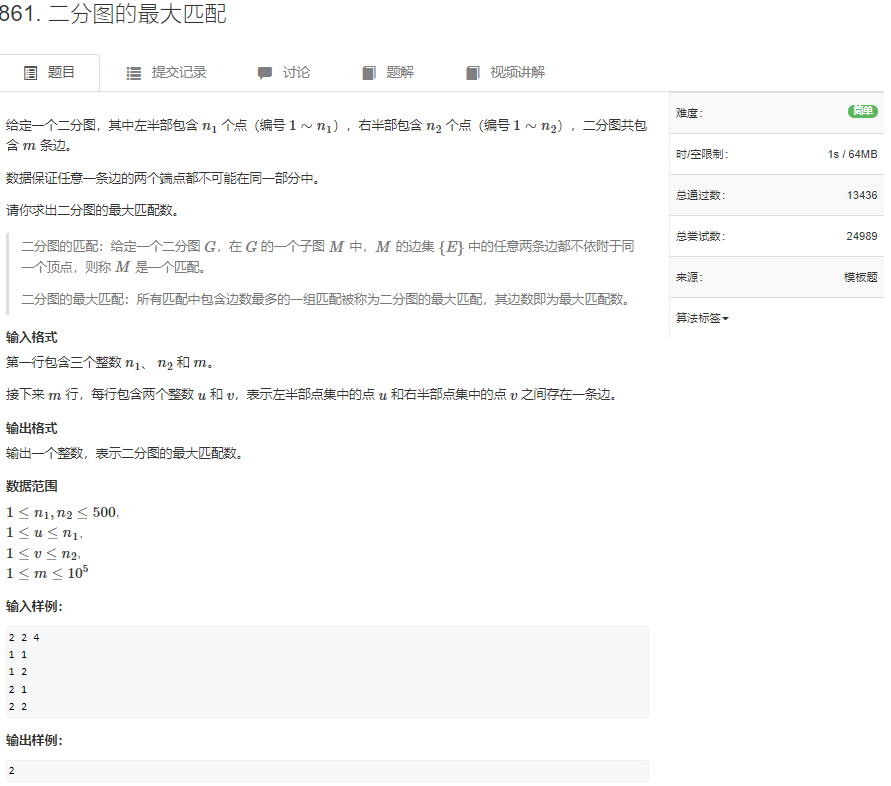
    scanf("%d %d %d", &n1, &n2, &m);
    memset(h, -1, sizeof h);
    while (m--)
    {
        int a, b;
        scanf("%d %d", &a, &b);
        add(a, b);
    }
    int res = 0;//当前匹配的数量
    for (int i = 1; i <= n1; ++i)
    {
        memset(st, false, sizeof st);
        if (find(i)) res++;//如果左边右边匹配成功，直接++
    }
    printf("%d\n", res);
    return 0;
}