Leetcode38. 外观数列

news2024/9/22 3:38:18

一、题目描述：

给定一个正整数 n ，输出外观数列的第 n 项。

「外观数列」是一个整数序列，从数字 1 开始，序列中的每一项都是对前一项的描述。

你可以将其视作是由递归公式定义的数字字符串序列：

countAndSay(1) = “1”
countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。

前五项如下：

1.     1
2.     11
3.     21
4.     1211
5.     111221
第一项是数字 1 
描述前一项，这个数是 1 即 “ 一 个 1 ”，记作 "11"
描述前一项，这个数是 11 即 “ 二 个 1 ” ，记作 "21"
描述前一项，这个数是 21 即 “ 一 个 2 + 一 个 1 ” ，记作 "1211"
描述前一项，这个数是 1211 即 “ 一 个 1 + 一 个 2 + 二 个 1 ” ，记作 "111221

要描述一个数字字符串，首先要将字符串分割为最小数量的组，每个组都由连续的最多相同字符组成。然后对于每个组，先描述字符的数量，然后描述字符，形成一个描述组。要将描述转换为数字字符串，先将每组中的字符数量用数字替换，再将所有描述组连接起来。

示例 1：
- 输入：n = 1
- 输出：“1”
- 解释：这是一个基本样例。
示例 2：
- 输入：n = 4
- 输出：“1211”
- 解释：
  - countAndSay(1) = “1”
  - countAndSay(2) = 读 “1” = 一个 1 = “11”
  - countAndSay(3) = 读 “11” = 二个 1 = “21”
  - countAndSay(4) = 读 “21” = 一个 2 + 一个 1 = “12” + “11” = “1211”

提示：
- 1 <= n <= 30

二、解决思路和代码

1. 解决思路

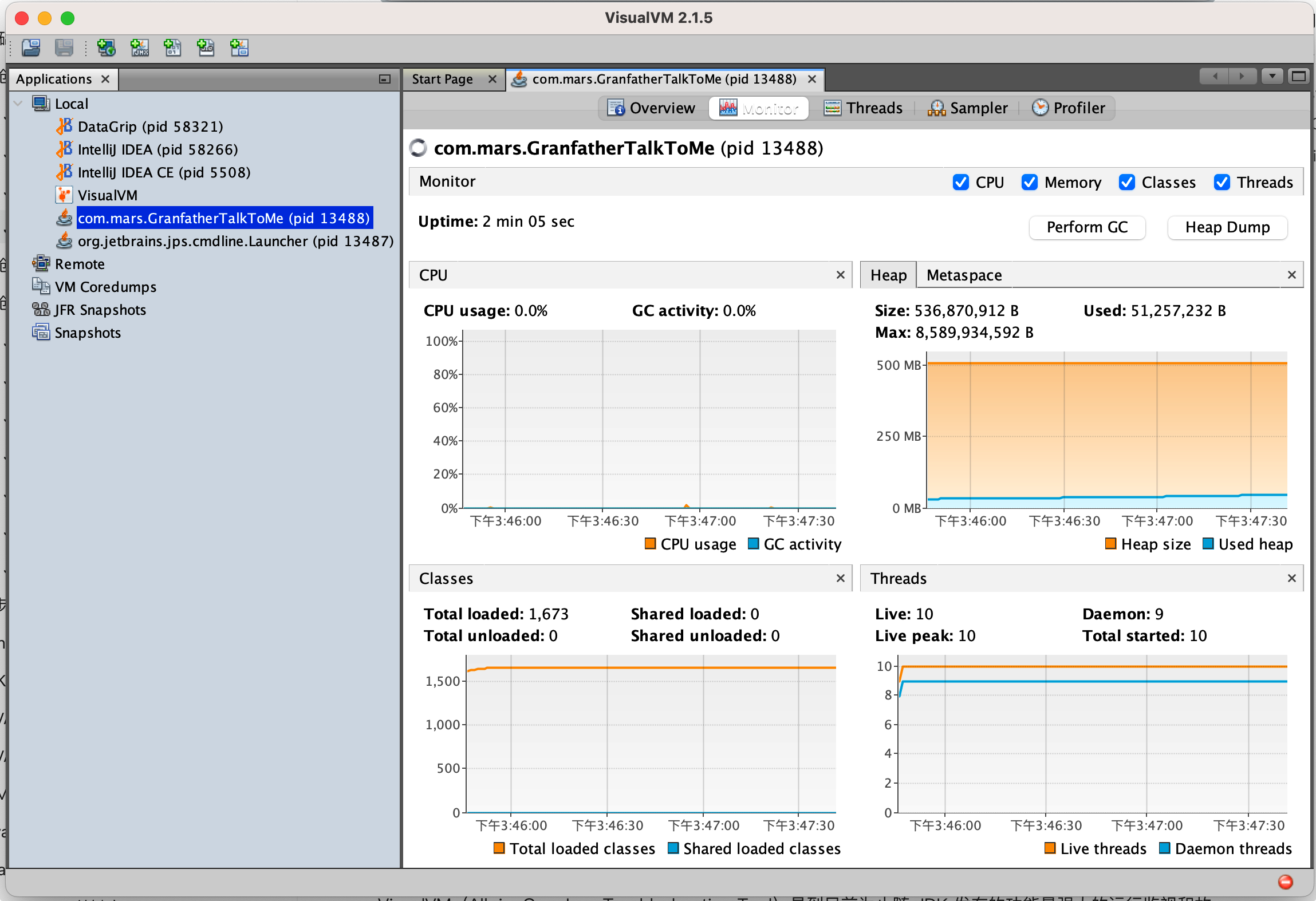
分析：可以使用递归的方法求解，也可以使用循环。下面讲一下使用for循环的思路。由于 countAndSay(n) 是对 countAndSay(n-1) 的描述，然后转换成另一个数字字符串。求 countAndSay(n) 要知道 countAndSay(n-1) 的结果，所以求countAndSay(n)的思路：countAndSay(1) -> countAndSay(2) -> … -> countAndSay(n)。求解第 k 项的思路是：
- countAndSay(k-1)=res, 借助两个指针：
  - numId：指向当前待描述的数字的索引
  - sameId：为统计当前待描述的数字相同的个数设置的指针或者是指向下一个【不同于当前待描述的数字res[numId]】待描述的数字。当遇到res[sameId]=res[numId]，sameId指针就向后移一位。

2. 代码

class Solution:
    def countAndSay(self, n: int) -> str:
        res = '1'
        start = 2
        while start<=n:
            temp = ''
            numId = sameId = 0
            while sameId<len(res):
                while sameId<len(res) and res[sameId]==res[numId]: sameId+=1
                temp += str(sameId-numId)+res[numId]
                numId = sameId
            res = temp
            start += 1
        return res