文章目录
- 不同路径
- 题解(动态规划)
- 数论方法
- [不同路径 II](https://leetcode.cn/problems/unique-paths-ii/description/)
- 题解
不同路径
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (67.70%) | 1746 | 0 | - | - | 0 |
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish” )。
问总共有多少条不同的路径?
示例 1:
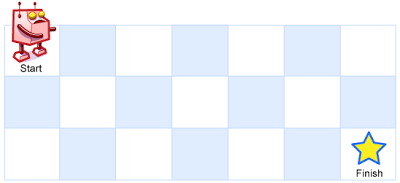
输入:m = 3, n = 7
输出:28
示例 2:
输入:m = 3, n = 2
输出:3
解释:
从左上角开始,总共有 3 条路径可以到达右下角。
1. 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右
3. 向下 -> 向右 -> 向下
示例 3:
输入:m = 7, n = 3
输出:28
示例 4:
输入:m = 3, n = 3
输出:6
提示:
1 <= m, n <= 100- 题目数据保证答案小于等于
2 * 109
Discussion | Solution
题解(动态规划)
class Solution {
public:
int uniquePaths(int m, int n) {
vector<vector<int>> dp(m,vector<int>(n,0));
for(int i = 0; i < m; ++i) dp[i][0] = 1;
for(int j = 0; j < n; ++j) dp[0][j] = 1;
for(int i = 1; i < m; ++i) {
for(int j = 1; j < n; ++j) {
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
- 时间复杂度:O(m × n)
- 空间复杂度:O(m × n)
数论方法
可以转化为,给你m + n - 2个不同的数,随便取m - 1个数,有几种取法。
class Solution {
public:
int uniquePaths(int m, int n) {
long long numerator = 1; // 分子
int denominator = m - 1; // 分母
int count = m - 1;
int t = m + n - 2;
while (count--) {
numerator *= (t--);
while (denominator != 0 && numerator % denominator == 0) {
numerator /= denominator;
denominator--;
}
}
return numerator;
}
};
- 时间复杂度:O(m)
- 空间复杂度:O(1)
不同路径 II
| Category | Difficulty | Likes | Dislikes | ContestSlug | ProblemIndex | Score |
|---|---|---|---|---|---|---|
| algorithms | Medium (41.00%) | 1032 | 0 | - | - | 0 |
数组 | 动态规划 | 矩阵
一个机器人位于一个 m x n 网格的左上角 (起始点在下图中标记为 “Start” )。
机器人每次只能向下或者向右移动一步。机器人试图达到网格的右下角(在下图中标记为 “Finish”)。
现在考虑网格中有障碍物。那么从左上角到右下角将会有多少条不同的路径?
网格中的障碍物和空位置分别用 1 和 0 来表示。
示例 1:

输入:obstacleGrid = [[0,0,0],[0,1,0],[0,0,0]]
输出:2
解释:3x3 网格的正中间有一个障碍物。
从左上角到右下角一共有 2 条不同的路径:
1. 向右 -> 向右 -> 向下 -> 向下
2. 向下 -> 向下 -> 向右 -> 向右
示例 2:

输入:obstacleGrid = [[0,1],[0,0]]
输出:1
提示:
m == obstacleGrid.lengthn == obstacleGrid[i].length1 <= m, n <= 100obstacleGrid[i][j]为0或1
Discussion | Solution
题解
// @lc code=start
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
int m = obstacleGrid.size();
int n = obstacleGrid[0].size();
if(obstacleGrid[m-1][n-1] == 1 || obstacleGrid[0][0] == 1) {
return 0;
}
vector<vector<int>> dp(m,vector<int>(n,0));
for(int i = 0; i < m &&obstacleGrid[i][0] == 0;++i) dp[i][0] = 1;
for(int j = 0; j < n &&obstacleGrid[0][j] == 0;++j) dp[0][j] = 1;
for(int i = 1; i < m; ++i) {
for(int j = 1;j < n;++j) {
if(obstacleGrid[i][j] == 1) continue;
dp[i][j] = dp[i-1][j] + dp[i][j-1];
}
}
return dp[m-1][n-1];
}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(n × m)
同样我们给出空间优化版本:
class Solution {
public:
int uniquePathsWithObstacles(vector<vector<int>>& obstacleGrid) {
if (obstacleGrid[0][0] == 1)
return 0;
vector<int> dp(obstacleGrid[0].size());
for (int j = 0; j < dp.size(); ++j)
if (obstacleGrid[0][j] == 1)
dp[j] = 0;
else if (j == 0)
dp[j] = 1;
else
dp[j] = dp[j-1];
for (int i = 1; i < obstacleGrid.size(); ++i)
for (int j = 0; j < dp.size(); ++j){
if (obstacleGrid[i][j] == 1)
dp[j] = 0;
else if (j != 0)
dp[j] = dp[j] + dp[j-1];
}
return dp.back();
}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
][j] == 1)
dp[j] = 0;
else if (j != 0)
dp[j] = dp[j] + dp[j-1];
}
return dp.back();
}
};
- 时间复杂度:O(n × m),n、m 分别为obstacleGrid 长度和宽度
- 空间复杂度:O(m)