梯度下降法

梯度下降法是一种常用的优化算法，用于求解目标函数的最小值。其基本思想是，通过不断地朝着函数梯度下降的方向更新参数，直到找到函数的最小值。

具体来说，假设我们有一个可导的目标函数 $f(x)$，我们要求它的最小值。首先，我们随机初始化一个参数向量 $x_0$，然后计算该点处的梯度 $g(x_0)=\nabla f(x_0)$。接着，我们沿着梯度的负方向更新参数，即 $x_1=x_0-\eta g(x_0)$，其中 $\eta$ 是学习率，它控制了每一步更新的幅度。然后，我们继续计算 $x_1$ 处的梯度，重复上述更新过程，直到找到目标函数的最小值。

梯度下降法有两种常用的变体：批量梯度下降法和随机梯度下降法。批量梯度下降法在每次更新参数时都要计算全部样本的梯度，因此它的计算开销比较大，但是更新方向比较稳定，收敛速度比较慢。随机梯度下降法在每次更新参数时只考虑一个样本的梯度，因此它的计算开销比较小，但是更新方向比较不稳定，收敛速度比较快。

梯度下降法的数学公式推导如下：

这里我们以批量梯度下降法为例：

import numpy as np
import matplotlib.pyplot as plt

# 生成样本数据
np.random.seed(0) 
X = np.random.rand(50, 1)
# 生成目标值
y = 2 * X + np.random.randn(50, 1) * 0.1

# 定义损失函数
def loss_function(X, y, w):
    m = len(y)
    J = 1 / (2 * m) * np.sum((X.dot(w) - y) ** 2)
    return J

# 定义梯度下降函数
def gradient_descent(X, y, w, alpha, num_iters):
    m = len(y)
    J_history = np.zeros((num_iters, 1))
    for i in range(num_iters):
        w = w - alpha / m * X.T.dot(X.dot(w) - y)
        J_history[i] = loss_function(X, y, w)
        print("Iteration {}, w = {}, loss = {}".format(i, w.ravel(), J_history[i, 0]))
    return w, J_history

# 初始化参数
w = np.zeros((2, 1))
alpha = 0.1
num_iters = 10000000

# 添加一列偏置项
X_b = np.c_[np.ones((len(X), 1)), X]

# 运行梯度下降算法
w, J_history = gradient_descent(X_b, y, w, alpha, num_iters)

# 输出最终的参数值和损失函数值
print("Final parameters: w = {}, loss = {}".format(w.ravel(), J_history[-1, 0]))

# 绘制样本数据散点图
plt.scatter(X, y, alpha=0.5)

# 生成拟合直线的点坐标
x_line = np.array([[0], [1]])
y_line = x_line * w[1, 0] + w[0, 0]

# 绘制拟合直线
plt.plot(x_line, y_line, color='r')

# 显示图像
plt.show()

在Jupyter里面运行之后我们发现输出如下：

Output exceeds the size limit. Open the full output data in a text editorIteration 0, w = [0.10586793 0.07155122], loss = 0.5557491892500293
Iteration 1, w = [0.19729987 0.13480597], loss = 0.44015806935473656
Iteration 2, w = [0.27618572 0.19084247], loss = 0.3525877150650007
Iteration 3, w = [0.34416842 0.24059807], loss = 0.28619553470776754
Iteration 4, w = [0.40267618 0.28488764], loss = 0.23581044813963176
Iteration 5, w = [0.45295053 0.32441962], loss = 0.19752456266928253
Iteration 6, w = [0.49607077 0.35980988], loss = 0.16838459622747565
Iteration 7, w = [0.53297511 0.39159387], loss = 0.1461586810761424
Iteration 8, w = [0.56447915 0.42023707], loss = 0.12916013375789542
Iteration 9, w = [0.59129188 0.44614419], loss = 0.11611427531530936
Iteration 10, w = [0.61402962 0.46966706], loss = 0.10605778526555067
Iteration 11, w = [0.63322814 0.49111157], loss = 0.09826264183760337
Iteration 12, w = [0.64935317 0.51074369], loss = 0.09217864242878422
Iteration 13, w = [0.66280956 0.52879465], loss = 0.08738996542064487
Iteration 14, w = [0.67394923 0.54546548], loss = 0.08358234326756732
Iteration 15, w = [0.6830781  0.56093099], loss = 0.0805182546884386
Iteration 16, w = [0.69046209 0.57534318], loss = 0.07801817701869833
Iteration 17, w = [0.69633236 0.5888342 ], loss = 0.07594641831943069
Iteration 18, w = [0.70088983 0.60151897], loss = 0.07420041047978741
Iteration 19, w = [0.70430916 0.61349743], loss = 0.07270261784568362
Iteration 20, w = [0.70674215 0.62485649], loss = 0.07139442244222281
Iteration 21, w = [0.70832077 0.63567171], loss = 0.07023150293863561
Iteration 22, w = [0.70915971 0.64600884], loss = 0.06918034245759412
Iteration 23, w = [0.70935865 0.65592505], loss = 0.0682155894697291
Iteration 24, w = [0.70900424 0.66547007], loss = 0.06731806337787473
...
Iteration 999997, w = [-7.21008413e-04  1.96927329e+00], loss = 0.004277637843402933
Iteration 999998, w = [-7.21008413e-04  1.96927329e+00], loss = 0.004277637843402933
Iteration 999999, w = [-7.21008413e-04  1.96927329e+00], loss = 0.004277637843402933
Final parameters: w = [-7.21008413e-04  1.96927329e+00], loss = 0.004277637843402933

可以看到我们这里是迭代了100万次，它的loss已经下降到了千分之四的水平
得益于较低的loss率，我们可以看到线性回归的图像表现比较良好。

给定训练集 $(x^{(1)},y^{(1)}),(x^{(2)},y^{(2)}),\cdots ,(x^{(m)},y^{(m)})$，其中 $x^{(i)}\in {\mathbb{R}}^{n+1}$，$y^{(i)}\in \mathbb{R}$，$i=1,2,\cdots ,m$，假设 $y^{(i)}$ 与 $x^{(i)}$ 满足如下关系：

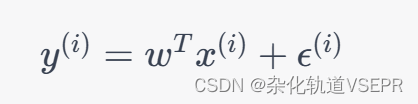
其中 $w\in {\mathbb{R}}^{n+1}$ 是待求解的参数，${ϵ}^{(i)}$ 是噪声项。我们的目标是找到一个 $w$ 使得训练集上的损失函数最小：

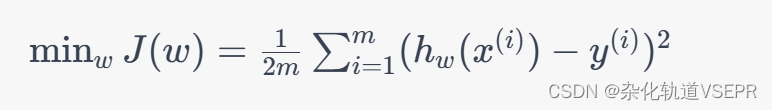
其中 $h_w(x)=w^{T}x$ 是预测函数，$m$ 是训练集的大小。
使用梯度批量下降法求解 $w$，更新公式为：

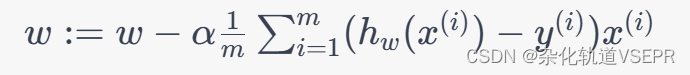
其中 $\alpha$ 是学习率，$m$ 是批量大小。